СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О СТРОЕНИИ РАБОЧЕГО СЛОЯ АБРАЗИВНЫХ ИНСТРУМЕНТОВ

В данной главе приведен краткий обзор работ советских и зарубежных авторов по рассматриваемому вопросу. Системати­зация этих работ, в которых даны методика исследования и мате­матическая интерпретация экспериментальных данных, позволит судить о состоянии вопроса в целом.

Рассматриваемые работы посвящены описанию микрорельефа поверхности шлифовальных кругов с использованием аппарата теории вероятности и математической статистики в случае круглого шлифования (высокие скорости резания), хонингования (средние скорости резания) и доводки свободным абразивом (малые скорости резания).

Микрорельеф поверхности круга изучается в зависимости от методов правки и режимов шлифования, зернистости и концен­трации абразивных зерен на статических и динамических моделях с отражением реальных условий шлифования.

Сравнивая эти работы, можно увидеть позитивные стороны установившейся практики анализа взаимодействия PC шлифоваль­ных инструментов с обрабатываемыми материалами, а также не­достатки методических приемов и упрощений, допускаемых при изучении процессов таких взаимодействий.

А. Н. Резников [73—75] при исследовании вопросов теплофи­зики шлифования исходил из законов случайного распределения зерен эллипсовидной формы в ПС абразивных инструментов.

Закон распределения размеров зерен в круге принимается им аналогичным закону (1.3), но отличается от последнего центром группирования и среднеквадратичным отклонением в связи с изме­нением зернового состава круга в процессе прессования по сравнению с зерновым составом исходного порошка:

В процессе изготовления любое зерно из алмазного порошка может оказаться в любом месте алмазоносного слоя инструмента, т. е. расположение данного зерна на том или ином расстоянии по отношению к рабочей поверхности круга имеет одну и ту же веро­ятность.

Если обозначить через а0 соотношение между площадями се­чения зерна и площадью круга, проведенного через наибольший размер этого сечения как через диаметр (по измерениям а„ да да 0,5 0,6), малая полуось эллипса, к которому приведены кон­

туры сечения зерна, будет равна а = а0х, так как аш = су, [см. формулы (1.1) и (1.2)].

Концентрация алмазов в круге может быть выражена через соотношение

Если объем алмазов тш составляет V4 объема алмазоносного слоя круга w, то, как следует из формулы, концентрация, /(=100%.

Общее количество зерен всех размеров в единице объема алмазо­носного слоя круга определяется сопоставлением двух выражений — через закон распределения (формула 3.1) и через концентрацию

Здесь N — общее количество зерен в круге; функция под инте­гралом — закон распределения объемов зерен.

Поскольку появление зерен за пределами ±3^ от центра груп­пирования имеет малую вероятность, можно перейти к пределам

—со и +оо. Учитывая выра­жение w (х) по формуле (1.1) и вычисляя интеграл, А. Н. Рез­ников получает

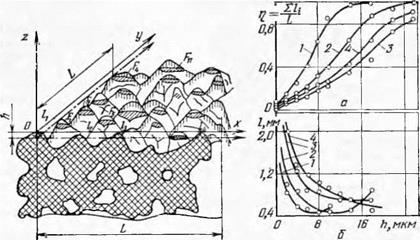
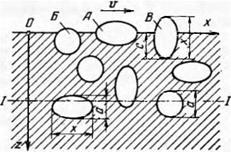
Для расчета количества зе­рен, располагающихся на еди­нице рабочей поверхности кру — Рис. 44. Схематизация расположения зе — га> определяется вероятность рен в круге. пересечения зерен любой по­

верхностью (плоскостью), эк­видистантной рабочей поверхности (плоскости круга).

Для упрощения расчетов А. Н. Резников принимает три вида расположения зерен на высоте алмазоносного слоя (рис. 44): параллельно оси х (тип А), параллельно оси у (тип Б) и параллельно оси z (тип В). Появление зерен любого типа равновероятно, т. е. вероятность появления каждого из них равна Vs.

Вероятность того, что любая плоскость I—/, в том числе и рабочая поверхность круга, пересечет зерно типа А, размер которого находится в пределах от х до х + Ах, определяется произведением

трех вероятностей: | х ^ х 1/ W <Д. Первая определяет вероят — 124

ность того, что зерно окажется типа А; вторая — вероятность того, что зерно, имеющее малую ось размером а, расположенное в алма­зоносном слое толщиной h, будет пересечено данной плоскостью; третья — вероятность наличия в круге зерен, большая ось которых имеет размер от х до х + dx.

Для всех зерен, размер которых находится в пределах от х

до х -f — dx, вероятность пересечения будет равна ^ + — g — X

X у (x)dx. Для всех зерен, размер которых находится в пределах от Xmi„ ДО Хтах (уСЛОВИе ОТ — ОО ДО + оо), ВерОЯТНОСТЬ ПЄрЄСЄЧЄНИЯ рабочей поверхностью круга равна

=

Общее номинальное количество зерен, располагающихся на 1 мм2 рабочей поверхности,

где 5 — площадь рабочей поверхности круга.

После подстановки значения nw по (3.4) и а„= | аш, а также ре­шения интеграла для Р0

где п0 — номинальное количество зерен, располагающихся в сред­нем на 1 мм2 рабочей поверхности круга; дг, — центр группирова­ния зерен различных размеров в порошке, который связан с номинальным (паспортным) размером зерна хн ; хх = 6jXH; о — среднеквадратическое отклонение размеров зерен о = с^х„.

Подставляя значения х1 и о в формулу (3.5), можно получить

(2«0 + 1) А
200лашх2 (с2 + 3ф

Для алмазных кругов на основании экспериментов и обработки литературных данных ориентировочно принято сх ~ 0,77; сг ~ » 0,105; а0 = 0,6; аш = 0,36 и

(3-7)

В связи с неизбежной потерей зерен из-за шлифования и правки фактическое количество зерен на поверхности круга будет меньше номинального п0.

Зерно данного размера х может размещаться по высоте как угодно по отношению к любой поверхности. Следовательно, любое значение глубины заделки зерна сд в пределах размера а (для зерен типа А) имеет одну и ту же вероятность. Аналогично равновероятна
глубина заделки св в пределах размера а (для зерен типа Б) и глу­бина заделки с в в пределах размера х (для зерен типа В). Обозначив через ех отношение глубины заделки зерна к его размеру по высоте в направлении, перпендикулярном к рабочей поверхности круга, можно получить для зерен типов А, Б, С соответственно

Величины еа, єб и ёв одновременно равны вероятностям появ­ления зерен, имеющих заделку не более чем Са, Сб, Св. При некото­ром критическом значении ек зерно не может удерживаться в PC круга. Следовательно, все зерна, например типа А, для которых в данный момент времени еа < ек, выкрошатся и покинут круг.

Вероятность того, что одновременно произойдут четыре события: зерно будет типа А; оно будет пересечено рабочей поверхностью круга; это зерно будет иметь заделку, меньшую или равную крити­ческой ек; размер зерна будет находиться в пределах от х до х + dx, может быть рассчитана по формуле вероятности совместных событий

Рассчитывая далее аналогично элементарные вероятности для зерен типов Б и В, суммируя эти вероятности и интегрируя в пре­делах от— оо до +оо, получаем возможность рассчитать вероятность и общее количество зерен, покинувших круг на 1 мм2 его рабочей поверхности:

откуда п„ = п0ек.

Количество оставшихся зерен и видимых на 1 мм2 рабочей по­верхности круга

По данным Д. Н. Резникова, ек = 0,2 ч — 0,7. Меньшие значения наблюдаются для меньших зернистостей и на металлической связке, большие — для крупных зерен на бакелитовой связке.

Практически значение ек определяют, сравнивая значение п„, рассчитанное по формулам (3.6) или (3.7), со средним количеством зерен, видимых на 1 мм2 поверхности круга при рассмотрении ее под микроскопом.

В резании будет участвовать еще меньшее, чем пв, количество зерен, так как вершины зерен расположены на различном расстоя­нии от наружной поверхности круга и только часть зерен попадает в слой, ограниченный глубиной резания.

Если провести наружную поверхность круга через наиболее выступающее зерно (рис. 45 — зерно типа В размером хтах), то наибольший вылет определяется коэффициентом Ej, так как зерна, имеющие вылет больший, чем Ащах = (1 — Єі)Хтах, ПОКИНуТ Круг.

Вершины всех остальных зерен, как показано на рис. 45, рас­положатся между А = О И А = Атах.

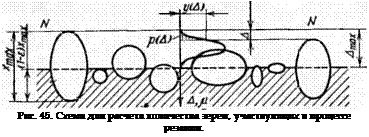Размер А определяется, по-видимому, случайными причинами. Поэтому распределение у (А) от 0 до Атах с достаточной надеж­ностью можно описать кривой нормального распределения со сред-

неквадратичным отклонением а0 =» —g— и центром группирования А

Вероятное количество вершин зерен, располагающихся от А = 0 до

На рис. 46 приведены значения функции Р (А) в зависимости от отношения А/Дтах, а на рис. 47 — кривые, полученные Л. И. Граб- ченко, изучавшим экспериментальным путем [30] частоту появле­ния зерен по глубине их залегания А от наружной поверхности кругов. Далее в работе [74] указывается, что идентичность кривых, приведенных на рис. 46 и 47, очевидна. Она будет еще нагляднее, если кривые, полученные экспериментальным путем, привести к безразмерному виду, как это сделано для закона размещения зерен АСОб (кривая 3 на рис. 47).

Вместе с тем кривые, полученные экспериментальным путем, отличаются от теоретической кривой в области значений А/Атах, близких к нулю. Опыт показывает, что на наружной поверхности располагается некоторое количество зерен, в связи с чем эксперимен­тальная кривая г (А) несколько смещена влево в системе координат г (А) = / (А/Атах)- Такое смещение вполне закономерно, так как теоретическая кривая Р (А) рассчитана для идеальной поверхности, проходящей через вершины идеализированных зерен, тогда как
экспериментальная кривая учитывает, что вершины зерен скалы­ваются и, следовательно, фактическая наружная поверхность рас­полагается ниже расчетной.

Если не учитывать смещение кривой Р (Д) влево, то при малых глубинах шлифования t можно допустить погрешность в определении Р (А) (в 2—3 раза), а это приведет к неправильному представлению о количестве активно работающих зерен.

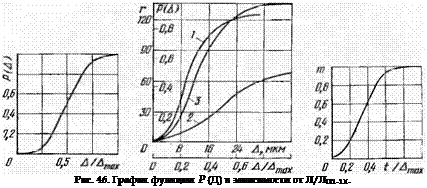Сдвинув теоретическую кривую Р (А) влево так, чтобы при А/Лпюх ее ордината составляла примерно 2% полного значения A/Ama* = 1, можно получить кривую, представленную на рис. 48.

Рис. 47. Экспериментальные данные о частоте появления вершинок зерен г в за­висимости от глубины залегания от наружной поверхности алмазного круга Д: 1 — АС06, К = 200%; 2 — АС025, К = 200%; 3 — АС06. К = 200%; в безразмерном

виде Р (Д) к ) (Д/ДПШХ)

Рис. 48. График для расчета вероятного количества зерен шлифовального круга,

участвующих в резании.

Здесь по оси абсцисс отложено отношение глубины резания t к расчетному значению Атах, по оси ординат — относительное ко­личество активных зерен в общем количестве п.

Количество режущих зерен на каждом 1 мм2 поверхности круга

Значения пр могут быть определены и другими путями, в част­ности экспериментальным. Так, например, по данным С. Г. Редько 171 ], количество рабочих зерен составляет пр = (0,1 — 0,12) п0. Эксперименты по определению пр позволяют скорректировать рас­

четные методы (в том числе и теоретико-вероятностный) определе­ния количества зерен, активно участвующих в резании.

С. А. Попов [67, 70] провел исследование по изучению рельефа режущей поверхности абразивных инструментов из синтетических алмазов и КНБ, а в соавторстве с Л. С. Соколовой [70] — изучение рельефа шлифовальных кругов из электрокорунда, отличающихся содержанием основной фракции и формой абразивных зерен.

Для оценки геометрии рельефа поверхности кругов был исполь­зован метод профилографирования [69] алмазной иглой с радиусом округления 10 мкм, углом при вершине 55° (игла отличалась от

Рис. 49. Рельеф режущей поверхности абразивного инструмента. Рис. 50. Изменение коэффициента длины контактной линии профиля (а) и сред, него шага между неровностями (б) по высоте рельефа алмазных кругов на метал­лической связке М5 с алмазами разных марок зернистостью 100/80: / — АСО: 2 — АСР; 3 — АСВ: 4-А.

стандартных игл меньшим значением угла при вершине конуса, что позволяло зафиксировать большее количество элементов рельефа). При обработке профилограмм базовая длина измерений прини­малась 80 мм. Горизонтальное увеличение было 135, вертикальное ■— 1800, что позволяло исследовать верхнюю часть профиля с глубиной до 50 мкм.

Высота рельефа в отдельных точках режущей поверхности является случайной функцией двух координат выбранной точки плоскости, касательной к номинальной поверхности абразивного инструмента (рис. 49)

Статистические параметры случайного однородного поля можно вычислить для одной реализации при достаточно большой площади поля. Вместо средних параметров по площади достаточно рассматри­вать средние значения по какому-либо сечению поля (профиль поля), например вдоль оси х.

Кривую профиля рельефа поверхности, отражающую зависимость высоты неровностей профиля от абсциссы профиля, можно рассмат­ривать как реализацию случайного процесса. Это позволяет про­извести вероятностный расчет суммарной длины 2/(- кусков, вы­резанных профилем на горизонтальной прямой на высоте Z над средней линией профиля. Величина 2/(- есть сумма многих случай­ных кусочков, и при достаточно длинной трассе, на которой умеща­ется несколько десятков гребней, можно указать пределы, в которых с заданной надежностью лежат значения 2/,-. Экспериментальное исследование рельефа методом профилографирования режущей поверхности алмазной иглой впервые было выполнено в 1956— 1958 гг.

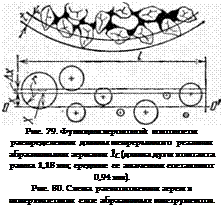
На рис. 50 показаны кривые изменения коэффициента длины контактной линии профиля и среднего шага между неровностями (зернами) по высоте рельефа алмазных кругов на связке М5 с ал­мазами разных марок: синтетическими АСО, АСР, АСВ и природ­ными А зернистостью 100/80. Поверхность кругов профилографиро — валась в опыте непосредственно после правки абразивным кругом из карбида кремния зеленого по методу шлифования.

Анализ профилограмм показал, что углубление средней кон­тактной поверхности рельефа, представляющее собой расстояние между базовой линией выступов зерен и средней контактной лини­ей профиля, составило 7 мкм для АСО, 12 мкм для АСР, 17 мкм для АСВ, 15 мкм для А.

Влияние марки алмазов сказалось и на геометрии отдельных зе­рен (радиусов округления вершин, углов между гранями и ребрами зерен, степени заглубления их в матрице связующего).

На рис. 51 показаны многоугольники распределения высоты вы­ступания зерна из матрицы (разность уровней между его вер­шиной и предшествующей ложбиной в связке), а на рис. 52 — рель­еф поверхности алмазных кругов на бакелитовой связке Б156. Харак­тер зависимостей такой же, как и для кругов с металлической связкой, однако количественные значения параметров здесь иные. Распреде­ление высоты выступания зерен над бакелитовой связкой в меньшей степени зависит от прочности зерен. Такое различие в распределении высоты выступания зерен связано не только с хрупкостью или проч­ностью зерен, но и с физико-механическими свойствами связующего: хрупкие зерна, закрепленные в металлической матрице при правке, разрушаются больше, чем в бакелитовой связке.

При применении бакелитовой связки с металлическими и мине­ральными наполнителями (связка Б156) хрупкие алмазы марки АСО часто оказываются эффективнее более прочных зерен других марок. Уменьшение контактной поверхности рельефа и увеличение среднего расстояния между зернами на поверхности кругов с ал­мазами разных марок связано с различием в удельной поверхности зерен.

Зерна с меньшей удельной поверхностью слабее удерживаются в ПС связующего, и значительная часть их выпадает при правке режущей поверхности инструмента. Эксплуатационные свойства инструмента в значительной мере зависят от его возможности ав­томатически поддерживать режущую способность на определенном уровне, т. е. обусловливаются механизмом саморегулирования рель­ефа режущей поверхности.

Процесс саморегулирования рельефа зависит не только от потенциальных свойств, сохраненных инструментом при его из-

Рис. 51. Многоугольники распределения высоты выступания зерен над связую­щим на поверхности алмазных кругов на металлической М5 (а) и бакелитовой Б156 (б) связках с алмазами разных марок: / — ACO; 2 — АСР: 3 — АСВ; 4 — А Рис. 52. Изменение коэффициента длины контактной линии профиля (а) и среднего шага между неровностями (б) по высоте рельефа алмазных кругов на бакелитовой связке Б156 с синтетическими алмазами разных марок зернистостью 125/100: / — ACO: 2 — АСР; 3 — АСВ.

готовлений, он связан также с условиями работы: обрабатывае­мый материал, технологическая среда, режимные факторы, обору­дование и т. д.

У кругов на прочных связках (например, бронзовых) процесс саморегулирования рельефа наблюдается только на протяжении неко­торого времени после правки, а затем преобладает постепенное сгла­живание рельефа. В табл. 12 приведены данные об изменении релье­фа поверхности круга с алмазами АСВ 120/100-М1-100% в процессе шлифования твердого сплава Т15К6 на следующем режиме: попереч­ная подача 0,04 мм/дв. хода, продольная подача 2 м/мин, скорость круга 18 м/сек. Вследствие сглаживания рельефа и увеличения контактной площади коэффициент режущей способности круга сни­зился в ходе опыта с 41 до 25 мм3/мин — кг, что сопровождалось повышением силы резания почти в 2,9 раза. Отношение тангенци-

Изменение рельефа поверхности круга в процессе
шлифования твердого сплава

	0	<	8	И	18	22
0 (правка)	0,02	0,10	0,17	0,36	0,60	0,77
00	0,02	0,09	0,12	0,23	0,33	0,52
120	0,02	0,07	0,17	0,32	0,45	0,62
240	0,01	0,14	0,26	0,51	0,74	0,93

Коэффициент длины контактной линии профиля при разном

Съем твердо — углублении секущей прямой, мкм го сплава, г_____________________________________________________ ______________________________________

альной составляющей силы резания к нормальной — коэффициент трения — царапания — возрос с 0,35 до 045.

Изменение рельефа зависит от физико-механических свойств обрабатываемого материала. На рис. 53 показано изменение коэффи­циента длины контактной линии профиля круга АСВ 100/80 непо­средственно после правки по методу шлифования и после сошлифо- вывания 150 г разных материалов: твердого сплава Т15К.6, стали 45 и совместно твердого сплава и стали 45. Режимы шлифования были постоянными: скорость круга 25 м/сек, продольная подача 2 м/мин, поперечная — 0,02 мм/дв. хода. При шлифовании твердого сплава происходит значительное заглаживание рельефа, при шлифовании стали 45 — истирание связующей матрицы. Удельный расход алмазов в условиях эксперимента составлял для сплава Т15К6 0,52 мг/г, для стали 45 3,7 мг/г, для сплава Т15К6 + сталь 45 94 мг/г. Интересно отметить, что сила резания не оставалась по­стоянной. Например, нормальная составляющая силы резания за период съема 340 г твердого сплава увеличилась с 4 до 7,8 кГ; за период шлифования стали 45 она снизилась с 8 до 6 кГ, а при совместной обработке сила резания колебалась около среднего значения, равного 6,5 кГ.

Изменение зернистости алмазных кругов от 125/100 до 63/50 часто не оказывает значительного влияния на рельеф круга и его контактную поверхность. Однако, если сравнивать зернистости в более широком диапазоне, то можно увидеть, что различие в рельефе поверхности становится значительным (это проявляется при шлифо­вании). Установлено, что круги, обладающие большей поверхно­стной пористостью, имеют более высокие режущие свойства, а мелко­зернистые круги с малой высотой выступания зерен из связки обес­печивают меньшую шероховатость поверхности.

Наблюдаемые явления связаны не только с величиной зерна. Они в значительной мере обусловлены толщиной слоя связующего между отдельными зернами. О толщине мостиков связки можно судить, если рассмотреть идеализированную модель расположения зерен со средним диаметром d в матрице по схеме гранецентриро-

ванного куба. В этом случае минимальная толщина С межзеренно — го слоя определяется формулой

C = d(|/-^~1), (3.13)

где V в — объемная доля абразивных зерен в матрице; d — средний диаметр зерна, идеализированного в виде шара.

При увеличении концентрации алмазов и уменьшении зернис­тости уменьшается толщина мостиков связки. При переходе от 50% — ной к 200%-ной концентрации алмазов толщина мостиков связки уменьшается в 5,8 раза, а объемное содержание алмазов возрастает в 4 раза (с 0,125 до 0,5). Это отражается на рельефе поверхности.

Рис. 53. Изменение коэффициента длины контактной линии профиля кру­га АСВ 100/80 на металлической связке М5-8 после правки (1) и шлифо­вания твердого сплава Т15К6 (2), стали 45 (3) и Т15К6 + сталь 45 (4) (вы­сота пластинок 1 : 0,5). Рис. 54. Изменение коэффициента длины контактной линии профиля по высоте рельефа поверхности эльборового круга Л 125/100 (Л 16) на связ­ке КБ после правки (1) и шлифования стали Р18 (2); стали ШХ15 (3); стали 45 (4); сплава Т15К6 (5); сплава Т15К6 + сталь 45 (6).

Так, для круга зернистостью АСВ 100/80 на связке М5-5 средний шаг между зернами на фиксированном уровне 4 мкм, отсчитываемом от уровня наиболее выступающих зерен при концентрации алмазов 50, 100, 150, 200% соответственно составлял 1,60 1,28, 0,85 0,67.

Значение измеренного среднего шага между активными элемен­тами зерен, расположенньми на верхних уровнях рельефа, в 5—10 раз больше тех значений, которые приводятся некоторыми исследо­вателями, отождествляющими расположение зерен в объеме мат­рицы с расположением зерен на поверхности круга.

На рис. 54 показано изменение рельефа поверхности эльборового круга Л 125/100 (Л16) на связке КБ после правки и шлифования различных металлов.

Различие в режущих свойствах и износостойкости связано с механическими свойствами зерен эльбора: алмазные зерна более стойки к излому и хрупкому разрушению, чем зерна эльбора. При правке эльборового круга по методу шлифования абразивным кру­гом происходит интенсивное заглаживание режущих элементов •зерен вследствие их хрупкого разрушения (рис. 54, кривая 1). Ана­логичные явления наблюдаются при обработке твердого сплава, керамики, твердого сплава со стальной подложкой (кривые 5, 6).

При обработке стали рельеф абразивной поверхности суще­ственно меняется: режущие зерна выступают из связки, фактическая контактная поверхность круга уменьшается, а углубление средней контактной поверхности увеличивается более чем в 2,5 раза.

Подобное саморегулирование рельефа связано с физико-меха­ническими свойствами эльбора, с характером хрупкого разрушения

Таблица 13 Характеристика рельефа поверхности абразивных кругов из неизометричных и изометричных зерэн *ср* ММ О О S п Изомет Неизомет- Пластин- Изомет- Неизомет- Пластин- Е Ф К ричное ричное ричное ричное чато-иголь- зерно зерно эерно зерно зерно чатое іерно 5 0,04 0,05 0,06 1,50 1,45 0,95 10 0,07 0,07 0,10 1,35 1,30 0,85 15 0,09 0,10 0,13 1,30 1,20 0,80 20 0,11 0,11 0,16 1,20 1,15 0,78 25 0,13 0,13 0,18 1,15 1,10 0,72 ЗО 0,15 0,15 0,20 1,10 1,05 0,70 40 0,18 0,18 0,24 1,05 1,00 0,60 50 0,21 0,21 0,28 1.00 1,00 0,55

зерен, прочностью соединения с матрицей связующего и взаимо­действием их с обрабатываемым материалом.

Для выявления влияния формы абразивного зерна на рельеф режущей поверхности кругов было проведено разделение на вибро­плоскости исходного зерна белого электрокорунда зернистостью № 40 по форме. Были выбраны три группы зерен: изометричные, неизометричные и пластинчато-игольчатые. Из этих зерен изготов­лены абразивные круги ЭБ40СМ1К5. Содержание основной фракции зерен в кругах составляло 50—60%.

Рельеф режущей поверхности кругов ЭБ40СМ1К5 из различных по форме групп зерен после правки их алмазным карандашом харак­теризовался параметрами, приведенными в табл 13, из которой видно, что существенной разницы в рельефе поверхности кругов из неизометричных и изометричных зерен не обнаружено. Рельеф кругов с пластинчато-игольчатыми зернами отличается большей контактной площадью на определенном уровне и меньшими средни­ми шагами между зернами.

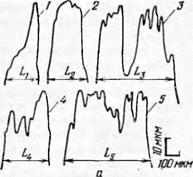
Анализ профилограмм рельефа поверхности кругов показал, что профиль отдельных зерен не является однотипным. Наиболее характерные формы профилей отдельных зерен представлены на рис. 55, а. Профили 1 и 2 можно рассматривать как одновершинные с разной величиной радиуса округления вершины; профили 3, 4

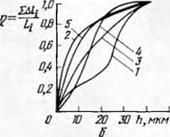и 5 имеют на активных элементах зерен по несколько вершин раз­ной высоты и степени округления граней и ребер. Это отражается на изменении относительной контактной площади по мере внедрения зерен в обрабатываемый материал (рис. 55, б).

Рис. 55. Геометрия абразивных зерен на режущей поверхности шлифо-
вального круга ЭБ40СМ1К5:

а — профили отдельных абразивных зерен (L£- — базовая/длина профилей зерен /,

2, 3, 4 и 5); 6 — кривые изменения коэффициента длины контактной линии про-
филя зерен от их высоты.

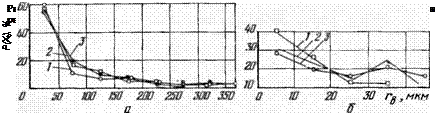
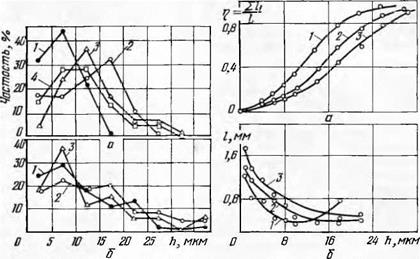
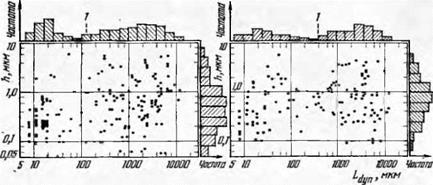
На рис. 56 приведены эмпирические кривые распределения ра­диусов округления вершин зерен на режущей поверхности шлифо­вальных кругов ЭБ40СМ1К5 из зерен различной формы. Около 55— 60% зерен имеют радиусы округления вершин менее 50 мкм, 10—

18% зерен — 50—100 мкм. Кривые распределения радиусов округления вершин зерен, построенные с интервалом 50 мкм (рис. 56, а), практически сливаются между собой, что свидетель­ствует о незначительном влиянии формы зерна. При анализе гео­метрии вершин зерен, имеющих радиус округления 5—50 мкм (рис. 56, б), было установлено, что изометричные и неизометричные зерна имеют 31—35% (17—22% общего числа) вершин с ради­усами округления до 10 мкм, а пластинчатые зерна имеют около 40% (23% общего числа) таких вершин.

Таблица 14 Характеристика рельефа абразивных кругов в зависимости от процентного содержания зерен основной фракции Уровень секущей профиля, мкм Содержание основной фракции, % 50—55 60—65 50—55 60—65 п ^СР’ мм 5 0,04 0,03 1,45 2,00 10 0,06 0,05 1,10 1,75 15 0,09 0,06 1,20 1,65 20 0,11 0,07 1,15 1,50 25 0,12 0,10 1,10 1,45 30 0,14 0,11 1,09 1,40 40 0,16 0.14 1,00 1,25 50 0,21 0,16 0,95 1.15

Полученные данные о геометрии рельефа режущей поверхности кругов хорошо согласуются с результатами опытов, выполненных во ВНИИАШе: круг с 75%-ным содержанием основной фракции зерен работает с более высокой стойкостью (до 30—37%), меньшим удельным расходом энергии (около 12%), меньшим значением нор-

 

мальной и тангенциальной составляющей силы резания (около 14 и 19% соответственно) по сравнению с обычными кругами, имеющими 45%-ное содержание основной фракции.

Таким образом, выполненное экспериментальное исследование позволило установить, что регулированием однородности зерново­го состава и введением классификации зерен по форме и на вибро — плоскости можно в определенных пределах изменять некоторые гео­метрические параметры рельефа режущей поверхности шлифоваль­ных кругов и тем самым влиять на режущие свойства кругов.

Регулированием формы абразивных зерен можно изменять разновысотность вершин зерен и тем самым степень заглубления их на режущей поверхности кругов.

Повышение степени однородности зернового состава шлифо­вальных кругов ЭБ40СМ1К5 сопровождается уменьшением контакт­ной площади рельефа поверхности кругов и увеличением среднего расстояния между зернами, что способствует повышению режущих свойств кругов.

С. Г. Редько и А. В. Королев [72] для изучения распределения • абразивных зерен на рабочей поверхности шлифовального круга измеряли расстояние между вершинами зерен (в радиальном нап­равлении круга) с помощью микроскопа. Круг закреплялся в шпинделе плоскошлифовального станка, на столе которого поме­щался микроскоп таким образом, чтобы горизонтальная нить мик­рометра с помощью поперечного перемещения стола устанавлива­лась параллельно образующей круга. Последний поворачивался на шпинделе до тех пор, пока в поле зрения микроскопа не попа­дала отчетливо просматривающаяся вершина какого-либо зерна.

Горизонтальная нить окулярного микрометра совмещалась с этой вершиной, после чего снималось показание. Затем шлифоваль­ный круг медленно поворачивался до появления вершины следую­щего зерна, снова снималось показание и т. д.

Так, на измеряемом участке круга определялось положение вершин всех последовательно расположенных зерен относительно точки ^’отсчета, а затем вычислялось их расстояние до наиболее выступающего зерна, обнаруженного при измерении. Этот способ измерения не имеет недостатков, свойственных существующим способам измерения расположения абразивных зерен. Например, при измерении с помощью стереограмметрических приборов харак­тер расположения зерен значительно искажается вследствие кривиз­ны периферии шлифовального круга. При измерении методом ощу­пывания возникают значительные погрешности в связи с тем, что ощупывающая игла скользит не по вершинам режущей части зерен, а по их боковым сторонам, причем из-за кривизны режущей части зерен вероятность попадания иглы в различные точки вершины зер­на по высоте неодинакова.

Погрешность П измерения данным способом обусловливается глубиной Т резкого изображения зерна, зависящей от свойств при­меняемого оптического устройства, которую можно определить

путем многократного ввода одного и того же зерна в поле зрения микроскопа. /

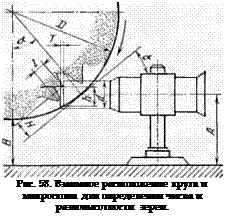
На рис. 58 показано взаимное расположение абразивного круга и микроскопа. Истинное расстояние Н между вершиной выступаю­щего и любого другого зерна Н — h cos а, где h—измеренное рассто­яние; а — угол, под которым рассматривается измеряемая поверх­ность. Погрешность измерения в этом случае П = +Т sin а. Для уменьшения погрешности угол ос нужно выбирать возможно

Рис. 59. Частота 2Z появления вершин абразивных зерен в зависимости от глу-
бины Н их залегания на рабочей поверхности круга 24А40СМ2К после правки
твердосплавным роликом с продольной и поперечными подачами:

Л — 6’hqh = 0,005 мм, Но — 28 мкм, k = 2,5; 2 — £’лоп = 0.015 мм, Н0 — 48 мкм. k = 2; 3 — = 0.04 мм, Н0 = 72 мкм. k — ,Ь: 4 — иранка алмазным карандашом. <S’Iip —

= 0,48, м/мин, 5поп = 0,015 мм, Нп в 48 мкм. k = 1.5.

меньшим, но так, чтобы вершины глубоко залегающих зерен не перекрывались выступающими зернами. Это условие будет соблю­дено, если tg ос >> HmaJl. Здесь Нтах — максимальное расстояние между вершинами зерен в радиальном направлении на измеряемой поверхности круга; I — расстояние между зернами, измеренное по дуге окружности шлифовального круга. Тогда поле зрения d мик­роскопа ДОЛЖНО быть d > Ділах/cos а. Для улучшения видимости вершин зерен нужно иметь направленный боковой источник света, а также покрыть измеряемую поверхность круга черной краской. При измерении с помощью микроскопа МИС-11 с объективом ОС-41 I максимальная погрешность не превышала ±4 мкм.

После каждой правки круга методом врезания производилось шлифование образцов из стали ШХ15 твердостью 61HRC. При глу­бине шлифования 0,02 мм на длине 6 мм производили 50 проходов; охлаждение — 2%-ный содовый раствор. Измерения проводились в четырех положениях круга (по 50 в каждом положении), а затем подсчитывалось среднее количество зерен на данной глубине, ■отсчитанной от наиболее выступающего зерна.

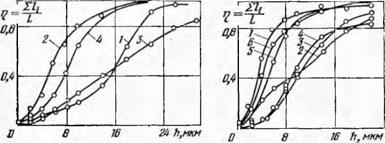
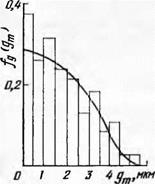
На рис. 59 показана полученная по результатам измерения функ­циональная зависимость распределения зерен на рабочей поверх­ности круга 24А40СМ2К после правки его твердосплавным роликом при Snp = 0,48 м/мин и Sn0n = 0,005 (кривая 1), 0,015 (кривая 2) и 0,04 мм двойного хода (кривая 3), а также после правки его алмаз­ным карандашом Н-8 при Snp = 0,48 м/мин и Snon = 0,015 мм двойного хода (кривая 4).

Как видно из рисунка, распределение зерен нельзя охарак­теризовать разновысотностью Нтах, как это иногда делается, так как при грубой и при более тонкой правке встречаются глубоко расположенные зерна. Наиболее точно распределение зерен можно охарактеризовать глубиной залегания Н0 половины всех измеренных зерен и характером их распределения на этой глубине, который можно записать в виде показательной функции 2Z = аНк Именно эти зерна участвуют непосредственно в резании и формируют обра­батываемую поверхность.

Глубина залегания Н0 половины всех измеренных зерен и пока­затель степени k зависят от режима и метода правки круга. Чем грубее правка, тем меньше k и тем больше Н0, а следовательно, меньшее количество зерен участвует в резании. При правке алмазом значения Нь и k значительно меньше, чем при правке твердосплав­ным роликом на тех же режимах. По-видимому, для чистовых и отделочных операций, особенно при малых глубинах шлифования, необходимо рекомендовать правку круга алмазом, так как в этом случае в зоне резания находится гораздо большее количество зе­рен, чем при правке твердосплавным роликом, и шероховатость шлифованной поверхности получается значительно ниже.

Правка твердосплавным роликом оказывается эффективной при более грубом шлифовании, а также при шлифовании материа­лов, склонных к прижогам, так как в зоне резания находится мень­шее количество зерен. Количество зерен в зоне резания можно эффективно регулировать, применяя различную величину Sn0n правящего инструмента.

Изложенные результаты могут оказаться полезными в практике шлифования при ориентировочном выборе режима и метода правки круга и в теоретических исследованиях; предложенный метод измерения может быть использован для дальнейшего изучения рас­пределения зерен по глубине на рабочей поверхности шлифоваль­ного круга и для изыскания наиболее оптимальных режимов и методов правки.

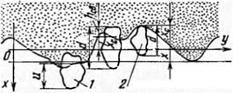
А. В. Королев [41] полагает, что положение произвольного3 зерна размером d, форма которого описывается уравнением (1.10), над уровнем связки равновероятное (рис. 60). Оси прямоугольной системы координат располагаются таким образом; ось Оу — вдоль средней линии профиля неровностей связки, а ось Ох — пер­пендикулярно к рабочей поверхности. Если и — расстояние выс­тупа зерна от уровня связки, то плотность вероятности этой
величины определяется формулой

Рассеивание диаметральных размеров зерен подчиняется за­кону Гаусса. Принимается, что распределение ординат профиля связки хс также соответствует нормальному закону с плотностью вероятности

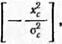
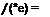
(3.15)

где ас — среднеквадратиче­ское отклонение ординат связки.

Вероятность попадания на уровень х вершины зерна с размером d Р (dx) является произведением трех вероят — Рис. 60. Профиль рабочей поверхности ностей:

*бР“ГО р(<ц =PWP(U)P(*j,

где Р (d) — вероятность того, что среди прочих зерен, выступающих над связкой инструмента, окажется зерно размером d Р (и) — веро­ятность того, что вершина зерна размером d>x при всех прочих условиях окажется именно на уровне х Р (хс) — вероятность тако­го положения зерна на поверхности связки, при котором создается возможность попадания его вершины на уровень х.

Вероятность Р (d) появления над связкой зерна размером d определяется формулой

На уровень х могут попасть только зерна, для которых справед­ливо d — х0 > х (зерна 1 и 2 на рис. 60 этому условию не удовлет­воряют). Так как ординаты профиля связки распределены по за­кону Гаусса, то возможность попадания на уровень выступающей вершины зерна размером d определится вероятностью

Наконец, при равномерной величине выступания зерна над местом закрепления в связке вероятность равна Р (и) = d > х.

Таким образом, вероятность попадания вершины зерна размером d > х на уровень х

Суммируя вероятности попадания на уровень х вершин всех выступающих над связкой зерен, можно найти плотность их рас­пределения f (х) по нормали к поверхности инструмента. При боль­шом числе зерен от суммирования можно перейти к интегрированию:

После преобразований, используя обозначения ——— = t, от-

Функция свободного распределения вершин зерен в направ­лении, нормальном к рабочей поверхности круга, будет

Интегралы в выражениях (3.19) и (3.20) в элементарных функ­циях не выражаются, и их решения возможны для частных значений do; оа и ас.

Для упрощения вычислений математического ожидания х0 и дисперсии о2 А. В. Королевым предлагается следующий метод. Так как положения вершин зерен независимы друг от друга, а математическое ожидание положения вершины зерна размером d при равновероятной величине выступания над местом закрепления в связке равно d/2, то математическое ожидание положения вершин всех выступающих абразивных зерен

.А Ои

(3.21)

dI* exp —

Дисперсия распределения расстояний вершины зерна размером d от места закрепления в связке равна Vi2 d2. Тогда суммарная дисперсия ои этого распределения для всех выступающих зерен най­дется по формуле

В соответствии с (3.18) определим

1

Учитывая неровности связки, запишем

ог = -^-(о2 + 4) + о?. (3.23)

Найдем численные значения х0 и а. Средний размер зерен d0 соответствует номеру зернистости абразива, определяемого ГОСТ 3647—59.

После преобразований окончательно автор работы 1411 получил:

Здесь Nb = ob — среднеквадратическое отклонение распре-

a0

деления средних диаметральных размеров зерен.

А. В. Королев указывает, что величина среднеквадратического отклонения ординат поверхности связки а, в формуле (3.23) не­известна, поэтому в дальнейших расчетах принимается (по данным эксперимента) ос 0,ld0. Подставив это выражение в формулу (3.23), можно найти величину о. Относительные величины сть, аа, аи и о, рассчитанные по данным ГОСТ 3647—59 и формулам (3.20),

(3.21) , (3.23), приведены в табл. 15. Как видно из табл. 15, средне­квадратическое отклонение распределения положения вершин зерен над связкой инструмента слабо зависит от распределения зерен в партии, но в значительной степени определяется их средним разме­ром d0. Это объясняется тем, что превалирующее влияние на распре-

Относительные величины среднеквадратнческих отклонений рассеивания размеров ширины зерен аь/do, их диаметральных размеров od/do, величины выступаний над связкой au/do и распределения положения вершин зерен o/do … £ йамі>о ч ж э* £ Нормальное содержание фракций Повышенное содержание фракций Оптический метод контроля К С. ПЗ Н О о D.° Зернистость 5 & ‘Ч з: с: 200—8 6—3 200—8 6—3 М40=М20 М14=М5 Ob/du 0,17 0,22 0,15 0,15 0,26 0,28 Od/do 0,34 0,36 0,32 0,32 0,39 0,40 o«/d0 0,305 0,306 0,303 0,303 0,31 0,315 о/do 0,321 0,322 0,319 0,319 0,326 0,33

деление вершин зерен оказывает равновероятное распределение ве-1 личин выступания зерен над местом закрепления в связке. ІЕсли бы даже все абразивные зерна, выступающие над связкой инстру­мента, имели бы форму шаров одинакового диаметра do, то и в этом случае разновысотность зерен вследствие разной глубины их за­делки была бы велика, а значение аи в соответствии с формулой

(3.22) составляло бы около 0,29d„, что незначительно отличается от значения аш приведенного в табл. 15, подсчитанного с учетом раз­норазмерное™ зерен.

Таблица 16

Значения плотности вероятности /(X) и функции распределения F(x) выступающих вершин зерен по нормали к рабочей поверхности абразивного инструмента хск/а0 г-т ^ск/^п Их) F{x) —0,225 0,0048 0,996 0,75 0,237 0,241 —0,1 0,00615 0,99 1,0 0,136 0,101 0 0,194 0,95 1,25 0,056 0,031 0,125 0,34 0,846 1,5 0,0156 0,00656 0.25 0,365 0,711 1,75 0,0027 0,00081 0,5 0,32 0,452 2,0 0,00018 0,00003

Таким образом, тщательный контроль содержания фракций в партии зерен после их изготовления, а также анализ вытянутости зерен имеют значение только с точки зрения определения среднего — размера зерен, в то время как плотность распределения зерен над связкой инструмента особого значения не имеет.

Из табл. 15 видно, что для большинства случаев можно при­нимать ad = 0,333d„. При этом соотношении, а также при ас = 0,1 d0 были рассчитаны выражения (3.19) и (3.20), представленные в табл. 16.

Соотношения (3.19), (3.20) позволяют рассчитать число зерен Zx, находящихся на различном уровне над связкой инструмента. Иногда удобнее за начало координат взять не средний уровень связки, а вершины наиболее выступающих зерен. При ас <; 0,ld0 за пределами х = 1,75dQ находится менее 0,1 % общего числа вы­ступающих зерен.

В процессе обработки даже при тонких режимах в резании участвует более 2% зерен. Следовательно, с погрешностью менее 5% можно принять, что наиболее выступающими являются вершины зерен, расположенные на расстоянии l,75d0 от средней линии про­филя связки. При этом если на единице рабочей поверхности аб-

Таблица 17 Значения функции распределения вершин абразивных зерен, подсчитанные по формуле (3.20) и по аппроксимирующим выражениям (3.26) и (3.27) Фор- h/d0 мула 0 0,25 0.5 0.75 1,0 1,25 1.5 1,75 1.972 (3.20) (3.26) (3.27) 0,00 081 0 0,0019 0,0656 0,0053 0,0085 0,031 0,0357 0,031 0,101 0,109 0,083 0,241 0,24 0,225 0,452 0.446 0,446 0,711 0,731 0,716 0,95 U2 0,94 0,996 1,55 1,0

разивного инструмента находится Z0 зерен, то на расстоянии h от вершины наиболее выступающих зерен этой поверхности будет находиться Zh зерен:

Zh — ZqF (h), (3.25)

где F (h) — функция распределения вершин зерен, определяемая равенством (3.20), при значениях аргумента h.

В ряде случаев использовать распределение (3.20) крайне не­удобно. В этих случаях функцию данного распределения можно

Из табл. 17 видно, что формула (3.27) дает лучшее приближение, чем (3.26).

В. Г. Сафронов [77] в работе по исследованию съема металла при алмазном хонинговании стальных закаленных деталей опреде­лял высоту алмазных зерен над уровнем связки с помощью интер­ференционного микроскопа МИП-4. Высоту алмазного зерна на­ходили с точностью до 15 мкм по шкале микрометрического винта фокусировки микроскопа на объект как разность отсчетов, соответ­

ствующих положению, при котором наблюдается четкая интер­ференционная картина на вершинах зерен и на поверхности связки. Исследовались рабочие поверхности брусков зернистостью А6, А10, А25 и А50 со 100%-ной кон­центрацией. Брусками предвари — тельно производилось хонинго­вание посадочного отверстия ше­стерен из стали 18ХГТ, цемен­тированной и закаленной до п, рр твердости 56—63HRC. Размеры ’ отверстия: длина 34 мм, диаметр 34 мм. Размеры брусков: 10 X X 34 X 1 мм, число брусков 4.

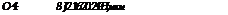
Режим хонингования: окружная скорость и0 = 30 м/мин; скорость возвратно-поступательного дви­жения Пц. п.= 25 м/мин; продолжи­тельность хонингования 60 сек; охлаждение — керосин.

С Как показали измерения, рас­пределение алмазных зерен по высоте над уровнем связки с до­статочной степенью точности можно считать нормальным.

Плотность распределения q может быть найдена по формуле

где Н — высота зерен над связкой; Нср — среднее значение высоты зерен над связкой; о — среднеквадратическое отклонение.

Таблица 18 Значение параметров Нср и о2 для брусков различной зернистости Зернистость алмазов //Ср, мкм О1 Число алмаз­ных зерен, шт./см2 Коэффици — ент с Показатель степени, т А6 5,9 4,69 4650 0,140 0,54 А10 7,9 12,04 2400 — — А25 14,5 37,01 780 0,088 0,55 А50 17,3 40,10 200 0,066 0,60

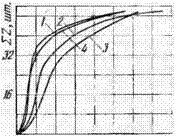
На рис. 61 представлены кривые Гаусса, построенные по данным измерений. Как видно из графиков, чем больше размер зерен, тем больше средняя высота алмазного зерна над уровнем связки. Пара—* метры Нср и о2 для рассматриваемых брусков приведены в табл. 18.

Количество алмазных зерен на единице рабочей поверхности бруска определялось подсчетом с помощью металлографического микроскопа МИМ-7.

Зерна на поверхности бруска распределены неравномерно. Если принять, что в процессе изготовления брусков положение каждого отдельного зерна в бруске случайно, распределение зерен на поверхности бруска должно соответствовать распределению Пуас­сона.

Для того чтобы выявить закономерности съема металла при хонинговании, необходимо изучить закономерность процесса цара­пания металла кристаллами алмаза.

Установлено, что зависимость глубины царапины от усилия вне­дрения выражается политропическим законом

h = cqm, (3.29)

где h — глубина царапины, мм; q — усилие внедрения, Г; т и с — постоянные величины, определяемые экспериментально.

Как показали предварительные эксперименты, данные, полу­ченные при царапании одним кристаллом определенной формы и ориентации, не могут служить основой для описания процесса массового царапания, имеющего место при хонинговании.

Для того чтобы приблизить условия эксперимента к реальному процессу, производилось хонингование отверстий алмазными брус­ками с определенной величиной удельного давления. Отверстия, предварительно отполированные, имели геометрически правильную форму.

Хонинговальная головка совершала лишь один двойной ход, что позволяло избежать перекрещивания рисок при скорости вращения v0 = 5 м/мин и скорости возвратно-поступательного движения ов. п. = 12 м/мин. Рельеф поверхности, полученный при царапании, записывался в направлении образующей отверстия на профилогра­фе «Калибр»-ВЭИ. Установлено, что часть металла, занимавшего объем впадины, выдавливается в стороны, образуя наплывы по краям царапины.

По результатам обработки профилограмм подсчитаны значения сит, которые приведены в табл. 18.

Распределение царапин по глубине усеченное, нормальное, так как в царапании участвуют зерна, выступающие над уровнем связки до определенной высоты. Можно считать, что распределение глубины внедрения алмазных зерен при вдавливании бруска до­статочно точно описывается законом, полученным для распределения зерен по высоте.

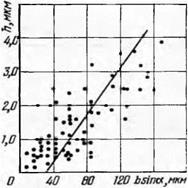
На рис. 62 приведены графики накопленной частоты глубины внедрения и накопленной условной частоты глубины царапин. Зерна алмаза, внедрившиеся в металл на глубину до Нк, при ца­рапании оставят бороздки глубиной до Их <С Нх. Причем количество царапин должно быть равно количеству внедрившихся зерен (без учета попадания нескольких зерен в одну бороздку). Таким образом,
найдя распределение по глубине внедрения и глубине царапины’ для одних и тех же брусков, можно установить зависимость между этими величинами. Указанным способом для всех трех компонентов брусков зернистостью А6, А25 и А50 получена общая зависимость

Н = 0,474Н. (3.30)

Прямая пропорциональность между глубиной внедрения и глубиной царапины сохранялась до Н « 10 мкм.

На основании большого числа обмеров царапин на профило­граммах установлена корреляционная зависимость между шириной

Отсчет со Она Впадины или
вершины зерна, мкм

Рис. 62. Графики накопленной частоты высоты зерна над уровнем связки
и глубины царапин (алмазный брусок А25 100%-ной концентрации):

/ — глубина царапин при р = 12,5 кГ/см2; 2 — высота зерна

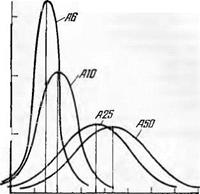
Рис. 63- Зависимость ширины основания царапины Ь от ее глубины для
брусков зернистостью А25 со 100%-ной концентрацией.

и глубиной царапины, обусловленная реальными соотношениями геометрических параметров кристаллов алмазов и закономернос­тями их износа в процессе хонингования.

На рис. 63 представлена точечная диаграмма замеренных зна­чений ширины основания бороздки b для различных величин глубины царапины и линия регрессии b в функции Л, полученная по методу наименьших квадратов:

b = c1 + B1h. (3.31)

Коэффициенты из формулы (3.31) и коэффициент корреляции для брусков различной зернистости приведены в табл. 19.

Значительная часть объема металла царапины выдавливается, образуя навалы по краям каждой борозды. Часть бороздок на про­филограмме не имеет заметных навалов. В этом случае металл уда­ляется резанием. В результате обработки профилограмм царапания поверхности алмазными брусками установлена корреляционная зависимость между глубиной царапины и высотой навалов:

К = с2 + (3.32)

где /гн — высота навалов; с2 и В2 — постоянные коэффициенты.

Предполагалось, что в процессе царапания навалы образуются с двух сторон одинаковой высоты всеми режущими зернами. Значе­ния коэффициентов с2 и Вг и коэффициента корреляции г2 приведены в табл. 19.

Ширина навалов у основания Ь„ меняется в наибольших пределах, и зависимость ее от глубины царапин установить не удалось.

Расчеты показали, что площадь поперечного сечения отдельной царапины, а также площадь сечения навалов достаточно точно и просто находятся как площадь пораболического сегмента. Средняя ошибка при этом для ряда лунок составляла не более 6%.

Таблица 19 Значения эмпирических коэффициентов с,; Всг — В: Зернис­ тость брусков ‘l в, Г С3 в. Г2 Средняя высо­та основания навалов, мкм А6 8,4 1,7 0,484 +0,139 0,234 0,203 6,77 А25 11,5 10,7 0,900 —0,287 0,640 0,153 10,38 А5> 24,0 8,2 0,397 —0,175 0,372 0,710 12,74

Таким образом, средний объем царапины, оставляемой на по­верхности обрабатываемого металла отдельным зерном, определяет­ся как

V, = bhLklt (3.33)

где L — путь, пройденный бруском в процессе хонингования; kx ■— коэффициент, учитывающий уменьшение съема вследствие выдавливания металла.

Глубину царапины h и ширину основания царапины можно определить, если известна средняя нагрузка, действующая на отдельное зерно. При этом же условии может быть найден и коэф­фициент kl (см. формулы (3.29) и (3.31)1:

(3-34)

где VH — средний объем навала, образующийся с каждой стороны царапины.

‘1 Выражение (3.34) может быть записано так:

■ПГ

(3.35)

■ ■ Для того чтобы найти объем металла, срезанного брусками в процессе хонингования, необходимо знать число режущих зерен. Зная удельное давление брусков, можно рассчитать количество рабочих зерен на площади 1 см2, воспринимавших эту нагрузку.

Путем преобразования координат формулы (3.28) с использо­ванием зависимостей (3.29) и (3.30) плотность распределения зерен по величине действующего на них усилия внедрения может быть опре­делена из выражения

«’V-W

V. = — ф-е 201 . (3.36)

У 2ло

где А — постоянный коэффициент, полученный с помощью формул (3.29) и (3.30), А = 0,474 с. Распределение (3.36) получено, таким образом, из нормального распределения (3.28) с помощью преобра­зующей функции Н = qm.

Удельное давление Р, действующее на 1 см2 бруска, найдется суммированием нормальных усилий, действующих на отдельные зерна алмаза:

Q (//^р Aqm)*

P = Z 4- -4^- ‘) е qm~ldq. (3.37)

‘■ У 2 по б

Выражение (3.37) можно упростить, выразив его через интеграл Лапласа и преобразуя распределение (3.37) в нормальное из условий равенства функций распределения для соответствующих значений случайных величин:

является нормированной переменной распределения.

В формуле (3.37) при заданном значении удельного давления неизвестной величиной является предел интегрирования q. Иначе говоря, задача сводится к тому, чтобы найти точку усечения нор­мального распределения. Точное решение этой задачи весьма гро­моздко, так как отсутствуют таблицы, которые могли бы облегчить вычисления. Предел интегрирования q может быть найден методом подстановок с использованием таблиц значений интеграла Лапласа.

Количество рабочих зерен Z0 на 1 см2 поверхности бруска на­ходится по формуле

Фактическое число режущих зерен меньше, чем число внед­рившихся зерен, найденное по формуле (3.38), так как часть зерен попадает в уже готовые бороздки, не оставляя царапин на обрабаты­ваемой поверхности.

Для площади участка бруска размером 1 сма и шириной, равной ширине бруска, вырезанного в направлении траектории движения,

10

среднее расстояние между внедрившимися зернами I = гг~, если lift

считать, что внедрившиеся зерна алмаза имеют размеры, равные средним для данной зернистости.

В каждом квадрате со стороны I расположено одно зерно, при­чем любое положение его равновероятно.

Количество зерен в полосе бруска шириной /, взятой в направ­лении траектории, будет

(3.39)

где а( — угол наклона траектории движения бруска к образующей обрабатываемого отверстия.

Вероятность того, что п-е зерно рассматриваемого участка бруска будет участвовать в резании, следует из формулы

Общее число режущих зерен участка бруска шириной I най­дется суммированием вероятностей работы каждого из Z’ зерен:

ряд представляет собой геометрическую прогрессию

і і ь

с первым членом «! = I и знаменателем, равным 1————- j.

На основании полученных зависимостей легко рассчитать об­щее число царапин Zu, оставленных участком бруска площадью в I см2 и шириной В, выделенного в направлении траектории его движения. С учетом (3.39) и (3.40)

‘ ‘

‘ Таким образом, вероятное число режущих зерен для брусков данной характеристики зависит от ширины бруска В, соотношения скоростей v0 и ов. п. (угол а(), удельного давления брусков, опреде­ляющего значения Ъ и /.

На основании расчетов, выполненных с учетом полученных зависимостей, автор работы 177] делает следующие выводы:

1. Число режущих зерен бруска возрастает по мере увеличения удельного давления брусков, причем резко — для мелкозернистых брусков.

2. Число режущих зерен возрастает по мере увеличения угла at. Для брусков зернистостью А25 и А50 величина Zu незначитель­но возрастает при хонинговании с углом а{ > 20 — г — 30°. При работе брусками зернистостью А6 интенсивное увеличение числа режущих зерен наблюдается при at = 60 ч — 70°. В связи с этим необходим правильный выбор величины at.

3. По мере увеличения ширины бруска возрастает вероят­ность попадания зерен бруска в готовую бороздку, тем самым уменьшается процент режущих зерен, особенно для мелкозернистых брусков. Однако увеличение ширины бруска при постоянной его длине приводит к увеличению числа режущих зерен, поскольку возрастает рабочая площадь брусков.

4. Расчетное количество режущих зерен отличается от факти­ческого, подсчитанного при царапании полированной поверхности не более чем на 15—20%.

			—

О 20 40 БО h, MKM

Далее В. Г. Сафронов, используя полученные зависимости, определяет объем металла, срезаемого алмазными брусками; а также оценивает величину шероховатости обработанной поверхности.

Л. Н. Филимонов, В. Г. Степаненко, Ю. П. Приймак [86] провели исследования разновысотности режущих кромок абразивных кругов с различной характеристикой после правки и шлифования.

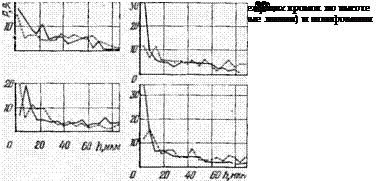
Раз новысот: і ость измерялась профилографированием рабочей поверхности круга прямого профиля вдоль его образующей. Пред­варительно было выяснено, что направление профилографирования вдоль образующей или по окружности не оказывает влияния на статистические характеристики рельефа, т. е. можно считать, что рельеф представляет собой стационарное и эргорическое случай­ное поле. Длина каждой профилограммы соответствовала расстоя­нию 60 мм на круге. За нулевой уровень при определении разновы­сотности режущих кромок принята линия, проходящая по вершинам наиболее выступающих кромок. Радиус ощупывающей алмазной иглы был равен 12 мкм. Всего получено 22 гистограммы распреде­ления. Часть этих гистограмм показана на рис. 64.

Все гистограммы имеют ярко выраженную правостороннюю асимметрию, переходящую во многих случаях в форму, близ­кую к экспоненте. Исключение составляет гистограмма круга 24А25М37К5, полученная после шлифования. По мнению авторов, ее форма сходна с прямой равномерного распределения.

Статистическая проверка законов рас ределения: логарифми­ческого, нормального, Релея, гамма — и бэта-[ определения по крите­риям согласия показала, что бэта-распределение является наи­более подходящим для анализа полученных гистограмм.

Плотность вероятности этого распределения является функцией параметров у и т] и выражается следующим уравнением:

f (*> = хО — ХУ~Щ при 0 < х < 1, ■ (3.42)

где Г (у + ті), Г (у), Г (rj) — табличные гамма-функции; х = = Z/Hn (Z — расстояние от нулевой линии до данной вершины

Таблица 20 Характеристика рельефа рабочих поверхностей шлифовальных кругов Круг h, мкм N, шт/мм Характеристик и бэта-ра сп р е де л е н и я Nt. шт., на уровнях, мкм А V Т1 10 20 30 40 40 СМ1 330 3,2 0,9 0,62 1,70 0,53 0,85 1,10 1,30 300 3,5 0,9 0,66 1,51 0,49 0,78 1,05 1,27 25 СМ1 250 5,7 0,765 0,47 2,38 1,52 2,24 2,60 3,00 225 5,2 2,8 1,06 2,56 0,52 1,05 1,55 2,04 16 СМ1 170 6,5 1,57 0,71 2,78 1,68 2,70 3,46 4,00 145 5,7 2,88 1,01 2,83 0,60 1,20 1,77 2,30 25 СТ1 220 6,7 0,60 0,39 2,51 2,16 3,10 3,50 3,94 210 4,5 1,49 0,72 2,51 0,80 1,32 1,73 2,05 25 С1 230 6,0 0,635 0,44 2,06 1,55 2,25 2,75 3,16 210 5,5 1,07 0,64 2,05 1,03 1,65 2,14 2,54 25 М3 260 4,7 0,54 0,39 1,97 1,45 2,10 2,54 2,85 260 4,3 3,66 1,34 2,25 0,22 0,52 0,85 1,20 Примечание. В числителе круг после правки, в знаменателе — после шлифования.

режущей кромки, мкм; Н„ — полная высота профиля рельефа кру га, мкм).

В табЛ. 20 приведены результаты измерения и статистичес­кие характеристики бэта-распределения для шести шлифовальных кругов.

Для определения количества режущих кромок на определенном уровне t (при заданной глубине шлифования) удобнее пользоваться интегральной функцией распределения

Nt = NA j>-v(l — tf-^dt

о

или, если заменить интеграл суммой,

jM

N, = NA У l’-v (1 — О1-11 А/, (3.43)

х=0 і ‘ * *

где N — полное колич їство режущих кромок, приходящихся на ] мм длины профиля; / = р ^

В табл. 20 приведены рассчитанные по формуле (3.43) значения Nt для различных уровней. Из этих данных хорошо видно влияние зернистости и твердости кругов, а также их износа во время шлифо­вания на количество активных режущих кромок. С уменьшением зернистости и увеличением твердости круга число режущих кромок увеличивается, в то время как износ в процессе шлифования спо­собствует уменьшению числа режущих кромок. Полученный закон распределения режущих кромок по высоте может быть использован для определения текущей толщины срезов аг при шлифовании, но не среднего или максимального ее значения, как это обычно принято рассчитывать по общеизвестным формулам, а функции распреде­ления аг. Если предположить, что форма вершин режущих кромок абразивных зерен — параболоид вращения, то можно, беря за ос­нову одну из известных формул для определения толщины срезов (например, по Г. Б. Лурье) и используя выражение (3.43) для оп­ределения числа режущих кромок, выразить функцию распределе­ния а? следующим статистическим уравнением:

где Qyn = Q/H — удельный съем металла на 1 мм высоты круга, мм3/мм — мин (Q — скорость съема металла, мм8/ іин: И — высота кру­га, мм); VKp—скорость круга, м/сек; рср— средний радиус закругления вершин зерен, мкм; D — диаметр круга, мм; d — диаметр дета­ли, мм.

3. И. Кремень [43], изучая вопросы абразивной дозодКА, считает определяющим для резания-царапания тонких слоев металла значе­ние отношения глубины h внедрения индентора к радиусу округле­ния р вершины индентора.

Граничные условия перехода одного вида деформирования к другому могут быть приближенно сформулированы так: при hip < 0,02 происходит упругое деформирование; при 0,02< h/p < < 0,5 — пластическое деформирование; при hiр >• 0,5 — резание. Исходя из этого сделана попытка вероятностно-статистического анализа механических явлений при доводке, что обусловлено слу­чайным характером процесса. Значения радиусов округления вершин р абразивных зерен являются случайными величинами так же, как и глубина внедрения зерен в металл, которую приближенно можно отождествить с высотой неровностей на доведенной поверх­ности. Следовательно, отношение hip, определяющее тот или иной вид деформирования, тоже является случайной величиной.

Исследование геометрии зерен абразивных микропорошков и шероховатости доведенных поверхностей позволило установить, что распределение случайных величин h и р подчиняется закону
модуля разности

(Х—А)2 (х+А)‘

1 2о2 2о2

Рho (х) = (е + Є ), (3.45)

где Р (х) — плотность распределения; Лио — среднеарифметическое значение и среднеквадратическое отклонение параметров h и р.

3 И. Кремень определяет далее плотность pv распределения случайной величины v = hiр при заданных плотностях ph и рр, характеризующихся соответственно параметрами Л„, oft и Лр, ор.

Учитывая влияние на процесс доводки многих факторов (дав­ления, кинематики и др.) и принимая величины h и р независи­мыми (h > 0, р > 0 и v > 0), плотность можно выразить следую­щим образом:

оо

Pv(x) = J zph (zx) Рр (z) dz,

о

где z — переменная интегрирования. После преобразований и подстановки

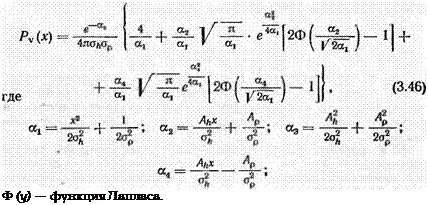Выражение (3.46) описывает закон распределения величины v = hiр и позволяет рассчитать вероятность осуществления упру­гого РупР и пластического Рхлл деформирования микрообъемов металла абразивными зернами, а также вероятность резания Рре3; Эти вероятности по смыслу совпадают с вероятностью попадания величины v соответственно в интервалы 0—0,02; 0,02—0,5; 0,5 —со и могут быть рассчитаны по формуле

*2

Рv {хі ^ <-С. X‘l) — ^ Рх (х) dx.

Автор произвел расчеты указанных вероятностей для процесса плоской доводки стальных закаленных (62—65 HRC) деталей.

Параметры Ар и ор были получены на основании измерений большого числа зерен микропорошков, а параметры Ah и о4
рассчитаны по профилограммам поверхностей, доведенных с по­мощью чугунных притиров и абразивных паст при давлении 0,6 кГ/см2 и скорости 10 м/мин. В абразивную пасту входили: 30% порошка электрокорунда М7, 20 ва­зелинового масла, 30 керосина, 15 стеа­рина, 5% олеиновой кислоты.

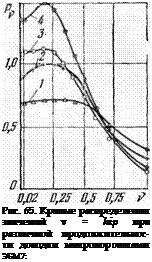Доводочная паста подавалась в зону доводки каждые 30 сек, это позволило сделать допущение, что количество взаи­модействующих с деталью абразивных зерен, их гранулометрический состав и геометрия вершин в течение рассматри­ваемого промежутка времени являлись постоянными.

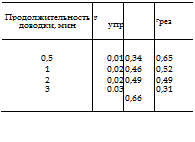
На рис. 65 представлены кривые рас­пределения значений h/p для различно­го времени доводки микропорошками ЭБМ7, а в табл. 21 приведены значения

Яуттр, Рі™, Ррез* Как видно, вероятность

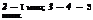упругих деформаций очень мала и пре­обладающими видами деформирования являются пластическая деформация и резание.

В начальный период доводки преоб­ладает резание металла абразивными зер­нами, затем наблюдается постепенный переход к трению с пласти­ческим деформированием микрообъемов металла. При этом суще­ственно падает производительность доводки: от 1 до 0,51 мкм/мин в течение 3 мин доводки.

21

Таблица 22 Значение вероятностей Р Р и Р упр’ пл рез в зависимости от р Микро- порошок Средняя величина о. мкм Рупр ^пл ^реэ ММ7 0,26 0,02 0,55 0,43 ЭБМ7 0,3 0,03 0,66 0,31 ЭТЗМ7 0.43 0.05 0,86 і 0.09

Расчетами установлено, что относительная глубина внедрения зерен в металл h/p находится в основном в интервале 0,1—2, причем для рассмотренного выше случая вероятность нахождения величины h/p в области 0,1—1 составляет 0,59—0,9, а в области 0,1—0,2 она составляет 0,75—0,95. Таким образом, в работе участвуют
лишь участки вершин абразивных зерен, составляющие от V30 до */,0 размера зерна.

Геометрия вершин зерен существенно влияет на характер ме­ханических явлений, а следовательно, на производительность и качество доводки.

На рис. 66 показаны кривые распределения величины й/р при доводке микропорошками одинаковой зернистости, но из различных корундовых материалов, рассчитанные для доводки продолжитель­ностью 3 мин.

Значения вероятностей Рупр, Рпл» Ррез в зависимости от радиуса закруг­ления вершин зерен р приведены в табл. 22.

Рис. 66. Кривые распределения значений v = h/p при доводке раз­личными микропорошками (продолжительность доводки 3 мин): / _ ММ7; 2 — ЭБМ7; 3 — ЭТЗМ7. Рис. 67. Оценка Доли эффективно действующих режущих кромок при плоском шлифовании (/ — базовое сечение).

Производительность доводки для различных материалов различна. Так, для монокорунда она составляет 0,58 мкм/мин, а для электро­корунда титанистого — 0,36 мкм/мин, в то же время шероховатость обработанной поверхности при применении последнего снижается на 2—3 разряда.

М. Мацуи [57] в работе, посвященной изучению механизма ре­зания абразивными зернами, приводит формулы для расчета доли зерен, эффективно участвующих в шлифовании, ширины и глубины резания единичным зерном, длины непрерывного резания (стружки), расстояния между режущими кромками абразивных зерен, площади поперечного сечения стружки, максимальной глубины врезания абразивных зерен.

Таблица 23 Сводная таблица законов распределения режущих кромок зерен шлифовальных кругов по данным различных исследователей Исследователь Закон распределения режущих кромок К мкм Круг Сасаки и Окамура Нормальный 12 WA600 P„60V Ориона Параболический 10 GC60K Пекленик Равномерный (3—24 мкм) 56 EK36J (Н, G) 8 Брюкнер Равномерный 20 EK36J5 EK60J6 EK30J7 Мацуи и Седзи » 2 WA80H„,V Ида и др. Параболический (0—7 мкм) 10 D32050M Накаяма Равномер ный 40 WA46K Сато, Мацуи и Хориути Хонда, Симура и Накад- » Пропорционально глубине 5 WA60KmV зава Л2.7в 7 А601 Ито и Ото Нормальный 12 WA60K9 V Примечание h — приблизительная глубина абразивного слоя» на которой определял­ся закон распределения режущих кромок.

Форма режущих зерен приведена автором работы [57] к форме конуса с углом при вершине, равным 2а = 160°, на основании измере­ния частотного распределения углов при вершине режущих кромок абразивных зерен в шлифовальном круге WA46K, оставляемых зернами на шлифованной поверхности латунного образца при его царапании.

М. Мацуи приводит таблицу измерений частотного распределения режущих кромок абразивных зерен в направлении по радиу­су шлифовального круга по данным различных исследователей (табл. 23).

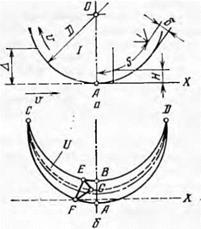
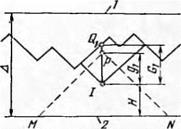
На рис. 67 приведены схемы плоского шлифования (а) и объема криволинейной трехгранной пирамиды (б), образованной огибающей кривой, описываемой точкой режущей кромки абразивного зерна с координатами S, б при постоянной величине базового сечения Н (кривая CBD). Пирамида в сечении, проходящем через точку Е, имеет равнобедренный треугольник EFG и угол при вершине Е, равный 2а. Обе точки F и G располагаются на наружной поверх­ности абразивного круга.

Вероятность Ре (S, 6) того, что режущая кромка с координатами S, б будет эффективно действующей по отношению к базовому сечению, равна вероятности того, что в объеме U криволинейной трехгранной пирамида нет ни одной режущей кромки.

Плоскость базового сечения принята в положении О А, а вели­чина среза Н определяется по формуле

Н = б + (3.47)

где G = Пд/Пок VD (и0к и va — соответственно окружная ско­рость шлифовального круга и скорость вращения обрабатываемой

где W0 — средний объем, занимаемый режущими кромками одного абразивного зерна в PC круга. Объем U в свою очередь определяется как интеграл: $ j б2 tg adS = (Я25 — H&S3 + ~^G*Sb f tg a. — ‘ (3.49) Параметр Pe представляет лишь вероятность того, что режущая кром­ка с координатами S, б эффективно осуществляет резание только в не­котором одном базовом сечении, и оп­ределенное его значение является не­обходимым и достаточным условием для выявления только одной эффек­тивно действующей кромки. Например, на рис. 68 режущая кром­ка А осуществляет резание обрабатываемого изделия, описывая траекторию /, после чего режущая кромка В снимает слой ме­талла, проходя по траектории //. Кромка В является также эффективно действующей, но по отношению к сечению Q, она без­действующая. Если резание все же происходит в каком-либо се­чении (например, в сечении й2), то в дальнейшем оно будет проте­кать эффективно, вплоть до выхода траектории на свободную поверхность обрабатываемого изделия. Следовательно, для некото­рой режущей кромки с координатами S, б, взяв базовое сечение по ее траектории движения в положении выхода на свободную поверх­ность (положение й3), можно исследовать, в какой мере она является эффективно действующей относительно этого сечения. Эта режущая кромка в выбранном сечении срезает слой металла на глубине А, а ее расстояние S по дуге окружности от этого базового сечения мо­жет быть определено по формуле (3.47) согласно выражению

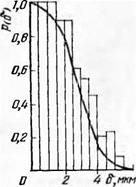
На рис. 69 плавная кривая соответствует результатам раечета по формуле (3.51) с использованием таких числовых данных: пок = = 1300 м/мин, D = 149 мм, пд= 10,3 м/мин, Д = 10 мкм, W0 = — 106 мкм3, tg а = 5,67.

На рисунке видно, что все режущие кромки абразивных зерен, находящиеся на глубине 6 мкм и более от поверхности шлифоваль­ного круга, являются бездействующими. На том же рисунке пока­зана гистограмма, представляющая собой результаты моделирова­ния по методу Монте-Карло. В этом случае значение интеграла

Рис. 69. Зависимость эффективно действующих кромок в общем их
числе от глубины поверхностного слоя шлифовального круга.

Рис. 70. Кривая вероятной плотности распределения расстояний между эффективно действующими режущими кромками С (круг марки WA46K7V, Д=5 мкм; G=0,00034 мм-1^, Ve=0,69 мм; tg а=6,5).

д

-Г — Р(б)йД будет средней долей Р(6) эффективно действующих Л о

кромок.

Среднее расстояние между эффективно режущими кромками We абразивных зерен определяется как квадратный корень из средней плотности W’i поверхности шлифовального круга, взятой в какой-либо одной его точке, при проектировании на развернутую на плоскости цилиндрическую поверхность круга с содержащимися на ней эффективно действующими режущими кромками:

<3-52>

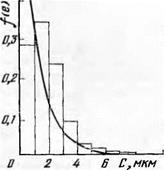
Если установлено среднее расстояние между эффективно дей­ствующими режущими кромками, то аналитически можно опреде­лить распределение этих расстояний по непрерывной режущей кромке и в некотором диапазоне измерений. На рис. 70 плавной кривой показана функциональная зависимость вероятной плотности распределения расстояний между эффективно действующими режу-
«ими кромками в диапазоне измерений 0,4 мм. Здесь же представле­на гистограмма результатов измерений, полученных с применением индикатора нагрузок, снимаемых по изменению электрического напряжения.

Теоретическое обоснование количественного определения глу­бины врезания абразивных зерен произведено М. Мацуи по дан­ным Ориона. На рис. 71 из точки I резания переднего конца режу­щих кромок восстановлен перпендикуляр к наружной поверхности обрабатываемого изделия и по точке Q± пересечения с поверхностью, срезанной предшествующей режущей кромкой, определена глубина

Рис. 71. Схема для определения глубины врезания абразивного зерна:

/ — поверхность обрабатываемого изделия; 2 — идеально обработанная поверх-
ность.

Рис. 72. Функция вероятной плотности распределения глубины врезания
абразивных зерен gt.

врезания Gj абразивного зерна, которая соответствует отрезку IQi в плоскости базового сечения режущей кромки с координатами S, 6. Теперь, как показано на рис. 71, нужно взять произволь­ную точку Р на прямой IQ1 и обозначить отрезок IP = gt, а затем равнобедренный треугольник PMN с углом 2а при вершине в точке Р. Точки М и N лежат на идеально обработанной поверхности. Чтобы глубина врезания G, абразивного зерна удовлетворяла нера­венству Сх >• glt внутри равнобедренного треугольника PM N не должна проходить никакая другая режущая кромка, предшеству­ющая режущей кромке с координатами S, 6. Если все же имеются режущие кромки, проходящие через треугольник PMN в плоскости базового сечения, то, обозначив объем шлифовального круга, в котором находятся режущие кромки, предшествующие кромке с координатами 5, б, через Uly этот объем можно определить по формуле (3.49), заменив в нем параметр Н суммой Н + qv В резуль­тате формула (3.49) примет вид

Таким образом, если при Я, S = const вероятность того, что выдерживается неравенство Gx >• g1( обозначить через Р (Сх >- gx; Я, S = const), то эта величина будет соответствовать вероятности полного отсутствия режущих кромок в объеме Я, и определится из выражения

р (Gi > gj); (Я, S = const) = exp I————— QA. (3.54)

1 dUt І = Ж*1ІГехр(

В таком случае функция /„ (gx) вероятной плотности распределения Gx будет определяться формулой

где Gj должно удовлетворять неравенству 0 < Gx < Д — Я. Следовательно, в случае gx > Д — Я должно быть Gx = Д — Я.

Далее функция /х (gx) вероятной плотности распределения глу­бины врезания абразивных зерен по всему базовому сечению оп­ределится как интеграл по /„ (gx) в формуле (3.55) в областях зна­чений Я и S (б < Я < Д; — Yt):

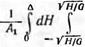
(3.56)

где (3.57)

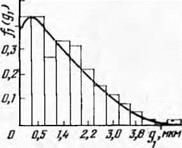
На рис. 72 представлены результаты числовых расчетов по формуле (3.56) для тех же условий, что и на рис. 69. Здесь тоже приведена гистограмма, представляющая собой аналитические данные модели­рования по методу Монте-Карло.

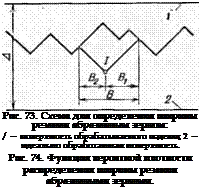
Ширина резания режущей кромкой с координатами S, 6 абра­зивного зерна в плоскости базового сечения обозначена через В (рис. 73), причем особо выделена ширина резания правой частью зерна Вг. Если функцию вероятностей плотности распределения ширины резания Вх правой частью обозначить /2 (йх), то по аналогии с определением глубины врезания абразивных зерен можно получить формулу

Аналогичным образом и функция вероятной плотности распре­деления ширины Bt резания левой половиной абразивного зерна выразится формулой типа (3.58). Следовательно, функция (Ь) вероятной плотности распределения ширины среза В = Вх + Ба (если параметры Вг и Вг определять независимо один от другого),

будет описываться выражением

е>

МЬ) =

«о

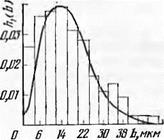
Плавная линия на рис. 74 соответствует результатам расчета по формуле (3.59) для тех же условий, что и на рис. 69. Гистограмма, приведенная на том же рисунке, представляет собой результаты моделирования по методу Монте-Карло.

Площадь поперечного сечения стружки, срезаемой абразивным зерном, определялась М. Мацуи на основании результатов модели-

рования по методу Монте-Карло. Приближенная зависимость между площадью поперечного сечения стружки А0, срезаемой абразивным зерном в плоскости базового сечения, и глубиной врезания G, аб­разивного зерна будет

4, = G? tga. (3.60)

Поэтому функция Кг (а0) вероятной плотности распределения площади поперечных сечений стружки, срезаемой абразивным зер­ном Л0, определится из следующего выражения:

(3’61)

Сплошной линией на рис. 75 показаны результаты численных расчетов по формуле (3.61) для тех же условий, что и на рис. 69. Гистограмма, приведенная на том же рисунке, представляет собой результаты моделирования по методу Монте-Карло.

Максимальная глубина врезания абразивных зерен определена из следующих соображений. Ранее была исследована глубина вреза­ния режущих кромок абразивных зерен в произвольном сечении, перпендикулярном к направлению шлифования. Здесь на основании полученных данных определено частотное распределение максималь­ных глубин врезания абразивных зерен.

На рис. 76, а дугой окружности / показана траектория, опи­сываемая передним концом абразивного зерна относительно обраба­тываемого изделия, а дугой II — траектория движения по образую­щей поверхности предшествующей режущей кромки, лежащей в той же плоскости. При этом максимальная глубина врезания Gm ре­жущей кромки с координатами 5, б определится отрезком ВС. Поскольку в сравнении с величиной диаметра шлифовального круга величина радиального врезания крайне мала, с достаточной точ­

Рис. l75. Функция вероятной плотности распределения площадей поперечного
сечения срезов абразивными зернами а0.

Рис. 76. Схема для определения максимальной глубины врезания абразивных

зерен:

1 — поверхность обрабатываемого изделия; 2 и 3 — базовое сечение Р — 1;4 — идеаль-
но обработанная поверхность.

Точкой I на рис. 76, б показано положение резания в плоскости базового сечения режущей кромкой с координатами S, 6. Из точки I опущен перпендикуляр на поверхность обрабатываемого изделия, и основание его обозначено буквой Р. Поскольку максимальная глубина врезания Gm режущей кромки с координатами S, 6 больше отрезка IP, то внутри равнобедренного треугольника PMN с углом при вершине в точке Р, равным 2а, не должны проходить другие режущие кромки, предшествующие режущей кромке с координатами S, 6. В таком случае, если в объеме круга, соответствующем тре­угольнику PMN в плоскости базового сечения, объем участка, предшествующего режущей кромке с координатами S, б, обозначить через U2, то вероятность Р (Gm >gm; б = const), удовлетворяющая условию б = const и неравенству Gm >gm, будет представлять собой вероятность того, что в объеме U2 не существует режущих кромок. Она определится согласно формуле

Р (°т > ёт> 6 = const) = exp — (3.62)

Данные расчета по условиям рис. 69 приведены на рис. 77, где гистограмма построена по методу Монте-Карло.

Схема определения длины непрерывного резания представлена на рис. 78. Здесь буквой R показано положение начала резания обрабатываемого изделия некоторой режущей кромкой с координа­тами S, 6, буквой Q — положение окончания резания; дуга RQ представляет собой длину непрерывного резания Lc режущей кромкой S, 6.

Если положение базового сечения, в котором происходит ре­зание передним концом режущей кромки с координатами S, 6, обозначить / и lc = IQ, то при VOK vR длина дуги 1С определит­ся по формуле

lc = VD 0/Д^6 + GS). (3.69)

В этом случае базовое сечение может быть выбрано произвольно и независимо от режущей кромки. Так, например, если на рис. 78 взять сечение то относительно этого базового сечения рассмат­риваемая режущая кромка будет эффективно действующей, а если

за базовое сечение взять fi2, то оно не будет срезаться той же кром­кой. Иначе говоря, при Lc 1С режущая кромка с координатами S, б будет эффективно действую­щей относительно базового сечения,

Рис. 77. Функция вероятной плотности распределения максимальной
глубины врезания абразивных зерен gm.

Рис. 78. Схема определения длины непрерывного резания единичным
абразивным зерном:

/ — поверхность обрабатываемого изделия; 2 — поверхность, образованная
предшествующей режущей кромкой.

а при Lc < 1С она будет бездействующей. При 6 = const вероятность Р (Lc >• 1С; б = const), определяемая условием Lc 1С, равна вероятности того, что режущая кромка с координатами S, 6 будет эффективно действующей по отношению к базовому сечению. Эта вероятность численно определяется по следующей формуле (см. определение доли эффективно действующих режущих кромок в об­щем их числе):

из выра­жения

В свою очередь функция f, (1С) вероятной плотности распреде­ления той же длины непрерывного резания абразивными зернами по всему шлифовальному кругу определится интегрированием функции /4 (/с) по формуле (3.71) в области значений б от 0 до Д:

д

Ш= 4-І’/4 (4)^6, (3.72)

3 о

где параметр А3 определится из следующего выражения, если максимальные значения 1е обозначать через 1ст:

^г. т д

Л3 = { dlc]u(lc)db. (3.73)

о о

Данные расчета и гистограмма приведены на рис. 79.

М. Мацуи указывает, что примененный метод аналитического исследования вполне приемлем и при ином характере распределения кромок абразивных зерен, например по треугольнику или параболе, а также в том случае, когда углы при вершине режущих кромок располагаются с определенной закономерностью, р М. Сейки и С. Катсуо [110] для определения распределения зерен по глубине слоя исходили из наиболее выступающих вершин

зерен. Радиальное сечение рабочей поверхности глубиной t пред­ставлено на рис. 80. Для упрощения анализа сечение зерна в рас­сматриваемой плоскости принималось в виде окружности радиу­са г. На рис. 80 проведені прямая 00′ параллельно направлению шлифования. Центры окружностей радиуса г, пересекающиеся с прямой ОО’, расположены на расстоянии х + Ах от этой линии, при­чем г > х + Ах. Расположение режущих кромок на поверхности шлифовального круга следует считать случайным. Обозначив функ-

цию плотности вероятности распределения окружностей по глубине t через f, (г), а плотность распределения центров окружностей (т. е. количество центров на единицу площади) через 1 /Wt, можно опре­делить количество окружностей с координатами центров в интервале х С X «С х + Ах, пересекающихся с линией 00′:

Это уравнение означает, что плотность распределения режущих кромок в радиальном направлении щ (вычисленная по профило­грамме поверхности) пропорциональна глубине t, а средний объем W0, приходящийся на одну режущую кромку, можно считать коэф­фициентом пропорциональности. U

Таким образом, авторы работы [110] получили выводы, ана­логичные нашим: общее количество окружностей (зерен), пересека­емых линией 00′ по глубине слоя t, является параболической функ­цией Nt — f (t2), плотность распределения зерен nt изменяется про­порционально t (п, = const f), что отражает закономерности рас­пределения зерен в абразивном пространстве. А

Свои теоретические выводы авторы проверили эксперименталь­ным путем, фиксируя профилограмму поверхности шлифовального круга на щуповом приборе с тензодатчиком с помощью сапфировой иглы со скоростью 10 мм/мин.

На рис. 81 показано распределение количества режущих кромок по глубине t на поверхности шлифовального круга WA46/C7C, подвергнутого правке монокристальным алмазным инструментом при следующих режимах: продольная подача алмаза 400 мм/мин, глубина съема за проход 0,015 мм, число оборотов круга 2830 об/мин.

Из полученных данных видно, что количество режущих кромок пропорционально глубине профиля в радиальном направлении

Рис. 81. График распределения плотности вершин зерен щ по глубине поверхностного слоя шлифовального круга. Рис. 82. Гистограмма распределения угла рисок на поверхности образца, образуемых шлифовальным кругом WA46K7V.

(только до глубины 9 мкм), т. е. случайное распределение режущих кромок можно считать равномерным. К аналогичному выводу ав­торы работы [110] пришли ранее в результате исследования методом царапания.

Геометрическую форму режущих кромок авторы работы [110] определяли по форме рисок, оставляемых абразивным кругом на зеркально обработанной поверхности металлического образца, ко­торый прикладывали к периферии неподвижно закрепленного круга и перемещали в направлении, перпендикулярном к оси круга. Форму риски определяли на щуповом приборе и рассматривали ее как тре­угольник с углом 2а при вершине. Для шлифовального круга WA46K7V среднее значение угла а = 8Г 19 (рис. 82). Путем под­становки в уравнение (3.76) отношения щ/t = 4,5 из рис. 81, tg а = = 6,5 и I = 417 мм получено значение W0 = 1,2 X 10—3 мм3.

Правильность полученных уравнений была проверена по импуль­сам сил резания, фиксируемых на каждом режущем зерне с помощью малоинерционного динамометра (рис. 83). Чувствительным элемен­том в конструкции является пластина диаметром 20 мм и толщиной 1 мм из пьезокерамики (титанат — цирконат свинца), поляризован­ная в направлении ее толщины. Частота собственных колебаний ди­намометра составляет около 30 кгц, а коэффициент демпфирования колебаний — 0,020. Под воздействием вертикальной нагрузки в пластине генерируется сигнал, который после усиления воспроиз­водится на экране осциллографа.

Если обозначить диаметр шлифовального круга через D, глу­бину резания через Д, то средняя длина царапины будет равна ‘ DД

и среднее время резания единичной режущей кромкой тс составит

. „

%с = —;—, где v — скорость резания, м/мин. При v =

= 1300 м/мин, А = 5 мкм и D — 150 мм тс = 40 X Ю—6 сек. Же­лательно, чтобы частота собственных колебаний динамометра со­ставляла 1/10 продолжительности измеряемого импульса, т. е. была примерно 250 кгц. Однако в связи с тем, что практически изготовить такой динамометр невозможно, М. Сейки и С. Катсуо уменьшили

скорость резания в 100 раз, полагая, что геометрические параметры взаимодействия режущих кромок с обрабатываемой поверхностью при этом не изменятся.

На рис. 84 представлена схема для оценки интервала между последовательными силовыми импульсами с и импульсами от воз­действия активных режущих кромок с обрабатываемой поверхнос­тью а в пределах ширины измерения Ь.

Радиус г рассчитывался из соотношения г = gm tg а, где gm — максимальная глубина резания единичным абразивным зерном. Функцию плотности вероятности распределения этой величины по предыдущим исследованиям авторов можно аппроксимировать треугольным распределением со средним значением величины gm, совпадающим с математическим ожиданием этой величины. Функция /о (gm) удовлетворяет следующему условию:

Если среднее количество активных режущих кромок, пересека­емых линией 00′ (см. рис. 84), обозначить через N, то функцию вероятности распределения расстояния а между двумя последова­тельными активными режущими кромками можно записать в виде

F (а) = 1 — ехр (— Na).

С другой стороны, функцию плотности вероятности распреде­ления радиусов, характеризующих линейные размеры активных

режущих кромок, h (г) можно определить при известном значении /о (ёт) И3 соотношения

h(r) =l^fo{l^r) = 9tga (хг_^tga)’ (378)

Если среднее расстояние между активными режущими кромками обозначить через We, то средняя площадь единичной активной режущей кромки будет W2,. В случае треугольного распределения функции плотности вероятности распределения величины gm максимальное значение этой величины равно 3gm, тогда наибольшее значение г составляет 3gm tg а. Поэтому величину N из уравнения (3.74) можно записать так:

Подставляя это уравнение в уравнение (3.77), получаем выра­жение для функции распределения расстояний между последова­тельно расположенными активными режущими кромками:

F(a) = 1— exp ^——— gm tg aaj. (3.80)

Функцию плотности вероятности f (а) этого распределения можно найти путем дифференцирования полученного уравнения (3.80) по параметру а:

f (а) =~ gm tg a exp | gm tg aaj. (3.81)

Величину gm в этом уравнении можно определить по трех­мерному графику на рис. 85, зная параметры шлифовального круга Ц70 и tg а и режимы резания при шлифовании.

Величина Нт подсчитывалась по эмпирической формуле

Нт — 1,57ГоМ (4^)(-і-)М№а)М. (3.82)

Временной интервал между импульсами составляет

т = c/v. (3.83)

Среднее количество активных режущих кромок на единицу длины в плоскости измерения шириной Ъ обозначалось через Nb. Эту величину можно вычислить, суммируя значения N с количеством окружностей, центры которых расположены в плоскости измерения

Nb = і + N = ф + 2gm tg a)/Wl (3.84)

Функцию плотности вероятности распределения расстояний между активными режущими кромками f (с) получим, подставляя значения 2gm tg a/W2e и с в уравнение (3.80):

Функцию плотности вероятности распределения интервалов менаду силовыми импульсами g (г) можно задать уравнениями (3.83) и (3.85) в виде

Рис. 86. Форма и размеры образца для измерения импульсов от сил резания на
зернах абразивного круга.

менной фиксации нескольких импульсов принималась ограниченной (Ь = 0,2 — г — 0,4 мм). Материал образца — углеродистая сталь S45C. Характеристика абразивного круга ПП диаметром 150 мм была

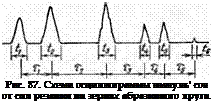WA46K7 V.

Режимы шлифования: скорость шлифования v = 12 м/мин, ско­рость продольной подачи v„ = = 0,05 м/мин, глубина резания А = 2,5 н — 5 мкм. Подачу круга на глубину резания производили после выхаживания поверхности. В результате были получены

осциллограммы силовых импульсов от единичных режущих кромок.
На рис. 87 показана схема осциллограммы таких импульсов, по

которой рассчитывали ширину и длину среза ct и lCj единичным абразивным зерном по получен­ным значениям интервалов меж­ду импульсами т, и продолжи­тельности резания t,:

Сі = хр lH = ttv.

На рис. 88 и 89 приведены гисто­граммы распределений значений с и 1С. На рис. 90 показана гистограмма распределения силовых им­пульсов.

Если обозначить через Р (б) вероятность того, что произвольная режущая кромка, расположенная на глубине б от наиболее выступа-

ющих абразивных зерен, является активной в процессе шлифования, то количество активных режущих кромок на единице поверхности рабочей части круга составит

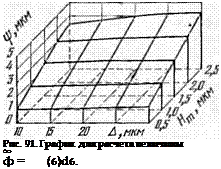Поскольку среднее расстояние между активными режущими кромками We равно корню квадратному из средней площади ра­бочей поверхности шлифовального круга, приходящейся на одну режущую кромку, то

и может быть получено из трехмерного графика рис. 91.

На рис. 88 сплошной ли­нией показаны значения веро­ятности распределения рас­стояний между активными режущими кромками / (с), по­лученные для следующих па­раметров: Д = 5 мкм, Нт ~

= 2,1 мкм, ф == 0,6 мкм, W0 = 1,2 X 10“3 мм3, We = 0,69 мм и gm = 1,3 мкм (по рис. 85). После подстановки значений We, gm и а в уравнение (3.85) при ширине шлифования b = 0,3 мм уравнение в окончательном виде будет fc = 0,66 exp (— 0,66 С).

Функция плотности вероятности распределения расстояний меж­ду двумя последовательными режущими кромками f (а) получается путем подстановки указанных значений параметров в уравнение (3.81):

f (а) = 0,035 ехр (— 0,035а).

Из этого уравнения определим

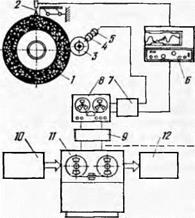Здесь | — переменная, характерзующая окружное рассто­яние между произвольными режущими кромками на рабочей по­верхности круга. На рис. 89 сплошной линией показаны расчетные значения, вычисленные по урав­нению (3.87).

Авторы работы [110] прихо­дят к выводу, что сила резания единичной режущей кромкой про­порциональна площади среза и

Рис. 92. Функция плотности ьероятности распределения максимальной площади среза ат единичными абразивными зернами (Д = 10 мкм, Нт =1,5 мкм, tga =

Рис. 93. Измерительная система, используемая в работе [103]:

1 — шлифовальный круг; 2 — игла; 3 — привод; 4 — коробка скоростей; 5 — шаговый электродвигатель; 6 — профилограф типа Perth — о — Meter; 7 — согласующий блок; 8 — магнитофон; 9 — согласующий блок; 10 — ввод программы; И — ЭВМ типа Sie­mens 305; 12 — результат.

имеет соответствующее ей статистическое распределение. Гисто­граммы распределения силы резания, показанные на рис. 90, ана­логичны функции плотности вероятности распределения максималь­ной площади среза единичным зерном, показанной на рис. 92.

М. Сейки и С. Катсуо считают, что результаты теоретических и экспериментальных исследований практически совпадают.

В. Кениг и В. Лортц в работе [103] по изучению характеристик режущих кромок абразивных зерен в процессе стружкообразования приводят результаты исследования топографии поверхностей шли­фовальных кругов с применением специальной измерительной систе­мы (рис. 93), которая обеспечивала следующее: воспроизводимость результатов; разделение измерительных сигналов, относящихся к малым интервалам по глубине профиля круга; определение и дифференциацию геометрических параметров процесса резания и элементов отдельных абразивных зерен; возможность не­посредственной оценки статистических вероятностей изучаемых

распределений; качественную и количественную идентификацию режущих кромок абразивных зерен, контактирующих с обрабатыва­емой поверхностью; определение динамического расстояния между режущими кромками и максимальной толщины среза.

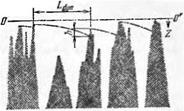В процессе измерений шлифовальный круг, установленный вмес­те с фланцами на валу, приводится во вращение с постоянной ско­ростью. Ощупывающая игла с радиусом округления острия менее 2 мкм контактирует с поверхностью круга, и сигналы, пропорциональные величине перемещения иглы, непре­рывно записываются на магнитной ленте и поступают в ЭВМ для стати­стической обработки.

Сканированию иглой подвергает­ся V5 длины периметра круга, что обес­печивает поступление 80 000 соответ­ствующих цифровых значений для ста­тистической обработки на ЭВМ.

Для оценки участия отдельных абразивных зерен в процессе реза­ния авторы работы [103] предлагают введенный ими критерий, учитывающий геометрические и кинематические условия резания. Значения этого критерия приведены на рис. 94, на котором показана

зависимость толщины среза при шлифовании от расстояния между активными режущими кромками (0 — 0’— нулевой уровень, Ldyn — динамическое расстояние между режущими кромками; h — тол­щина среза; Z — глубина профиля круга).

Учитывая физико-механические характеристики шлифовального круга, его перемещение относительно изделия и режимы резания, В. Кениг и В. Лортц отмечают, что лишь часть абразивных зерен, находящихся на рабочей поверхности круга, контактирует с

обрабатываемой поверхностью. Количество активных, или «динамиче­ских», режущих кромок обозначается в дальнейшем C’dyn. Осталь­ные режущие кромки расположены вне зоны контакта шлифоваль­ного круга с изделием.

На рис. 95 показано изменение количества динамических и статических режущих кромок шлифовальных кругов различных характеристик в зависимости от глубины профиля круга. С возраста­нием глубины профиля во всех случаях увеличивается количество статических режущих кромок, однако степень их роста различна. Следует отметить, что количество статических режущих кромок на поверхности шлифовального круга зернистостью 60 (меш США) в

2,4 раза меньше, чем на поверхности круга зернистостью 100, но практически такое же, как у круга зернистостью 46.

Рост количества динамических режущих кромок имеет предел (см. рис. 95), зависящий от характеристики шлифовального круга, а также от кинематических и геометрических параметров процесса резания. Этот предел достигается на глубине профиля круга пример­но 15—25 мкм. Ниже показано, что количество динамических режу­щих кромок составляет 5—12% общего количества статических режущих кромок.

На рис. 96 приведена усредненная геометрическая форма ре­жущих кромок абразивного круга AA46M6V, полученная в резуль­тате статистической обработки данных измерений с доверительной вероятностью 97,5%. Отмечается влияние условий правки круга на геометрическую форму режущих кромок, в частности на верхней линии четко видны перегибы при глубине правки 15 мкм. На рис. 97 показана усредненная геометрическая форма абразивных зе­рен для шлифовального круга AA60M6V, полученная после прав­ки алмазом с продольной подачей 0,25 мм/об; глубиной правки в три прохода З X 0,02 мм (трасса измерения профиля круга 300 мм).

Как видно из приведенных данных, профиль каждого абразив­ного зерна характеризуется наличием нескольких режущих кромок,

которые при определенных условиях резания контактируют с обра­батываемой поверхностью.

Для аналитического описания процесса шлифования авторы работы ПОЗ] из многочисленных критериев предлагают использовать максимальную толщину среза, позволяющую оценивать взаимосвязь режущих кромок и режимов обработки с получаемыми при шлифо­вании результатами.

На рис. 98 приведены измеренные значения толщины среза в зависимости от расстояния между режущими кромками для шлифо-

Рис. 98. Корреляция между количеством активных режущих кромок и толщиной среза (1 — средний диаметр абразивного зерна).

вальных кругов AA100M6V (слева) и AA46M6V (справа), получен­ные при следующих условиях обработки: скорость вращения изде­лия 60 м/мин; скорость резания 60 м/сек; глубина резания 0,1 мм, диаметр шлифовального круга 500 мм.

Приведенное распределение пар значений h и Ldyn является логарифмически нормальным, причем на плотность вероятности этого распределения в значительной степени влияют выбранные режимы резания и правки круга. В рассматриваемом диапазоне условий обработки около 40% динамических режущих кромок харак­теризуется относительно малым расстоянием друг от друга. Если учесть величину среднего диаметра абразивных зерен, то это озна­чает, что на одном абразивном зерне может быть несколько динами­ческих режущих кромок, контактирующих с обрабатываемой по­верхностью.

Необходимо также отметить, что максимальная толщина среза для двух рассмотренных характеристик шлифовальных кругов не превышает 8 мкм. Логарифмически нормальное распределение тол­щины среза имеет поле рассеивания 0,05—8 мкм.

Процесс стружкообразования при шлифовании В. Кениг и В. Лортц поясняют рис. 99. Модель абразивного зерна представ­ляет собой крайнее звено подвесной системы, вращающейся вокруг фиксированного центра. Жесткость рассматриваемой системы

зависит от конструкции шпиндельного узла и деформации изделия в процессе обработки под воздействием сил резания.

На базе этой упрощенной модели и измерения профиля попе­речного сечения отдельных рисок на обработанной поверхности процесс стружкообразования при шлифовании может быть разделен на следующие три стадии: упругую деформацию системы, пластиче­скую деформацию системы и образование стружки. Степень пласти­ческой деформации при стружкообразовании зависит от физико­механических свойств обрабатываемого материала и условий тре­ния в контакте круг — изделие.

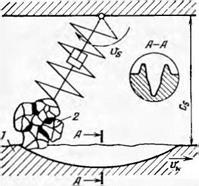На рис. 100 показана статистическая зависимость начальной глубины стружкообразования Тц от скорости резания v, с ука­занием 90%-ных доверительных интервалов (1 — 1). Эта зависи­мость получена при шлифова­нии без охлаждения образцов из стали CK45N шлифовальным кру­гом AA60J6V диаметром 250 мм.

Среднее значение начальной глубины стружкообразования уменьшается с увеличением скорости резания, и, следовательно, процесс стружкообразования начинается раньше. В случае шлифо­вания с применением СОЖ указанная зависимость изменяется.

На рис. 101 показаны распределения максимальной толщины среза, расстояний между динамическими режущими кромками и их количества, полученные при следующих условиях обработки шли­фовальным кругом AA60J6V: скорость вращения детали 60 м/мин, скорость шлифования 30 м/сек, глубина шлифования 0,1 мм, диа­метр круга 500 мм.

Фактическое количество режущих кромок, участвующих в процессе стружкообразования, значительно меньше измеренного, поскольку одна часть режущих кромок осуществляет пластическое оттеснение обрабатываемого материала, а другая часть совсем не участвует в резании, так как расстояние между последовательно

расположенными режущими кромками может быть меньше их сред­него диаметра. Кроме того, следует учитывать частичное налипание обрабатываемого металла на поверхность зерен.

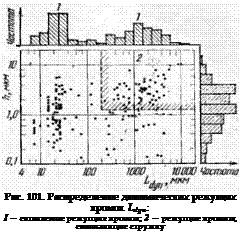Варьируя режимы реза­ния и условия правки кру­га, можно изменить коли­чество режущих кромок, участвующих в резании.

Заштрихованная область на рис. 101 характеризует подобные активные режу­щие кромки, осуществляю­щие стружкообразование при обработке закаленной стали CK45/V.

В работе 1104] В. Кениг и В. Лортц вновь возвра­щаются к вопросам влия­ния топографии поверхнос­ти шлифовального круга на результаты шлифова­ния, связывая их с влияни­ем инструмента для прав­ки и условий правки на рельеф круга.

На рис. 102 приведены результаты опытов по прав­ке шлифовального круга из электрокорунда зернис­тостью 60 меш, твердостью G на керамической связке тремя видами алмазных пра­вящих инструментов: брус­ком FA120W, однолезвий­ным инструментом Basram МК1 и инструментом с не­сколькими профилирован­ными алмазными зернами 60/5 МК1. Подача при прав­ке равнялась 0,5 мм/об. Об­щая толщина материала, снимаемого с круга за три прохода, составляла З X X 20 = 60 мкм. Результаты правки оценивались по статистическо­му числу абразивных зерен C’tlI в поверхностном слое шлифоваль­ного круга.

Как видно на рис. 102, правка инструментом с несколькими алмазами (60/5 МК1) обеспечивает наибольшее статистическое

«число абразивных зерен на единицу поверхности круга, что объяс­няется наличием на алмазах профильной объемной поверхности, •способствующей интенсивному скалыванию абразивных зерен с. результирующим образованием новых режущих кромок. Правка .алмазным бруском и однолезвийным инструментом приводит к практически близким результатам. Оба этих инструмента оставляют на поверхности шлифовального круга одну или несколько четко вы­раженных спиральных линий, и при этом на поверхности круга чис­ло зерен значительно меньше, чем при правке инструментом с не­сколькими алмазами.

Существенное значение при этом имеет вопрос, на какой глубине от рабочей поверхности круга сохраняется влияние правящих ин­струментов на топографию круга, что непосредственно определяется конструкцией правящих инструментов.

В инструменте с несколькими профилированными алмазами последние расположены неравномерно, тогда как в алмазном бруске алмазы расположены строго вдоль определенных линий (поскольку брусок выполнен в виде так называемого алмазного напильника). Ориентированное положение алмазов в бруске приводит к тому, что каждое последующее алмазное зерно проходит по тому же месту поверхности шлифовального круга, что и предшествующее, и по­этому правка таким инструментом должна оказывать на структуру поверхности круга большее влияние, чем правка двумя другими инструментами.

При этом необходимо исследовать соотношение числа абра­зивных зерен на поверхности правленного круга и числа режущих кромок на рабочей поверхности, возникающих при раскалывании абразивного зерна при столкновении с алмазным зерном.

Предельная глубина слоя шлифовального круга, при которой наступает резкое изменение соотношения числа абразивных зерен и числа режущих кромок, характеризует глубину режущего слоя, на которой еще проявляется влияние правящего инструмента. Эта зависимость для условий правки представлена на рис. 103.

Анализ кривых показывает, что алмазный брусок, представ­ляющий собой многолезвийный правящий инструмент, наибольшее влияние оказывает на структуру ПС шлифовального круга, причем глубина слоя, на которую простирается влияние этого инструмента, составляет около 30 мкм. При отношении числа зерен к числу режу­щих кромок, близком к 0,3 (для алмазного бруска), это означает, что на 1 зерно приходится в среднем 3 режущие кромки, что соответ­ствует данным статистического анализа.

Правка инструментом с несколькими единичными алмазами оказывает влияние на структуру ПС глубиной до 10 мкм. Для этой глубины при постоянном соотношении числа абразивных зерен и режущих кромок согласно статистическому анализу приходится на 1 зерно 4 режущие кромки. При правке инструментом с еди­ничным алмазом структура ПС изменяется до глубины около 15 мкм.

Для определения влияния условий правки на топографию ра­бочей поверхности шлифовального круга были проведены опыты по правке двух кругов высотой 100 мм из электрокорунда зернистостью 60 на керамической связке, твердостью G и N. Правка круга твер­достью G производилась однолезвийным алмазным инструментом Basram МК1, правка круга твердостью N — алмазным бруском FA120W. Оба круга правили в 3 прохода с общей глубиной З X X 20 = 60 мкм и подачей от 0,25 до 1,5 мм/об. Поверхность зап­равленных шлифовальных кругов исследовалась щуповым методом.

Результаты опытов представлены на рис. 104, где показаны кривые изменений статистического числа режущих кромок в зави­симости от глубины режущего слоя Z для кругов твердостью G (104,а) и N (104, б).

Анализ кривых показывает, что число режущих кромок при прочих равных условиях выше при меньших подачах. Это объясня­ется тем, что средний диаметр абразивных зерен в круге зернис­тостью 60 составляет около 275 мкм и при высокой подаче (1,5 мм/об) алмаз приводится в контакт лишь с небольшим числом абразивных зерен. Такое же влияние подачи обнаруживается и при правке алмазным бруском более твердого шлифовального круга.

Выше (см. рис. 102) было показано, что правка кругов с одина­ковыми характеристиками однолезвийным алмазным инструментом обеспечивает на рабочей поверхности круга большее число режущих кромок по сравнению с правкой алмазным бруском. Большее число режущих кромок при правке алмазным бруском при низких подачах 0,25 и 0,5 мм/об (рис. 104, б) объясняется большей твердостью

шлифовального круга, способствующей более интенсивному раска­лыванию абразивных зерен При столкновении с алмазами правящего инструмента. С увеличением подачи количество режущих кромок на поверхности круга значительно уменьшается, і В Кениг и В. Лортн исследовали также влияние подачи при правке на шероховатость шлифованной поверхности Ra и на нор­мальную силу резания Fn при шлифовании деталей из стали Ск45 диаметром 138 мм электрокорундовым кругом диаметром 500 мм зернистостью 60, твердостью N, на керамической связке с окружной скоростью 60 м/сек, при круговой подаче 60 м/мин с применением СОЖ. Правка производилась абразивным бруском FAI20W с глубиной резания 20 мкм в 3 прохода.

Установлено, что с увеличением подачи правки шероховатость поверхности возрастает, что является следствием переноса на де­таль значительных микронеровностей поверхности шлифовального круга, возникающих при правке с высокими значениями продоль­ной подачи. В то же время при данных условиях правки и шлифова­ния авторам не удалось выявить определенной зависимости силы F„ от подачи правки.

— Как было установлено выше, при правке однолезвийным алмаз­ным инструментом в ПС круга толщиной Z создается примерно вдвое больше режущих кромок, чем при правке алмазным бруском, а при увеличении подачи число режущих кромок уменьшается. В связи с этим В. Кениг и В. Лортц рекомендуют правку алмазным инструмен­том производить с подачей, в 2—3 раза превышающей подачу при правке алмазным бруском. При равных результатах шлифования это обеспечивает сокращение на 50—60% вспомогательного времени на правку и способствует — повышению экономичности шлифования. В. Кениг и В. Лортц констатируют, что изучение топографии шлифо­вального круга и шероховатости шлифовальной поверхности пока­зали, что качество шлифованных поверхностей тем выше, чем тонь­ше правка круга. Однако чрезмерная тонкая правка круга не всегда целесообразна, поскольку при низких подачах резко снижается раскалываемОсть зерен и происходит сплющивание зерен с резуль­тирующим малым количеством режущих кромок и малым простран­ством для струУкки. Полный анализ наблюдаемых явлений может быть произведен лишь с учетом происходящих процессов стружко- образования. ■

Iі В работе В Кенига и В. Лортца (1051 вновь была дана оценка режущей поверхности абразивного круга в зависимости от его топо­графии, для чего было определено распределение абразивных зерен в зависимости от реальной глубины проникновения в поверх­ность круга на основании данных, полученных при измерении числа Статических зерен по окружности круга и в поперечном направле­нии. Указанная зависимость была построена для шлифовального круга’ зернистостью 54, твердостью К, структурой № 8, на кера­мической связке. Перед измерением круг был заправлен много­лезвийным алмазным! инструментом при режиме: глубина резания

 

а* 7).-i щ rwz е

где C’dT и Ctr — функции распределения плотности зерен соответ­ственно по окружности и в поперечном направлении. Эти значения могут быть аппроксимированы в виде Г-распределения, определя­емого следующим образом:
(Z> 0);
/а, К (Z) =	(3.91)
0 (Z< 0).
где

 

,3 94)

Приведенные выражения на основании произведенных измере­ний позволяют рассчитать соответствующие функции плотности распределения.

Далее В. Кениг и В. Лортц указывают, что из общего количества статических зерен только небольшая часть, зависящая от кинема — тичегких и геометрических характеристик процесса шлифования, активно взаимодействует с поверхностью шлифования. Число таких динамических (активных) зерен можно определить по аналогии с определением числа статических зерен. Основная трудность состоит в распознавании таких зерен. Критерий для резания между стати­ческими и динамическими абразивными зернами можно вывести, исходя из геометрических и кинематических условий шлифования, с помощью измерительного устройства, используя соответствующую систему оценки. Наряду с этим можно определить толщину снимае­мой стружки и расстояние между динамическими абразивными зер­нами.

Авторы работы 11051 приводят график (рис. 106) зависимости изменения числа динамических зерен по глубине слоя при двух скоростях резания для круга диаметром 480 мм из электрокорунда зернистостью 54, твердостью К, структуры № 8, на керамической связке. Шлифование производилось при скоростях 15 и 45 м/сек, остальные условия были постоянными: круговая подача 12 м/мин, глубина резания 0,075 мм Правка производилась многолезвийным инструментом из алмазов г подачей 0,2 мм/об, глубина резания 0,02 мм в 3 прохода. Измерение числа зерен производилось в обоих случаях в окружном направлении.

Из графиков устанавливается, что после достижения некоторой глубины, равной 15 и 12,5 мкм, число динамических зерен не воз­растает и остается в дальнейшем постоянным.

Если считать, что все измерения количества алмазных зерен, представленные на графиках, носят случайный характер, можно

Рис. 106. Зависимость числа динамических абразивных зерен Cdyn от радиальной глубины проникновения в круг: а — :i>s = 15 м/сек; 6 — — 45 м/сек; / — суммарное число динамических зерен; 2 — плотность динамических зерен; 3 — Г — распределение.

найти измеренное распределение плотности абразивных зерен, характеризуемое средним значением и дисперсией, а путем аппрок­симации измеренного распределения плотности определить распре­деление абразивных зерен математическим способом.

Необходимые данные для определения распределения приводятся в табл 24 при измерении числа статических зерен в поперечном на­правлении.

Среднее значение х определяется по формуле

х = а + 2j, n, = 12,5 + ~888′ = *7.06 мкм.

Таблица 24 Функциональное выражение величин, измеренных в поперечном направлении Іі nj іі пі І1 ni it 93 —2 — 186 75 2 150 157 —1 -157 84 3 252 215 0 0 78 4 312 123 1 123 63 5 315 П р Н*м е ч а н и е. Ширина интервала 5 мкм; п.- — число случаев в интервале /; // — скор, ^вотированный номер интервала; 0 — интервал с наибольшим количеством кромок. "Л

Дисперсия определяется по формуле

Таблица 25 Определение Г-распределения / р, 6 (Z) = , = -£-= 0.134 = 2.289 z ffi. Ctat 5 7,96 0,51171 0,03526 329,0 10 19,45 0,26185 0,04414 411,9 15 32,80 0,13399 0,03808 355,3 20 47,53 0,06856 0,02825 263,6 25 63,37 0,03508 0,01927 179,8 30 80,16 0,01795 0,01247 116,3 35 97,79 0,00919 0,00779 72,6 40 116,16 0,00470 0,00473 44,1 Данные для расчета Г-распределения приведены в табл. 25. Г-распределение Г (б) будет

Г (б) = (6 — 1) Г (б — 1) = 1,289 • 0,899 = 1,158.

Аналогичные расчеты могут быть выполнены для определения числа статических и динамических зерен, а также их плотности по измерениям, выполненным в направлении окружности шлифо­вального круга.

Исходя из функции Г-распределения абразивных зерен в дву­мерном пространстве (3.93) и приведенных зависимостей можно оп­ределить функцию Г-распределения абразивных зерен в трехмер­ном пространстве:

(3.95)

Функции плотности распределения абразивных зерен по окруж­ности и в поперечном направлении соответственно имеют вид

F <Z> = ЩТ® j Же-^

Результаты интегрирования, выражающие число абразивных зерен в пространстве в зависимости от глубины проникновения в круг, были представлены в виде кривых для тех же условий правки и шлифования, которые были указаны применительно к рис. 106. Анализ этих кривых показывает, что в диапазоне Z = 0 — г — 8 мкм число статических абразивных зерен крайне мало и не превышает 2 зерен на 1 мм2 При Z = 8 ч — 20 мкм наблюдается резкое увеличение зерен, которое при Z = 20 мкм достигает уже 25 шт./мм2, а при Z = 30 мкм оно равно 45. Число динамических зерен уже при Z = 10 ч — 20 мкм становится постоянным и состав­ляет 2,2 зерна на 1 мм2 при скорости шлифования 15 м/сек и 0,7 зерна на 1 мм’2 при скорости 45 м/сек. Эти данные, по мнению В. Кенига и В. Лортца, хорошо согласуются с данными других исследователей для кругов аналогичных характеристик при тех же условиях правки.

Р. М. Бауль, Д. Грэхэм, В. Скотт [99] исследовали топографию рабочей поверхности шлифовальных кругов на основе теории анали­за случайных процессов.

Предшествующие исследования, ставившие целью количествен­ную оценку состояния поверхности абразивных кругов, во многих случаях базировались на методе снятия отпечатков, которые ана­лизировались так же, как анализируются поверхности шлифо­ванных деталей.

Двухразмерный профиль измеряется щуповым прибором, кото­рый позволяет легко определить такие характеристики поверхности, как положение средней линии профиля Ra, соотношение глубины впадин и высоты выступов Rt и т. д. Эти параметры позволяли судить о распределении высоты неровностей микропрофиля.

Технология снятия отпечатков весьма трудоемкая и поэтому ограничивает количество возможных измерений. В связи с этим Сато и др. была предложена методика непосредственного оптическо­го измерения поверхности шлифовального круга.

Для описания распределения неровностей поверхности были использованы такие более общие статистические параметры, как функция плотности вероятностей (ФПВ), позволяющая получить отчетливую картину высот ординат, и интеграл этой функции интегрального распределения (ФИР), который является важным па­раметром характеристики шероховатости поверхности и в настоя­щее время широко известен как кривая опорной поверхности.

Хотя указанные выше параметры позволяют судить о высоте микронеровностей, они не указывают частоту появлений, а также форму отдельных неровностей. Все поверхности характеризуются периодическим и непериодическим характером неровностей, встре­чающихся в различных пропорциях. При этом Пекленик, используя

методику анализа процессов, имеющих случайный характер, уста­новил различие между несущим профилем и наложенными на него отклонениями случайного характера, обусловливающими действи­тельную шероховатость поверхности.

Сущность используемой авторами теории анализа случайных процессов заключается в следующем. Автокорреляционная функция Rxx (Р) характеризует подобие между сигналом и этим же сигналом при запаздывании.

Пусть профиль поверхности образован переменными (ас) и постоянными (dc) компонентами, т. е. у (х) = ас — dc. Тогда авто­корреляционная функция Ryy определяется выражением

L/2

Rw (Р) = ~г— 1 y(x)y(x + $)dx, (3.99)

—L/2

где у — высота по ординате; х — координата, соответствующая положению вдоль профиля; р — интервал корреляции (в рассматри­ваемом случае интервал между участками испытаний).

Средняя квадратичная величина сигнала определяется выра­жением

фх2 = ас2 + dc2 = Rm (0). (3.100)

Величина ас определяет среднеквадратичное отклонение а, тогда как уровень dc позволяет оценить среднюю высоту неровнос­тей р.

В опытах использовался коррелятор Hewlett — Packard 3721 А, который настраивался только на измерение величины ас. Таким образом, уровень dc не измерялся, а это означает, что корреляцион­ная функция в данном случае не определяла средней высоты неров­ностей. Хотя результирующая функция, не содержащая постоянной компоненты dc, должна быть отнесена к автоковариантной функции, в данном контексте, как пишут авторы, она будет приниматься в качестве автокорреляционной функции (АФ).

Дальнейшие измерения могут быть выполнены исходя из харак­теристики АФ, которая указывает на изменение свойств профиля вдоль поверхности. Одно из таких простейших измерений относит­ся к расстоянию, на котором две точки поверхности могут рассма­триваться как независимые события. В качестве этого расстояния в одном из предшествующих исследований была принята р, при ко­торой Ryy снижается до величины, равной 10% Ryy (0).

Периодические составляющие сигнала выражаются периодиче­скими составляющими характеристики АКФ, период которой легко определяется.

Функция поперечной корреляции (ФПК) Ryz (Р) измеряет по­добие между сигналами как функцию запаздывания р между этими сигналами:

где один из сигналов у (лг) запаздывает на величину р по отношению к другому сигналу г (х).

Информация, получаемая при корреляционных измерениях, может быть выражена в частотной области путем разложения АФ в ряд Фурье. Получаемый при этом так называемый спектр мощнос­ти Su (to) определяется выражением

СО

где со = 2л f в циклах на единицу длины.

Таким образом, распределение мощности в сигнале может быть легко определено при рассмотрении мощности или параметра, характеризуемого в качестве плотности спектра мощности, что является более ценным параметром, чем АФ.

Применение анализа случайных процессов к абразивным по­верхностям затруднялось необходимостью сложного дорогостояще­го оборудования, а также необходимостью переработки громадной числовой информации. Авторам работы 1991 удалось преодолеть эти недостатки.

Как было указано выше, поверхность шлифовального круга определяется как характеристикой самого круга, так и накладыва­емыми условиями правки. Профиль поверхности круга, подвергну­того правке в разных условиях, проанализирован путем разложения этой поверхности с помощью датчиков. Для этой цели были исполь­зованы два датчика контактного и бесконтактного типа. Измерения поверхности круга во время обработки оказались возможными лишь при использовании датчиков бесконтактного типа.

Сигнал от таких датчиков преобразовывался в напряжение, соответствующее топографии абразивной поверхности. Все опыты производились на прецизионном круглошлифовальном станке «Джон Шипман» модели 1310. Устройства, примененные в станке, позволили вращать шлифовальный круг с окружной скоростью 0,43 мм/сек и осуществлять продольную подачу с постоянной ско­ростью 0,43 мм/сек.

Устройство для продольной подачи позволило избежать скачко­образной подачи, возникающей при очень низких скоростях стола, перемещаемого гидравлическим приводом.

Из-за пористости круга (до 40%) оказалось невозможным при измерениях получать непрерывный профиль с помощью датчика модели Vibrometer TS71230, имеющего чувствительный индуктив­ный элемент, несущий алмазный конический щуп с углом конуса 80° и радиусом закругления при вершине 0,15 мм. При развертке профиля щуповым методом записывались лишь импульсы от вершин зерен, в промежутках между ними записывалась «нулевая» линия, что учитывалось авторами работы [991 при дальнейшем анализе.

Перемещение датчика производилось на длине ±0,6 мм при линейности перемещения в пределах ±1%. При этом датчик

использовался совместно с прецизионным частотным усилителем Vibrometer типа 8-CFA-1, выполненным полностью на полупровод­никах. Этот датчик оказалось возможным применять лишь при низ­коскоростной развертке профиля поверхности ввиду низкой чув­ствительности датчика по частоте.

Для непрерывного измерения поверхности абразивного круга в процессе шлифования был применен бесконтактный датчик, в ко­тором использовался пучок из 150 оптических волокон диаметром

0, 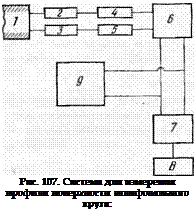0635 мм, хаотично распределен­ных в стальной трубчатой направ­ляющей диаметром 0,685 мм.

В этом датчике половина воло­кон передает свет от лампы нака­ливания к измеряемой поверхнос­ти, а вторая половина волокон вос­принимает отраженный свет и пе­редает его на фотоэлемент, который вырабатывает выходной электриче­ский сигнал, зависящий от интен­сивности света, падающего на него.

Интенсивность отраженного све­та зависит от отражающей поверх­ности круга и от величины зазора между этой поверхностью и датчи­ком. Отражательная способность поверхности круга, по утверждению авторов, является функцией шеро­ховатости этой поверхности. При максимальном выходном сигнале датчик практически нечувствителен к величине зазора между поверхностью круга и датчиком и поэто­му на выходной сигнал большее влияние оказывают наклоны, а не величина неровностей поверхности.

Система для измерения профиля абразивной поверхности обо­ими датчиками показана на рис. 107. Выходной сигнал с датчика подается на усилители 4 и 5 и с них выдается или на самописец 6 для записи на ленту, или на коррелятор Hewlett-Packard 3721А. Последний связан с прибором для построения кривых в координатах х — у.

Для облегчения расположения щупа относительно измеряемой поверхности шлифовального круга сигнал предварительно подавал­ся на осциллоскоп для визуального наблюдения.

Примененный коррелятор позволяет вычислить ФПВ, ФИР, АФ, а также ФПК — В приведенном исследовании последняя не вычисля­лась.

Вычисленные функции демонстрировались с помощью встроен­ной катодно-лучевой трубки с использованием 100 точек. При этом можно было наблюдать статистические характеристики поверхнос-

ти, что является одним из важнейших преимуществ использованной измерительной системы, поскольку позволяет значительно сокра­тить длительность испытаний и оперативно изменять постоянные времени для получения необходимой информации в наиболее до­ступной форме.

Исследовался абразивный круг 23A-80-K5-VBE (абразив алун — дум 23А зернистостью 80, твердостью К, структуры 5 на керами­ческой связке VBE) диаметром 305 мм и шириной 51 мм. Правка круга производилась монокристаллом алмаза в 1 карат, имеющим радиус при вершине примерно 0,75 мм. Номинальный размер зерен

Таблица 26 Условия правки Номер опыта Продольная подача, мм/сек Поперечная подача алмаза, мкм Частота, соответствующая шагу правки, гц і 0,43 5 29 2 1,29 7,5 9,75 3 5,8 13 2,18 4 12,9 18 0,975 5 0,43 5 29 6 1,29 7,5 9,75 7 5,8 13 2,18 8 0,43 7,5 29 9 9.5 38 1.3 Примечание. Анализ проводился для условий правки опытов 4 и 8; опыты 4 и 8 рас­сматривались соответственно как «грубая» и «тонкая» правки: скорость вращения круга прини­малась равной 1750 об/мин.

шлифовального круга составлял 0,2 мм. При каждой правке выпол­нялось 3 прохода с режимами, указанными в табл. 26, а также 1 проход без поперечной подачи. Правка производилась с охлажде­нием водно-масляной эмульсией, содержащей 7% масла.

После каждой правки анализировалась топография поверхности шлифовального круга и записывались величины функций ФПВ, ФИР, АФ при измерении обоими датчиками.

Из табл. 26 следует, что правка производилась в пяти различ­ных условиях. Диапазон этих условий ограничивался продольной подачей 0,43 мм/сек и поперечной подачей 5 мкм, с одной стороны, и соответствующими значениями 12,9 мм/сек и 18 мкм — с другой. Этот диапазон рассматривался как реальный для условий правки на практике. В таблице приведены также частоты, соответствующие шагу правки, т. е. отношению продольной подачи к скорости вра­щения круга для различных условий правки.

Для исследования поверхности, претерпевшей значительные изменения, круг был специально засален путем грубой правки с последующим шлифованием в соответствующих условиях.

Проведенное исследование можно подразделить на три основ­ных этапа:

1. С применением щупового датчика при низкой скорости. Щуп перемещался относительно неподвижной поверхности шлифо­вального круга в осевом направлении со скоростью 0,43 мм/сек при различной глубине проникновения щупа в поверхность круга.

2. С применением оптического датчика при низкой скорости. Датчик с оптическими волокнами перемещался так же, как и щу — повой, т. е. относительно неподвижного круга в осевом направлении 0,43 мм/сек. Зазор между торцом датчика и поверхностью круга составлял около 350 мкм.

3. С применением оптического датчика при высокой скорости. Круг вращался со скоростью 29 об/сек (1740 об/мин) для получения комбинированной развертки в осевом и круговом направлениях.

Для получения требуемого диапазона усиливаемых частот (например, до 200 гц) для высокоскоростных испытаний был приме­нен модифицированный осциллоскоп Tektronix 564В в сочетании с усилителем Tektronix ЗАЗ. При этом получаемый выходной сигнал был эквивалентен сигналу на экране катодно-лучевой трубки. В этом случае осциллоскоп можно было использовать в качестве уси­лителя. Функции ФПВ и ФИР, а также АФ были записаны при всех трех указанных сериях испытаний.

Теория корреляции была разработана главным образом при­менительно к сигналам, имеющим распределение высот, соответству­ющее кривой нормального распределения Гаусса. Спектр для вы­бранной АФ был получен преобразованием Фурье с помощью ком­пьютера KDF9.

Результаты экспериментов по анализу ФПВ, полученные при измерениях щуповым датчиком на глубине 25 мкм при низкой ско­рости перемещения, представлены на рис. 108, а.

Концентрация неровностей в наружном слое шлифовального круга (кривая 1) в условиях тонкой правки (круг имеет более гладкую поверхность) выше, чем в условиях грубой правки (кри­вая 3). В условиях грубой правки концентрация неровностей в наружном слое ниже и неровности эти менее плоские. В случае затупления круга, предварительно подвергнутого грубой правке, ФПВ приближается к этой функции для круга, подвергнутого тонкой правке, что объясняется заглаживанием неровностей ПС в процессе его износа и засаливания. Таким образом, поверхность круга после правки может быть эквивалентна поверхности засален­ного круга.

Графики ФИР (или кривые опорной поверхности), соответству­ющие рис. 108, представлены на рис. 109. Поскольку при отсутствии контакта щупа с абразивными зернами сигнал со щупа нулевой, кривые ФИР позволяют определить долю расстояний между зернами по величине, на которой кривая пересекает ординату нулевой высоты.

Кривые АФ, соответствующие условиям, указанным примени­тельно к рис. 108, а, представлены на рис. 110. Анализ этих функций показывает, что разность в длине корреляции, как и было уста­

новлено в работе Пекленик, очень мала. Концевые части кривых, выражаемых этими функциями, указывают на наличие периодиче­ской составляющей, которая более явно выражена пиком на графиках функций спектральной плотности, показанных на рис. 110. Анализ кривых на этом рисунке показывает, что в случае грубой правки

Рис. 108. Кривые ФПВ (а) и ФИР (б) при измерении поверхности круга щу — повым методом: 1 — тонкая правка; 2—изношенный круг; 3 — грубая правка.

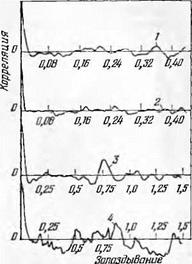Рис. 109. Кривые АФ, полученные с
помощью щупового и оптического дат-
чиков:

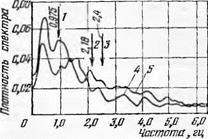1 — тонкая правка (щуповый датчик); 2 —
грубая правка (щуповый датчик); 3 — тон-
кая правка (оптический датчик); 4 — гру-
бая правка (оптический датчик).

Рис. ПО. Плотность спектра при изме-
рениях щуповым датчиком (разрешаю-
щая ширина полосы 0,334 гц; глубина
развертки 25 мкм):

/ — правка, частота 0,975 гц; 2 — прав-
ка, частота 2,18 гц; 3 — зерно, частота
2,4 гц; 4 — тонкая правка; 5 — грубая
правка-
круга спектр имеет больше изменений, чем можно было ожидать
(очевидно, из-за более заостренных неровностей).

Поверхности, подвергнутые развертке с помощью щупового датчика, были также развернуты с применением оптического дат­чика для получения ФПВ (рис. 111, а). Приведенные кривые, счи­тают авторы работы [99], близки к кривой нормального распреде­ления Гаусса. Круг, подвергнутый грубой правке, характеризуется большим средним значением и большей дисперсией, чем круг, под­вергнутый тонкой правке. Грубо правленный круг, затупившийся при последующем шлифовании, характеризует ФПВ, смещенную в направлении нулевой координаты. Средняя величина при этом мень­ше, чем в случае тонкой правки круга, а дисперсия больше, чем для
круга, подвергнутого грубой правке и еще не затупившегося. По­следние явления авторы этой работы связывают с изменением отражательной способности зерен из-за засаливания круга, приво­дящего к изменению окраски.

Высокая концентрация неровностей при уменьшенной амплиту­де их объясняется наличием более темных и более плоских зерен и меньшими предельными верхними величинами, что связано с тем, что зерна сохраняют свой цвет при возможном раскалывании.

Рис. 111. Результаты измерений оптическим датчиком при низкой скорости: а — ФПВ высоты неровностей (ординаты); б — плотность спектра; I — изношенный круг; 2 — грубая правка; 3 — тонкая правка.

На рис. 109 показаны АФ, соответствующие тем же условиям тонкой и грубой правки круга, которые указаны на рис. 111 для измерения оптическим датчиком. Различие в длине корреляции для различных условий правки здесь также незначительное. Боль­шая дисперсия для круга с грубой правкой может быть определена непосредственно из АФ измерением величины корреляции при нуле­вом запаздывании.

Преобразование АФ позволяет оценить спектральную плот­ность (см. рис. 111, в). Анализ его вновь указывает на большее отклонение в спектре и более высокие частоты, которые имеются в случае грубо правленного круга. Однако в этом случае невозмож­но непосредственно установить, в каком случае имеются пиковые значения, поскольку оптический датчик создает сглаживающее действие, из-за чего частоты снижаются примерно в 4 раза.

На рис. 112, а показаны графики ФПВ для шлифовального круга с грубой правкой до и после износа. Опыты проводились со шлифовальным кругом, вращающимся со скоростью 1750 об/мин при осевом перемещении датчика относительно рабочей поверхности круга. Представленные кривые были рассчитаны с помощью корре­лятора, работающего в форме ас (т. е. при нулевой средней величи­не), поскольку все частоты были выше нижней предельной частоты датчика 1 гц.

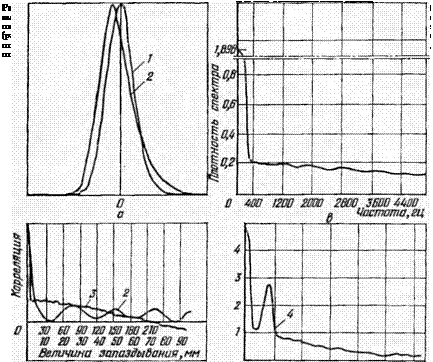
Анализ кривых показывает, что шлифование приводит к отри­цательному смещению распределения, что объясняется, помимо других возможных факторов, некруглостью шлифовального круга.

Результаты этих опытов позволили определить АФ для грубо — правленного круга до и после его засаливания (рис. 112, в). Отчет­ливо различимая периодическая составляющая кривой АФ, соот­ветствующая засаленному кругу, является следствием выступов на поверхности круга, образующихся в процессе шлифования. Со­ответствующая кривая плотности спектра представлена на рис. 112, в, г, причем пик на кривой (рис. 112, г) является следствием выступа на круге. Расчеты, основанные на периоде, соответствую­щем этому пику, показывают, что на периферии круга образовалось 60 таких выступов.

Для определения влияния типа в спектре, соответствующем частоте размера зерна, полученном для круга зернистости № 80

в опытах с низкой скоростью, был произведен расчет кривых плот­ности спектра для кругов зернистостью № 46 и 150. Полученные таким образом кривые также имели высокие пики в спектрах. Причем эти пики находились вблизи частот, соответствующих ша­гам правки, принятым в опытах. Это свидетельствует о том, что состояние поверхности круга до шлифования имеет существенное значение.

Были сделаны попытки увязать результаты, полученные в опы­тах с щуповым датчиком, с результатами измерений оптическим датчиком при перемещении его относительно абразивной поверх­ности с высокой и низкой скоростями. При вероятностных измере­ниях это труднее выполнять, чем при корреляционных. Это объяс­няется главным образом тем, что оптический датчик обозревает более ограниченную площадь поверхности, и поэтому участие неровностей непосредственно ПС в общем выходе сигнала незна­чительно.

По-видимому, щуповый датчик дает результаты, наиболее близ­кие к реальным, поскольку им измеряются только неровности ПС, которые принимают участие в процессе шлифования. Поэтому результаты измерений оптическим датчиком можно рассматривать лишь как приближение к результатам измерений щуповым датчи­ком. Данные приведенного исследования свидетельствуют о том, что оптическая система является чувствительной к изменениям топографии поверхности шлифовального круга. Однако такая си­стема не может в полной мере выявить изменения в топографии круга при грубой и тонкой правке.

Вибрации шлифовального станка создают периодическую со­ставляющую на поверхности шлифовального круга как во время правки, так и при развертке этой поверхности при высоких скорос­тях. Влияние этого фактора в дальнейшем будет учтено, получен­ные результаты будут способствовать лучшей оценке плотности спектра.

В итоге авторы работы [99] приходят к заключению, что приме­нение оптических и щуповых датчиков с применением теории ста­тистики и корреляции показало возможность обнаружения измене­ний в топографии абразивной поверхности.

Данные, полученные с использованием оптического датчика, совпадают с данными при использовании щупового датчика. Таким образом, измерение неровностей на поверхности шлифовального круга является технически возможной задачей. Высокоскоростные опыты, проведенные с применением оптического датчика, показа­ли, что он способен детектировать как некруглости круга, так и засаливание его поверхности. Вместе с тем результаты опытов не позволили в полной мере выявить различия в топографии поверх­ности при различных условиях правки круга. Потенциальные воз­можности оптических датчиков в области измерения поверхности шлифовального круга выявлены еще не в полной мере. Требуются дальнейшие исследования.