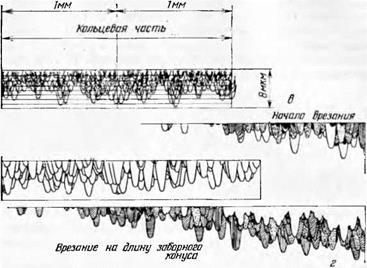
Графическая модель абразивного слоя шлифовальных инструментов

Графическая модель абразивного слоя для правящего ролика, оснащенного АСК 250/200 в двух проекциях, изображена на рис. 34. Построение ее производилось следующим образом. Методом царапа­ния клина определялся закон разновысотности зерен по глубине слоя (в данном случае до ht = 16 мкм) в расчете на базу шириной 1 мм. На развертке кольца диаметром 60 мм и шириной 1 мм наноси­лась сетка с шагом по ширине 0,05 (20 элементарных полос, Дb = = 0,05 мм). Длина окружности была разбита на 200 участков,

шаг между которыми составлял = 0,942 мм ~ 1 мм. При

определении местоположения зерен в поперечном сечении высота ht = 16 мкм была разбита на восемь линий с шагом 2 мкм.

Таким образом, для построения графической модели была создана объемная (пространственная) решетка, состоящая из 20 X X 200 x 8 = 32 000 элементарных объемов с размерами 0,002 х X 0,05 х 0,942 мм3, в которые, используя метод Монте-Карло (метод случайных чисел), помещали вершины абразивных зерен.

Заполнение элементарных объемов вершинами зерен произ­водилось последовательно по интервалам глубины 0—2; 2—4 и 4—6 мкм и т. д. Так, на основании обработки профилограмм царапин на клине (см. образен профилограммы на рис. 24) было установлено, что в интервале 0—2 мкм имеется одно зерно.

С помощью извлечения нумерованных шариков из урны было установлено, что это зерно, которому был присвоен номер /, раз­мещается по ширине ролика на 10-й линии, по длине окружнос­ти — на 44-й линии.

На поперечной проекции в середине интервала 0—2 мкм вычер­чивалась окружность вершины зерна / диаметром d{, = 0,2 мм (в данном случае вершина эллипса в связи с разностью масштабов по высоте и ширине сече­ния). В интервале 2—4 мкм В 24 Б6Ю12141Б18 20 по царапинам было установ­лено наличие двух зерен (2 и 3), которые случайным образом разместились на соседних 12-й и 13-й лини­ях по ширине и на 4-й и 65-й линиях по длине роли­ка. Аналогичным образом были «разыграны» все ос­тальные зерна (всего на глу­бине 16 мкм их было 44 шт.).

Графическая модель в наиболее простой и нагляд­ной форме может проиллю­стрировать объемное строе­ние наружного рабочего слоя, образованного высту­пающими над связкой аб­разивными зернами.

Из рассмотрения проек­ции зерен в поперечной плоскости (четырехуголь­ник 1 X 0,016 мм2) устанав­ливаем, что наиболее непе — рекрытыми зернами по вы­соте являются зерна /; 4;

6; 7, которые будут рабо­тать как прорезные резцы.

Частичное перекрытие зерен начинается уже в интервале 2— 4 мкм, где проекции зерен 2 и 3 накладываются друг на друга по ширине. Внешний неперекрытый контур образуют зерна (слева направо) 14; 8; 4; 9; 12; 6; 31; 1; 2; 3; 10; 25; 7; 12; 24; 29, что и за­фиксировано профилограммой на клине. Остальные зерна вычисля­лись методом экстраполяции параболической кривой, как это по­казано на рис. 24, б.

Нижняя, горизонтальная проекция позволяет судить об очеред­ности расположения центров вершин зерен по длине развернутого цилиндра и о количестве зерен, расположенных на одной окружности • вращения. 1

Так, устанавливается, что на линиях 7-й и 9-й вершины зерен отсутствуют, в то время как на линиях 10-й и 17-й сосредоточено по пять зерен. Наибольшее число окружностей имеют одно зерно или два, что коррелирует с данными табл. 11.

Рассмотрим механизм образования срезов при врезном шлифова­нии (при вращении развертки цилиндра слева направо), например для элементарной окружности, на которой расположены последо­вательно зерна 20; /; 26; 17 и 43. Так, зерно 20, предшествующее зерну 1, прорежет предварительно канавку, а зерно 1, расположен­ное на дуге вращения непосредственно за зерном 20 и существенно выше его (на 10 мкм), прорежет более глубокую канавку, и след от работы зерна 20 не останется на обработанной поверхности, они исчезнут, хотя зерно 20 было рабочим зерном.

Совершенно ясно, что зерно 26, находящееся непосредственно за зерном 1, расположенное глубже зерна 20, полностью экра­нируется своим предшественником и попадает в прорезанную канавку. Резать оно может случайным образом, если, например, металл из канавок, образованных зернами на соседних (расположен­ных справа и слева) окружностях вращения, не вытеснится после прохождения зерна 1 на траекторию движения зерна 26. В данном случае этого не происходит и зерно 26 выпадает из процесса работы.

Как будут вести себя последующие зерна 17 и 43, заранее нельзя предусмотреть. Это зависит от длины прорезания зерном 1 канавки. Если при определенном значении К2 длина царапины от зерна 1 закончится ранее, чем вступят в работу зерна 17 и 43, то они оба или одно из них будут режущими.

Если изменить направление вращения на обратное, то для той же окружности вращения режущими зернами могут быть после­довательно зерна 43; 17 и /, а заэкранируется зерно 20. При этом может наблюдаться полное или частичное расширение канавки, образованной вначале зерном 43, затем возвышающимися зернами 17 а 1. Поведение зерна 26, расположенного между более высокими зернами 17 и 1, здесь неопределенное. Наиболее вероятно, что оно будет заэкранировано предшествующим зерном 17.

Как видно из проекции развертки цилиндра вращения, ни о каком равномерном распределении вершин зерен на поверхности круга не может быть и речи. Количество зерен, попадающих на площадку So, соизмеримую со средними расстояниями между зер­нами, может быть оценено лишь вероятностным путем на основании распределения Пуассона случайных величин в области D.

Графическая модель абразивного слоя позволяет наглядно продемонстрировать форму и размеры теоретического среза, а также • непосредственно выделить режущие зерна из общего коли­чества зерен в слое.

Для дальнейших построений в качестве графической модели был выбран торцовый чашечный круг, поперечная форма кольца которого имела рабочий заборный конус с углом профиля ср и длиной /г = 3 мм, цилиндрической поясок длиной £>0=1 ММ V

обратный конус с углом ф, и длиной /2 — 1 мм. По методике, из­ложенной выше, было произведено вероятностное распределение вершин зерен в сетке, состоящей из элементарных объемов с раз­мерами 0,001 X 0,05 X 0,385 мм.

Здесь разбивка слоев по вертикали была произведена через 1 мкм, а развертка длины кольца круга диаметром 125 мм и шириной 5 мм (по среднему диаметру 122,5) была разбита на 1000 частей.

За прототип модели был принят круг из КНБ зернистостью КО 125/100-150%, с помощью которого были получены ранее струж­ки при шлифовании стали Р18, распределение которых представлено на рис. 31 и 32.

Графическая модель такого круга представлена на рис. 35. Взаимное расположение вершин зерен на заборных и цилиндрической частях рабочего кольца круга показано до глубины ht = 8 мкм, рав­ной глубине резания (рис. 35, а). После придания кругу вращения и подачи So6 = 0,312 мм/об определилось кинематическое наложе­ние зерен друг на друга (проекции зерен показаны на рис. 35, б).

На заданной глубине в резании участвуют заборная часть дли­ной 1=2 мм, цилиндрическая (зачистная) часть шириной b() = 1 мм и отдельные зерна обратного конуса.

В результате совокупности движения вращения и продольной подачи образуется так называемый кинематический заборный конус с углом фЛ, меньшим по величине угла конуса ф, измеряемого на круге в статическом состоянии вследствие удлинения конуса на величину, равную So6-

При построении проекции зерен на кинематическом конусе учитывалась траектория движения каждого отдельного зерна в зависимости от положения его на окружности вращения.

Продольное смещение зерен вдоль подачи AS і рассчитывалось

по формуле A Si = So6—4—, где lt — дуговое расстояние данного

*“*Кр

зерна по окружности вращения от начальной точки отсчета.

На рис. 35, в, г, д показана последовательность врезания кине­матической модели в деталь. Устанавливается, что при одном акте врезания (за один оборот круга) не весь металл снимается с детали, а для врезания всего заборного конуса требуется несколько оборотов круга (рис. 35, д).

Общий характер формы и поперечного сечения срезов показан на схеме рис. 35, д (отдельные обороты круга выделены одинаковой интенсивностью зачернения). Здесь показан эффект дополнитель­ного врезания круга на величину hJ2, максимальная глубина ре­зания (с учетом величины шероховатости) показана равной Лтах = = 11,5 мкм.

После нескольких оборотов графической модели круга опре­делились форма и расположение теоретических срезов и был удален срезанный металл. Здесь (рис. 35, е) показаны оставшиеся попереч­ные неровности обработки (шероховатость поверхности) при прямом (правая часть рисунка) и обратном ходе, в результате чего шерохо-

ватость уменьшилась (левая часть рисунка). На рис. 35, ж показан профиль шероховатостей, которые могут быть описаны дугами ок­ружностей переменного радиуса р, зафиксированных с помощью профилограммы при реальном шлифовании пластины.

На рис. 36, который повторяет исходную графическую модель рабочего слоя в статическом положении рис. 35, а, штриховкой по­казаны режущие зерна, участвующие в работе. Устанавливается,

картина врезания зерен; форма среза и профиль неровностей при прямом и об — плоской пластины.

что они располагаются на всю глубину шлифования (ht = 8 мкм) на заборной и цилиндрической (зачистной) части круга, и только несколько зерен участвуют в работе на заборной части обратного конуса.

Это еще раз подтверждает мысль о том, что зерна на заборной части не срезают полностью весь металл, а оставляют его для сре­зания зернами зачистной кромки. Наибольшая плотность режущих
зерен приходится на участок стыковки конуса и зачистного пояска, в результате в этой части кольца износ происходит относительно интенсивнее, со временем возрастает длина 1Х заборной части и умень­шается длина участка Ь0. При сокращении длины Ь0 до минимума степень износа становится максимальной и величина Ь0 начинает вновь возрастать, сокращая величину 1г и увеличивая угол <р.

1мм 1мм 1мм

Рис. 36. Расположение режущих зерен на графической модели круга ЧК, оснащен­ного КНБ зернистостью 125/100 150%-ной концентрации.

Динамика изменения /, и Ь0, углов <р и q>j описана в работе [5] на основе прямых экспериментальных измерений элементов попереч­ного профиля шлифующего кольца торцового круга (круга типа чашек).

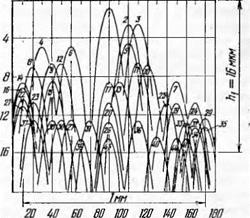
На рис. 37 показан характер параболического нарастания общего числа зерен круга, определенный по профилю царапин,

оставленных на плоской пластинке при радиальном врезании зерен круга из КНБ 125/100 150%-ной концентрации на рассматриваемую глубину (ht = 7 -~ 4- 8 мкм) на базе измерения В = 3 мм (круглые точки).

По отношению к этой же кривой крестиками показано распределение по глубине числа режущих зерен, взя­тых из графической модели рис. 36. Число режущих зерен хорошо аппро — Рис. 37. Выделение режущих зе — ксимируется прямой, касательной к рен 2реж из общего числа зерен параболе изменения общего числа зе — в слое Zo6lu с помощью обработ — Рен в точке А0 = 3 мкм. ки данных, полученных на гра — Таким образом, графическая объем — фических моделях абразивного ная модель рабочего абразивного кру­той — га позволяет: воспроизвести пол­

ностью процесс срезания металла каждым зерном; определить форму и распределение теоретических срезов в поперечной плоскости (боковой плоскости обрабатываемой пластинки); выделить из общего числа режущие зерна и найти закон распределения их по глубине слоя; найти плотность и ха­рактер распределения режущих зерен на конической и заборной частях инструмента.

Имитация процесса шлифования с помош. ью графической моде­ли круга наглядно и просто подтвердила методику выделения ре­жущих зерен с помощью касательной к кривой параболической

функции Zi = ah2, обоснованную в работе [12] на основании изу­чения линейного характера изменения сил и удельного износа алмазов в функции глубины шлифования.