Форма среза и стружки при правке и шлифовании

При рассмотрении кинематики было установлено, что на пер­вом этапе врезания царапины вдоль окружности шлифуемого тела не сливаются. В этом случае продольное сечение канавки, обра­зованное врезающейся вершиной зерна (см. рис. 26), практически симметрично и при развертке окружности может быть отождествлено с сегментом круга, дуга которого «вписана» в канавку. Форма

поперечного сечения среза подобна форме контура неперекрытой режущей части вершины зерна. Неперекрывающиеся зерна работают как прорезные резцы, т. е. осуществляют резание и боковыми сто­ронами вершины резца (двухкромочное резание). Для зерен, рабо­тающих на глубине РПС, начиная от точки h0 и глубже, поперечное сечение уменьшается из-за все нарастающего перекрытия вершин друг другом (картина поперечных срезов схематично представлена на рис. 23).

Среднее сечение среза, приходящееся на расчетные зерна, вследствие линейного нарастания числа режущих (неперекрытых) зерен по глубине шлифования будет постоянным. Величина фак­тического сечения, приходящаяся на каждое поперечное зерно, существенно отклоняется от средней и может быть оценена распре­делением Пуассона. Для этой группы зерен резание будет одно­кромочным, так как осуществляется только небольшой частью не — перекрытого контура вершин с площадью среза, существенно мень­шей, чем для прорезных зерен. Причем размеры среза (ширина и толщина) будут инвариантными по отношению к избранным ко­ординатам отсчета. В связи с этим распределение толщины среза и ширины среза равным образом может быть оценено по преобразован­ному нами уравнению Пуассона (1.44). Продольную форму среза для фазы установившегося шлифования можно уяснить из рис. 27—29.

Рассмотрим форму среза в случае образования звездочки при целом числе царапин, укладывающихся по длине окружности шли­фуемого тела (в нашем примере шлифовального круга, обрабатывае­мого правящим роликом). Продольный срез будет равномерным по толщине, а по длине (измеренной по дуге окружности круга) он

будет

В случае дробного значения величины Кг на окружности круга будут укладываться некоторое целое количество срезов длиной /ц и дробная часть /ц. В результате центры царапин, расположенные на последующих спиралях, сместятся на эту дробную часть, про­дольная форма среза изменится и высота среза будет неодинаковой. На нем в верхней части появится точка, образуемая пересечением двух траекторий движения смежных вершин зерен. Образуется дву — запятообразная стружка (с «горбом»). Слева и справа от точки соеди­нения этих двух запятообразных частей толщина стружки по­степенно падает до нуля.

Оценим для Кг = 1,2 соотношение между длиной и толщиной среза (см. табл. 10). Для ролика диаметром 70 мм при К3 ~ 5 в случае группы I : /ц = nd_/C3IU = 3,14 • 70 • 5 ■ 0,1 = 110 мм, К = 2,55об.

При правке подача на один оборот ролика редко бывает более 10 мкм, тогда Лц = 0,025, а соотношение /ц : /іц = 4,4 • 103.

Таким образом, для верхних прорезных зерен, число которых на одной окружности мало (в нашем примере их всего четыре), длина царапины по сравнению с глубиной на 3—4 порядка больше.

Если на одной окружности ролика уложить 220 шт. алмазов (с шагом 1 мм), то для группы I (см. табл. 10) длина царапины

составила бы /ц= ^ 4 «= 2 мм, а /ц : Ли = 80, т. е. практически

на 2 порядка выше. Очевидно, при такой длинной и тонкой стружке не следует учитывать неравномерности ее размеров по длине и для практических расчетов удобнее оперировать ее усредненной тол­щиной по уравнению (1.37).

При передаточном отношении К2 =1,04 размеры среза меньше различаются. При группе IV имеем /ц = 3,14 • 70 • 5 — 0,01 =

= 11 мм, Лц= 0,25 мм и /и : Лц = 44. При Z0 = 220 шт. /ц = 1 —

= 0,2 и /ц /гц. Поскольку подача S0c>= 10 мкм/об встречается ред­ко (в большинстве она равна 1 мкм/об и менее), то всегда /ц /іц. В этих условиях трудно свести «боковую» площадь среза к запятообразной форме, характерной для схемы продольного фре­зерования.

Какова будет форма стружки для шлифования детали, в усло­виях, КОГДа ПКр > Цдет и £>кр > Йдет?

Обратимся к рассмотренному нами ранее примеру. При К2 = 5 и Z0 = 4 шт. царапины имели длину /ц =3,14 • 100 • 0,05 = = 15,7 мм; при врезании с подачей So6 = 1 мкм/об hu = 5So6 = = 0,005 мм и /ц : Лц = 3,14 • 103.

Таким образом, для того, чтобы длина и толщина стружки при шлифовании были одного порядка, необходимо иметь на одной окружности сотни и тысячи зерен. И в данном примере имеется мало оснований сводить продольный срез к форме запятой.

При рассмотрении стружек под микроскопом, особенно после шлифования алмазным инструментом, обращает на себя внимание близость их формы к форме стружек, образуемых токарными рез­цами при продольном точении. В стружках шлифования наблюда­ется нередко текстура, образованная в результате пластического сдви­га слоев металла, характерного для образования сливной стружки.

Итак, для абразивного инструмента, у которого распределение зерен по длине окружности подчиняется закону Пуассона, распре­деление размеров среза по ширине и толщине из-за равновероят­ности расположения поперечного сечения среза по отношению к системе координат должно определяться уравнением Пуассона (1.44), а длина среза определяется не только числом и законом рас­пределения зерен на окружности вращения, но и кинематическими соотношениями Кг, К2 и Ка. В связи с этим она должна рассчитывать­ся на основе кинематических взаимосвязей шлифующего инструмен­та и обрабатываемой детали.

К сожалению, не имеется возможности экспериментально из­мерить форму среза, поэтому эти срезы называют расчетными, теоретическими. В распоряжении экспериментатора имеются лишь результаты превращения срезов в продукты диспергирования — осколки хрупких веществ и стружку пластически деформируемых
материалов. В качестве основы для косвенного анализа могут быть использованы следы обработки — поперечные и продольные не­ровности, а также распределение зерен на окружности вращения.

Распределение расстояний между зернами было использовано нами для экспериментального доказательства существования урав­нения (1.44), графическое выражение которого показано на рис. 17.

При анализе распределения размеров стружки необходимо иметь в виду влияние двух факторов: пластическое искажение формы среза в результате явлений усадки стружки и неполное удаление металла из прорезаемой канавки, связанное с вытеснением

его на боковые стороны.

Эти факторы приводят к тому, что доля толстых стру­жек в общем характере рас­пределения ширины или тол­щины стружек по сравнению с теоретическим распределе­нием срезов по уравнению Пу­ассона (1.44) возрастает, в ре­зультате чего кривая распре­деления размеров стружек не совпадает с кривой распреде­ления размеров срезов (см. рис. 18). Эти искажения при­водят к относительному сни­жению высоты моды распре­деления и увеличению вероят­ности появления утолщенных срезов по сравнению с расчетными по уравнению Пуассона (несов­падение экспериментальных данных с положением правой части кривой уравнения (1.44)).

Заранее можно сказать, что для высоких скоростей шлифо­вания, для которых степень усадки и вытеснения металла из ка­навки меньше, кривые распределения срезов и сечений стружки будут несущественно отличаться друг от друга.

Не совпадает и левая ветвь уравнения (1.44) с кривой экспери­ментального распределения мелких стружек. Причина заключается в том, что при малых толщинах среза прорезается только канавка без отделения стружки. Поэтому существует граница (линия а—а на рис. 18), ниже которой стружкообразование при данной скорости резания невозможно. С увеличением скорости шлифования эта гра­ница сдвигается влево, экспериментальная и теоретическая кривые сближаются.

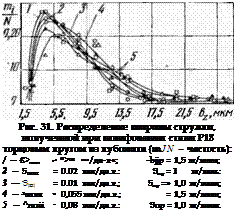
Для иллюстрации указанного на рис. 31 приведены кривые экспериментального распределения сечений срезов, полученные в работе [5] при торцовом шлифовании быстрорежущей стали на скорости 20 м/сек кругами ЧК 125 X 5 X З X 32 м, оснащенными по­рошком кубического нитрида бора зернистостью 125/100, 150%-ной

концентрации на органической связке В1. На рисунке показано совмещение кривых распределения ширины стружки для пяти режимов резания, подачи при которых изменялись в поперечном направлении 8 раз (0,01—0,08 мм/дв. ход), и в продольном в 1,5 раза (1,0—1,5 м/мин). Однако экспериментальные точки вполне удовлет­ворительно с небольшим рассеиванием располо­жились по отношению к некоторой общей кривой распределения, у кото­рой &min = 2,5 мкм (тео­ретическое значение сре­за fcmin 0), модальное значение эксперимен­тального распределения тяготеет к вероятности 0,25 (теоретически Рмод=

= 0,368), а вероятности появления широких стру­жек несколько выше рас­четных значений (см. точ­ки на рис. 18).

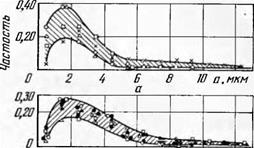
Аналогичную карти­ну наблюдаем на рис. 32, а и б, где показан харак­тер распределения тол­щины и ширины среза при изменении глубины резания в 50 раз (с 0,01 до 0,5 мм дв. ход). Экс­периментальные точки здесь также тяготеют к общей кривой распреде­ления.

Отметим размах вари­ационного ряда: атт т* Птах — 0,5 і 13 МКМ (Птах/Птіп “ 26), Йтіп “Г" ах 2,5 ~г~ 27,5 МКМ (Йпіах/^п:іп ==s 11). ЛІО — дальные значения амод = 1,75 мкм; Ьшш = 5 мкм, среднее значе­ние пср = 2,9 мкм; Ьср = 8 мкм.

На рис. 32, в показано распределение сечения стружки /стр = = ab (/mi,, = 1 мкм2; /тах = 190). Причем среднее значение сечения стружки /ср = 25,4 мкм2 2,9 ■ 8 = 23,2 мм2. Здесь модальная частость приблизительно равна сумме частостей модальных значений толщины и ширины стружки.

Обращает на себя внимание возможность срезания зернами КНБ существенно малых по размерам стружек. Учитывая значитель­ную усадку тонких срезов (очевидно, превышающую 2), можем

констатировать возможность среза металла толщиной в десятые доли микрометра. Столь малые срезы не удается получить в экс­периментах по царапанию отдельными зернами или инденторами правильной формы (конусом или пирамидой). Очевидно, из-за малой жесткости системы СПИД в последнем случае индентор при малых сечениях выходит из-под стружки. Усилие на нем не в состоянии выбрать зазоры и создать достаточное для установив­шегося резания равновесие между силой резания и усилием натяга в системе. Поэтому резание удается осуществить с глубиной, на 1—2 порядка большей.

Очевидно, в силу указанных обстоятельств утвердилось мне­ние, что отделение стружки от металла возможно лишь тогда, когда толщина среза будет соизмерима с величиной радиуса ок­ругления режущих кромок зерна р. По данным, например, работы 196] величина р для эльбора в среднем составляет 6—10 мкм, а при полировании свободным абразивом, когда искусственно созда­ется давление на полировальнике, как было принято в работе [43], срезание стружки возможно при отношении глубины среза к радиусу округления Ыр >- 0,5. Если принять этот постулат за исходный, то в наших опытах минимальная толщина среза не долж­на была быть менее 3—5 мкм, т. е. должна быть на целый порядок больше наблюдаемых толщин среза. Очевидно, в практическом шли­фовании ограничения по толщине среза не существенно зависят от радиуса округления режущих кромок, и объясняется это иной схе­мой стружкообразования по сравнению с классической, основанной на схеме образования стружки режущим клином с передней и задней гранями и радиусом р округления режущей кромки, базирующейся на схеме простого (плоского) сдвига срезаемого материала в одной плоскости (или зоне) деформации.

При шлифовании, как следует из рис. 31 и 32, имеются пре­дельные толщины среза, ниже которых невозможно стружкоот — деление, но они связаны не только и не столько с геометрическими параметрами режущего зерна, сколько с характером течения плас­тически деформированного объема по боковым сторонам нижней час­ти (контактируемой части) зерна и со скоростью этого течения.

При недостаточной скорости выдавливания объема из канавки материал не отделяется от основы и стружка не образуется. Поэтому при высоких скоростях шлифования возможно превращение в стружки срезов весьма малых толщин без валиков на боковых сто­ронах прорезанной канавки [36].

Совпадение распределений размеров стружки для различных значений произведений подач Snp Snon свидетельствует о независи­мости сечений среза, приходящихся на зерна, от глубины шлифова­ния. Это возможно, как доказывалось в работе [12], если при линей­ном увеличении глубины среза число режущих зерен, вводимых шлифовальным кругом, также изменяется по линейному закону. Однако одного этого условия недостаточно; необходимо, чтобы в по­перечном сечении (по уровням высоты) зерна располагались по одно-

му закону, в данном случае по закону Пуассона, параметр которого» а = Kli изменяется пропорционально ширине среза 1С при средней равномерной плотности распределения зерен на единице длины *-■= Si-

Итак, при шлифовании пластичных металлов образуется набор стружек самых разнообразных размеров и форм:

а) стружка из сегментообразного среза (из перекрывающихся или неперекрывающихся по длине царапин) для самых верхних прорезных зерен при первой фазе врезания;

б) стружка установившейся формы (равномерная по толщине или двузапятообразная) при второй фазе шлифования для зерен, расположенных глубже прорезных (неперекрытых);

в) стружка, приближающаяся к запятообразной, для наиболее глубоко и наиболее часто расположенных на одной окружности вращения зерен в зависимости от величины /(2;

г) стружка смятия, гофрированная или переменного сечения и формы, образуемая разрушающимися абразивными зернами во время прорезания канавки;

д) стружка подгорелая, оплавленная и термически деформи­рованная вследствие высоких температур шлифования.

Очевидно, сведение формы стружки к одной запятообразной, для которой рядом исследователей выведены формулы [54], не от­ражает действительной картины стружкообразования.

При шлифовании хрупких веществ материал царапин диспер­гируется на очень мелкие осколки. Изучение этих осколков не позволяет судить о величине фактического среза, приходящегося на зерна шлифующего инструмента.

При правке шлифовального круга наибольший интерес пред­ставляет изучение последствия взаимодействия зерен алмазов с зернами абразива, которые подвергаются раскалыванию и удалению из поверхностного слоя, в результате чего возобновляются его режущие свойства.

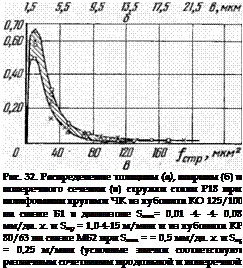
Распределение осколков шлама, образованного при правке круга алмазным роликом, достаточно полно освещено в работе [12]. Отметим, что это распределение не зависит от изменения величины поперечной и продольной подачи и описывается уравнением (1.44). Обработка экспериментальных данных работы [12] по уравнению Пуассона приведена на рис. 33. Здесь сплошная линия представ­ляет теоретическое распределение Пуассона, а экспериментальные точки — распределение (гранулометрический состав) осколков зерен абразивных кругов на керамической связке твердостью СМ1-СМ2, зернистостью 16, 25, 40. Режим правки: скорости вращения круга и ролика цкр = 30 м/сек; vp = 4,5 м/сек (вращение встречное), Snp = 1 — т — 2,5 м/мин; Snon = 0,005 0,02 мм/ход при правке

методом продольных проходов и Snon = 0,25 1,0 мм/мин при

правке врезанием. Правка производилась алмазными роликами АСК 200/160, АСК 250/200 и АСК 500/400 различной зернис­тостью.

Как видно из рис. 33, несмотря на разнообразные условия правки и различ­ную зернистость абразив­ных кругов и правящих роликов, эксперименталь­ные точки вполне удовле­творительно расположи­лись по отношению к нор­мированной кривой распре­деления Пуассона. Этого и следовало ожидать, так как правка производилась в одинаковых кинематиче­ских условиях, т. е. при сохранении практически постоянными значений К, и К2 и относи­тельно небольшом изменении в опытах диаметра круга (Ks остава­лось практически постоянным). В этих условиях относительно по­стоянными сохранились значения величин срезов (формы стружки), косвенным проявлением чего явилось относительно одинаковое рас­пределение размеров шлама.