Экспериментальное определение характера распределения и количества вершин зерен в поверхностном слое инструмента

Для нахождения закона распределения вершин зерен в ПС инструмента необходимо спроектировать их во время вращения круга на плоский экран, например на экран с явлением после­свечения, или произвести последовательное экспонирование зерен на фотопластинку с помощью пучка света, касательного к поверх­ности круга. Поскольку вершины зерен до определенной глубины не перекрываются, на экране можно определить количество и разно — высотность вершин зерен и установить закон их распределения по ширине и высоте слоя. Разновидностью метода является определение разновысотности вершин зерен поворачиваемого круга с помощью микроскопа [72].

Недостатки этих методов: невысокая степень разрешения раз­новысотности вершин в первом случае; большая трудоемкость, невозможность охватить всю поверхность круга и отсутствие фик­сации проекции зерен на бумаге — во втором.

Нами разработана методика [12], основанная на фиксации формы неровностей, оставляемых неперекрытыми вершинами зерен на поверхности плоского полированного клина, вращающимся с рабочей скоростью абразивным кругом. Измерения производятся в следующем порядке. Абразивный инструмент, например алмазный правящий ролик, импрегнированный порошками природных или синтетических алмазов, устанавливается на шпиндель продольно­шлифовального станка с биением, не превышающим 0,01 мм, и приводится во вращение с рабочей скоростью. Плоский клин, из­готовленный из материала, на котором при шлифовании образуются царапины без существенных искажений, имеющий малый угол наклона (1 : 250—1 : 400), устанавливается на магнитный стол станка.

Вручную, медленно стол перемещается в горизонтальной плос­кости до врезания ролика в клин на некоторую глубину ht (рис. 22), обеспечивающую полное слияние отдельных царапин. Зерна ро­лика, расположенные в наружном слое, прийдут в соприкосновение с клином в разных точках в соответствии с разновысотностью рас­положения. При соотношении сторон клина, например 1 : 400,

1 мм продольного смещения клина соответствует разновысотности, равной 2,5 мкм. Измеряя смещение царапин на клине с точностью до 0,2 мм, удается разделить зерна с разновысотностью в доли мик­рометра.

В качестве начала отсчета принимается царапина наиболее выступающего зерна. Ширина каждой царапины и число царапин по мере роста глубины врезания увеличиваются, и на некоторой глубине царапины сливаются в результате взаимного перекрытия (сечение 4—4).

Глубина перекрытия ht = hn характеризует момент, с которого начинается снятие материала по всей поверхности клина. В последу­ющих сечениях (от 5—5 до 9—9) профиль царапин остается неизмен­

Рис. 23. Схема последовательного формирования групповых царапин в сечениях

плоского клина.

(рис. 23, а, б). В сечениях 1—1 и 2—2, которые несут в себе проек­ции всех зерен круга на данном уровне врезания, наблюдаются лишь следы от отдельных наиболее выступающих вершин зерен, кинема­тически не перекрываемых друг другом. Эти сечения показаны в виде отдельных царапин, форма которых подобна форме сечения вершины зерна в плоскости, перпендикулярной к вектору скорости резания. Однако уже в сечениях 2—2, 3—3 и 4—4 (см. рис. 22) происходит все увеличивающееся наложение вершин зерен друг на друга, в результате царапина несет следы их коллективного воздействия и по ее форме уже невозможно определить форму вершин отдельных зерен. Это более наглядно показано после полного перекрытия цара­пин в сечении 5—5 (рис. 23, в, г). Здесь, например, царапина / образована зернами 13, 3,7 и 20, а царапина III — зернами 18, 5, 1,
16. Таким образом, чтобы определить эти зерна по интегральной форме царапины (/—II—III—IV и т. д.), необходимо на каждой из них найти следы от их вершин. Эти следы находятся достаточно просто по изменению кривизны и направления хода кривой на уча­стках наложения вершин друг на друга. На рис. 23, д показано начальное и конечное положение профилей неровностей после сня­тия припуска глубиной /ср, определяемого как расстояние между штрих-пунктирными линиями, являющимися средними линиями

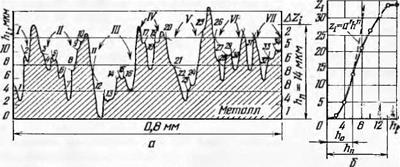
Рис. 24. Профилограмма неровностей на клине, прошлифованном алмазным правящим роликом зернистостью АСК 200/160 (а) и график распределения вершин зерен по глубине алмазного слоя (б).

шероховатости поверхности. Рассматривая нижний (заштрихован­ный) профиль неровностей, устанавливаем, что расчетная глубина резания hplT и фактическая глубина врезания зерен в материал не совпадают. Последняя больше первой на величину hn/2, т. е. на величину половины глубины царапин. Указанное несоответствие имеет важное значение, так как на графике силы резания в функции от изменения продольной и поперечной подач, определяющих ве­личину /ср, пройдут через начало координат и отсекут на оси сил отрезок, численно равный силам, возникающим на вершинах зерна при врезании на глубину hn/2 (см. работу [12]).

На рис. 24 приведена профилограмма неровностей на клине в сечениях после перекрытия царапин, образованных алмазным гальваническим роликом диаметром 60 мм, оснащенным синтетиче­скими алмазами марки АСК зернистостью 200/160. Профилограмма записана с помощью профилометра завода «Калибр» алмазной иглой с радиусом при вершине 0,01 мм при вертикальном увеличе­нии 4000 : 1 и горизонтальном увеличении 200 : 1. Как следует из профилограммы, на базе 0,8 мм располагается семь коллектив­ных царапин, образованных тремя (царапины /, IV, VII) и более вершинами (например, царапины II и III образованы соответствен­но вершинами зерен 8 и 6).

Справа от профилограммы показан график распределения вер­шин зерен по глубине царапин на величину 14 мкм. Установлено, что вначале до глубины h0 = 6 мкм распределение зерен следует некоторой монотонной кривой, отражающей нарастание плотности зерен по глубине ПС, а затем постепенно отстает от нее в связи со все большей степенью перекрытия вершин зерен друг другом. На­чало этого процесса показано на рис. 23, б, на котором в сечении 2—2 вершина зерна 4 перекрыта вершиной зерна 2. При этом зерно 4, находящееся впереди зерна 2, при совершении оборота круга прорезало канавку, которая затем была перекрыта и углублена зерном 2.

Следовательно, в процессе прорезания царапин перекрытыми зернами они не обнаруживаются нами, так как являются промежу­точными и не остаются на исследуемой поверхности. Этих царапин может и не быть вовсе, когда, например, зерно 4 следует при движе­нии за зерном 2. Степень перекрытия таких зерен увеличивается с глубиной слоя, и количество не обнаруженных зерен возрастает. После исчерпания глубины hn исчезают все зерна, так как канавки, прорезанные ими, были полностью перекрыты вышележащими зер­нами и обнаружить их существование по оставшимся следам обра­ботки не удается.

Таким образом, имеется слой зерен, лежащий на глубине h0, в котором зерна расположены по параболическому закону. Этот слой невелик, в связи с чем необходима достаточная база и высокая степень точности измерений разновысотности вершин зерен, чтобы быть уверенным в достоверности полученного результата. В связи с этим обращалось внимание на точность изготовления угла клина, плоскостность его опорной и клиновой поверхностей, жест­кость самого клина и хорошую прилегаемость к поверхности стола. Профилограммы записывались на достаточно большой базе (3—5 мм и более) так, чтобы было зафиксировано несколько десятков и сотен зерен. Степень увеличения профилограмм принималась высокой (более 1000 : 1 по вертикали), такой, чтобы можно было без затруд­нений различать следы вершин зерен.

Для отделения зерен, имеющих при вершине несколько высту­пов, которые могут быть принятыми за вершины разных зерен, проводился анализ нескольких сечений 1—/; 2—2; 3—3 и т. д. В каждом сечении записывалась профилограмма и создание так на­зываемого эффекта разновременности образования коллективной царапины. Если процесс образования царапин провести медленно вращающимся кругом при относительно высокой скорости продоль­ной подачи, например при подаче 1 мм на оборот круга, то в случае, когда царапина образуется одной криволинейной вершиной, про­филь будет образовываться одновременно во всех сечениях; если профиль коллективный, то он образуется в разных сечениях, т. е. неодновременно.

Анализ количества таких «сомнительных» зерен показал, что их доля не превышает 5—10% и в большинстве случаев этсй по­грешностью можно пренебречь. С учетом изложенного удалось стабильно получать надежные результаты по определению функции Z — f (hi) на участке 0 — h0 и экстраполировать функцию на
смежные с ним глубины, соответствующие фактической глубине внедрения зерен в обрабатываемый материал.

В тех случаях, когда методика измерений предусматривала оценку лишь числа зерен, а не соответствие формы царапины форме вершин зерен, нами использовались клинья, изготовленные из углеродистой стали, хорошо отполированные и оксидированные по рабочим поверхностям для получения нужного контраста между ца­рапинами и необработанной поверхностью. Кроме того, использова­лись клинья из стекла, ке­рамики, ситаллов, мрамора, | абразивов и других мате — риалов.

Отметим одно важное ^ требование к абразивному инструменту, у которого определяется закон распре — 40 деления зерен в слое: сте­пень притупления вершин 20 должна отсутствовать или быть меньше величины h0.

Этому требованию отвеча­ли алмазные инструменты и в первую очередь правя­щие ролики, оснащенные порошками синтетических или природных алмазов, а также абразивные круги сразу же после правки их правящими инструментами.

На рис. 25 представле­ны результаты измерения числа царапин, характери­зующих расположение вер­шин зерен 8 правящих роли­ков, изготовленных из порошков природных алмазов зернистостью от 250/200 до 1000/800 и концентрацией от 100 до 350%. Ролики имели размер 70 X 10 X 40 и были изготовлены методом спекания на металлической связке МП-2, имеющей высокие свойства по алмазоудержанию *.

Ролики перед измерением царапин прошли стадию вскрытия, устранения биений шлифованием кругом КЗ и имели небольшую степень приработки вершин. Из рис. 25 следует, что кривые Z£ = = f {hi) располагаются не в том порядке, который вытекает из плотности распределения зерен в матрице, задаваемой как размера­ми, так и концентрацией зерен. Они располагаются в соответствии с фактическим расположением вершин зерен, определяемым износом,

притуплением их и кинематикой движения. В результате этого у роликов, оснащенных алмазами 315/250 концентрацией 350 и 100%, 400/350 концентрацией 150%, а также 800/630 концентрацией 350 и 100%, произошло смещение всей кривой по отношению к началу координат влево. При этом кривые переплелись так, что, например, кривая рассматриваемой зависимости для ролика зернистостью 630/500 концентрацией 200% оказалась левее кривой ролика зер­нистостью 400/315. Аналогичным образом «незаконное» положение занимает кривая ролика зернистостью 315/200 концентрацией 350% и т. д.

Несмотря на то что в опытах принимались все меры, чтобы биение роликов было минимальным и одинаковым по величине, этого до­биться не удалось, хотя бы потому, что по наружной поверхности абразивного слоя невозможно точно замерить величину биений. Если добавить к этому ошибки в сочленении оправка — ролик и при постановке оправки на шпиндель станка, то станет ясным, что полу­ченные кривые не должны занимать тот строгий порядок, который следовал бы из строения слоя в статической модели инструмента.

Таким образом, для решения практических задач не следует при­менять статическую модель. При этом из-за невозможности учесть заранее влияние всех факторов при переходе от этой модели к вра­щающемуся кругу, т. е. к кинематической модели, не будет полу­чена требуемая практическая точность.

Несомненным является то, что предлагаемая методика с доста­точной для практики точностью позволяет определить фактическое распределение вершин зерен во вращающемся инструменте и отра­жает рабочее состояние слоя и влияние на нее системы СПИД в ки­нематике ее движения. Совершенно очевидно, что полученные на рис. 25 кривые до глубины /і<, не являются строго квадратичной пара­болой. Для выяснения характера этих кривых была произведена аппроксимация координат экспериментально найденных точек урав­нением прямой и кривыми различных порядков. Относительные и абсолютные ошибки такой замены представлены в табл. 8.

Для этой цели использовались методы аппроксимации точек различными уравнениями вида е“х ь, ахп, ах? + bx2 + сх + d, ах2 — Ь Ьх + с по методу наименьших квадратов на ЭВМ «Наири» и в > отдельных случаях на электронном калькуляторе РС-1001 фирмы «Шарп». Точность замены оценивалась абсолютной е и относитель­ной ф ошибками, вычисленными по известным зависимостям

где Цф — экспериментальные координаты точек; yv — вычисленные координаты точек; п — количество точек.

Из табл. 8 следует, что экспериментальные данные лучше всего аппроксимируются уравнением квадратичной параболы, хотя в

Таблица В Оценка точности аппроксимации экспериментальных точек рис. 25 уравнениями Зернистость и концентрация алмазов Исходные уравнения 250/200, 100% 315/250, 350% 315/250, 100% 400/315. 150% € Ф в ф e Ф e Ф ах2 + Ьх + с 2,6 18 3,0 6 1,2 6 1,4 8 ахп + с 1.7 11 3,8 9 2,4 11 1,6 11 евх+с 14,7 37 7,4 18 2,2 10 1,3 7 ах3 + Ьх2 + сх — f — d 2,8 9 — — 1,2 5 U 9 kx — f — b 3,7 9 3,0 6 1,9 9 2,8 16

Продолжение табл. 8 Зернистость и концентрация алмазов Исходные уравнения 630/500. 200% 800/630, 350% 800/630, 100% 1000/800, 250% е Ф е Ф е Ф е Ф ах2 + Ьх + с 0,5 3 1,3 5 1,0 8 0,5 4 схп + с 1,5 13 0,9 4 1,4 7 0,7 6 еах+с 4,1 17 7,4 18 3,7 18 1,7 14 ах3 + Ьх2 + сх + d 0,9 4 — 1,1 24 2,1 15 kx-}- b 1,4 6 4,4 21 1.7 9 1,2 10

отдельных случаях с ошибкой ф = 5 — г — 10% применимы и другие зависимости, в том числе уравнение прямой.

Заслуживает также внимания возможность экстраполяции экс­периментальных данных уравнением у = ахп, простым в графи­ческой обработке, с использованием двойной логарифмической сетки.

В табл. 9 показано изменение величины коэффициентов а, Ь, с в уравнении параболы у = ах2 + Ьх + с в связи с изменением числа точек, принимаемых при аппроксимации. Существенное их колеба­ние связано с тем, что рассеивание ординат экспериментальных данных вблизи абсциссы h0, связанное с ошибками измерения и дис­персией рассеивания размеров зерен и расположения их вершин, а также с явлением экранирования зерен, значительно влияет на расположение аппроксимирующей кривой при ограниченном числе точек. При этом относительная точность аппроксимации от числа использованных точек может существенно не изменяться. Так, например, для ролика, оснащенного алмазами зернистостью 630/500, концентрацией 200% при аппроксимации уравнения по 11, 12 и 13 точкам все три результата находятся в 10%-ной зоне ошибок,

Значения параметров уравнения у = ах3 + Ъх + с и величин й0 и Лп Зерннс- тость и кон­центрация алмазов п1 а ft С х„ Ч9 е Ф.% Ад, МКМ Лп, МКМ Уравнения типа ахп+Ь 250/200, 6 0,20 1,16 —5,3 -2,9 —7,0 2,6 18 12 21 0,037Л?’85 100% 8 0,08 2,70 -9,0 -16,5 —256,0 4,0 17 — — 315/250, 350% 8 0,25 8,77 -0,1 — 8,8 3,0 6 9 10 l,65ft{’91 + 12 315/250, 6 0,24 0,04 11.1 -0,1 -11,1 2,8 11 12 17 1,21Л)(3б + 8 100% 8 0,04 2,84 4,4 —35,5 -119,8 1.2 6 — 400/315, 11 0,07 -0,23 -3,7 -1,7 3,5 1,4 8 23 27 0,12ft,1,77 + 2 150% 13 0,01 1.14 -1.0 -57,0 0,9 3,4 9 — 630/500, 11 0,06 0,53 —0,3 -4,3 —8,8 0,5 3 22 29 0.11Л}-97 + 1 200% 12 0,04 0,88 —0,9 -1,5 -5,9 0.9 5 13 0,03 1.14 -1.9 —17,8 —12,1 1,4 6 — — 800/630, 12 0.08 0,05 3,4 —0,3 -3,4 1,2 5 0,057ft?’15 + 4 350% 13 0,09 0,01 3,3 —0,5 3,3 1,3 5 25 29 800/630, 10 0,04 0,60 -1.3 -7,0 -3,3 1,0 8 20 29 0,045ft7,15 100% 11 0,03 0,81 -2,0 —12,8 -7,1 1,1 8 14 0,02 0,99 -2,0 —24,8 -2,0 1.1 5 — — 1000/800, 350% 11 0,04 0,14 0,2 -1,8 0,8 0,5 4 22 25 0,045ft|-95

однако за истинное положение параболы следует принять то, при котором значение а будет наибольшим при минимальных значениях Ъ и с, что обусловливает наилучшее совпадение условного начала координат с расчетным (действительным, но утраченным в силу износа, например, вершин зерен или по другим причинам). При этом относительное смещение действительного и условного начала коор­динат, характеризуемого величинами х0; у0, минимально.

На основании проведенного анализа можно сделать вывод, что точка 11 еще принадлежит искомой параболе, а 12-я и 13-я точки (табл. 9) лежат уже на искаженной явлением экранирования зерен части кривой (рис. 25) Очевидно, что в качестве рабочей части пара­болы следует взять точки от вычисленного начала координат х0 = = —4,3 мкм до точки h0 = 22 мкм, т. е. глубины слоя, равного 26,3 мкм, и рассчитать число вершин зерен по уравнению z£ = = 0,06 hh. Здесь hpi включает отрезок х0 и координату глубины, отсчи­танную от вершины наиболее выступающего зерна ролика. Зерна, определенные в интервале до точки h0, не перекрываются и поэтому все соприкасаются с обрабатываемым материалом, снимая с него стружку или образуя канавку без удаления обрабатываемого мате­риала. С этой точки зрения все эти зерна являются режущими. После точки Л0 часть зерен экранируется, поэтому общее число зе­рен, находящихся в рабочем слое на глубине hpi > h0, по-прежнему вычисляется по приведенному уравнению, экстраполированному на большие, чем это определено экспериментом, глубины.

Таким образом, экспериментально установлено, что при отно­сительно небольшой степени износа вершин зерен и колебаний аб­разивного слоя по отношению к поверхности вращения шлифоваль­ного круга количество зерен в рабочем слое может быть определено по числу и глубине царапин и аппроксимировано уравнением параболы. В тех случаях, когда простота обработки эксперимен­тальных данных играет важную роль или когда аппроксимация параболической кривой не приносит выигрыша, следует исполь­зовать уравнение вида Z{ = ah’), параметры которого просто опре­деляются по экспериментальным точкам, аппроксимированным прямой в двойной логарифмической сетке (см. табл. 8).

Поскольку полученные уравнения параболического вида экс­траполируются на большие глубины, по сравнению с глубинами, на которых были определены царапины, то ошибка вычислений возрастает с увеличением глубины изучаемого слоя. Поэтому не­правомерно использовать их для вычисления числа зерен на всей глубине слоя, соизмеримой с размерами самих зерен.

Установив экспериментально-расчетным путем распределение вершин зерен по глубине рабочего слоя, можно перейти к решению следующей задачи — выяснению кинематики взаимодействия этих зерен с обрабатываемым телом.

1. Кинематика взаимодействия шлифовального круга с обрабатываемым телом

Выделение контактирующих зерен. Для рассмотрения кинема­тической задачи остановимся на методе врезного шлифования, ко­торый, на первый взгляд, отличается большей простотой движений, чем методы наружного и внутреннего шлифования с помощью про­дольных проходов круга. В рассматриваемом примере имеются три технологических движения: вращение детали со скоростью нд, вращение круга со скоростью vKp и взаимное сближение центров вращения детали и круга в поперечном направлении со скорос­тью 5М.

Скорость сближения центров вращения 5М не будем отождеств­лять с величиной поперечной подачи, чтобы не путать в дальней­шем, как это нередко бывает, величину 5М : пкр = Soe с глубиной шлифования tpc3 (где пкр — число оборотов шлифовального круга, мин; Sоб — величина перемещения рассматриваемых центров за вре­мя одного оборота шлифовального круга, мм/об).

Поскольку термин «поперечная подача» прочно вошел в техни­ческую литературу, то в дальнейшем величина Sоб будет наимено — ваться по установившейся традиции подачей на 1 оборот круга.

Как только вращающиеся объекты — круг и деталь — прийдут в соприкосновение и каждая вершина зерна получит свою траекто­рию движения, вступит в силу явление экранирования зерен; зерна разделятся на две группы — контактирующие или режущие, совершающие работу деформации обрабатываемого материала, и перекрытые, не имеющие в рассматриваемый момент времени кон­такта с деталью.

Контактирующие зерна в свою очередь подразделяются на зер­на, удаляющие обрабатываемый материал с поверхности детали в виде стружки, и на зерна, перемещающие пластически материал из объема канавки на ее боковые стороны.

Для анализа более правильно режущими зернами называть все зерна, на которых возникают усилия и выделяется тепло в результате пластического или хрупкого разрушения материала детали, а не только те, которые образуют стружку. Это тем более важно, что число стружкоотделяющих зерен, строго говоря, ко­личественно менее определенно, чем число контактирующих. Оче­видно, с точки зрения энергетических затрат, анализа тепловых потоков, износостойкости шлифовального инструмента и дефектных слоев на обработанной поверхности необходимо знать именно число контактирующих зерен.

Отметим, что как число зерен, снимающих стружку, так и число контактирующих зерен во времени непостоянно и может рассматриваться как случайная величина, рассеянная около сред­него значения.

В результате того, что обрабатываемый материал, вытеснен­ный из образованной канавки в виде валиков, почти в 1,5—2 раза увеличивает глубину срезаемого последующими зернами слоя, изменяется число контактирующих зерен (в работу вступят вер­шины, ранее «не достававшие» до обрабатываемого материала), и, кроме того, при большей глубине создаются лучшие условия отделения стружки для ранее «пропахивающих» зерен и они пере­ходят в число зерен, отделяющих стружку. При срезании таких валиков число последующих контактирующих и снимающих струж­ку зерен в данном месте контакта уменьшается до момента образо­вания новых валиков, приводящих вновь к росту работающих зерен.

Необходимо отметить, что по мере износа абразивного слоя шлифовального круга ранее экранированные зерна выходят на на­ружную поверхность и вступают в контакт с обрабатываемой поверхностью. Таким образом, в абразивном круге в этом смысле нет неработающих, т. е. не совершающих работу по деформированию обрабатываемого материала, зерен.

Поскольку одни и те же зерна могут в разные моменты времени быть как стружкоснимающими, так и пропахивающими, то весьма затруднительно выделить их из числа контактирующих. В большин­стве случаев этого и не требуется. Достаточно сравнить произво­дительность шлифования, выражаемую в количестве снятого ма­териала (г, см2) в единицу времени для двух условий обработки {режимов или двух сравниваемых абразивных кругов), характери­зуемых равным количеством зерен, находящихся на равной площади контакта, чтобы оценить относительное влияние числа «полезно» работающих зерен в общем количестве зерен, участвующих в про­цессе шлифования.

Таким образом, в дальнейшем будем понимать под режущими зернами все зерна, участвующие в непосредственном взаимодействии с обрабатываемым материалом.

В связи с параболическим законом распределения и явлением экранирования число режущих зерен ПС ограничено, составляет несколько процентов числа зерен в слое матрицы сопоставляемой глубины, а число мгновенно контактирующих зерен, как это будет ясно из дальнейшего, исчисляется всего несколькими десятками штук, а в отдельных случаях — единицами.

Наряду с ПС выделим в инструменте рабочий слой (PC). Под PC следует понимать пространство над связкой инструмента, в которой размещены выступающие вершины зерен. В этом слое целесообразно дополнительно выделить рабочий поверхностный слой (РПС), вершины зерен в котором непосредственно заглуб­ляются в обрабатываемый материал В PC инструмента совершает­ся основная работа по шлифованию, отделяется обрабатываемый материал и размещаются продукты его диспергирования, образую­щийся шлам (остатки абразивных зерен и связки), а также сма­зочно-охлаждающая среда. В связи с этим для нормальной работы шлифования должно осуществляться неравенство РПС < PC, т. е. глубина врезания зерен РПС должна быть всегда меньше

глубины выступания зерен под связкой. Таким образом, имеем соподчинение слоев: РПС < PC < ПС.

Для практических расчетов можно не рассматривать весь ПС, вполне достаточно располагать данными о распределении числа ре­жущих зерен на участке кривых Obkt и 0/г2 (см. рис. 21) В преды­дущем разделе показана возможность определения числа и характера распределения зерен на этих участках на основании анализа цара­пин, оставляемых кругом на поверхности обработки при врезном шли­фовании (как было показано, врезание лучше осуществлять на плос­ком клине или плоской поверхности с малой продольной подачей).

Если известна кривая распределения общего количества зерен в РПС инструмента, которая лучше всего аппроксимируется урав­нениями типа у = ах2 + Ьх + с или у = axj + b, то число контак­тирующих зерен с достаточной для практики точностью может быть определено с помощью касательной к этой кривой в точке h0, т. е. в точке, соответствующей глубине, с которой начинается экраниро­вание зерен (в точке исчезновения первого зерна). Обоснование это­го метода выделения дано в работе [12] и дополнительно будет рас­смотрено ниже.

Число контактирующих зерен определяется в зависимости от вида аппроксимирующего уравнения (примем, что у = Z, х = Л£): от начала координат до глубины /г0

= ahi + bh0 + c или ZK = ahl + b (2.1)

от глубины h0 до глубины ht = tpe3 zi = ZK + (2aho + b) (hi — h0); Zt = ZK + nah?~’ (h, — h0). (2.2)

В выражении (2.2) второе слагаемое представляет уравнение

dZ

касательной с угловыми коэффициентами — щ- «= 2ah0 + Ь или dZ Л. л—і dhi ~ /(! ‘

Кинематика врезной правки абразивного круга. Для уяснения принципа расчета траекторий движения зерен, формы стружки и площади контакта рассмотрим процесс правки абразивных кругов правящими роликами, оснащенными алмазами.

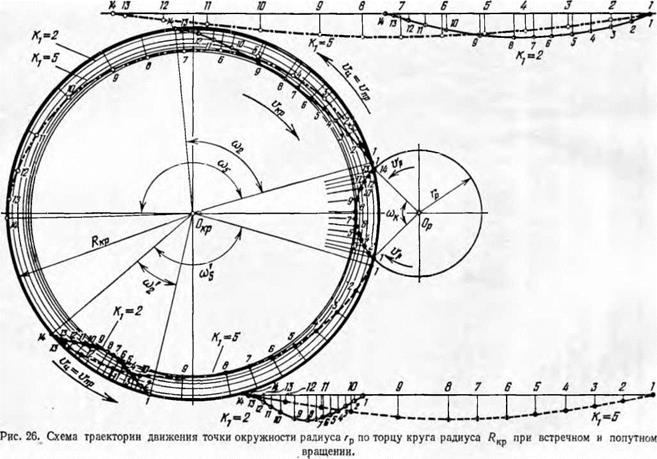
С этой целью проделаем некоторые графические построения. На рис. 26 показаны траектории движения избранных точек правя­щего алмазного ролика радиусом гр с центром вращения Ор по отношению к торцовой плоскости абразивного круга радиуса RKp с центром вращения Окр. Схема фиксирует произвольное проме­жуточное положение расстояния между центрами 0кр — Ор, когда торец ролика наложился на торец абразивного круга на некоторую величину Д = (Дкр + гр) — ОкрОр. В этом положении для простоты дальнейших построений сближение центров приоста­новлено (SM = 0), а круг и ролик приведены во встречное или по-

1Л_

путное вращение с различным соотношением скоростей: Ki = —— = = 2иК1 = 5. Г’Р

Соотношение диаметров вращающихся тел К3 = р « 3. Па-

“р

раметры Ki и /(я определяют однозначно и соотношение чисел обо­ротов, так как

*г=И =т*

В нашем примере соотношение чисел оборотов абразивного круга и правящего ролика принято меньшим и большим единицы, при этом Кч = 2/я и 5/3.

Разбив последовательно дугу ролика с центральным углом tuK, точки которой соприкасаются с кругом, на 13 отрезков (причем пары точек 1—14, 2—13, 3—12, 4—11, 5—10, 6—9, 7—8 находятся на одной окружности), легко найти графически траектории движения этих точек по плоскости торца круга при встречном движении (изображено в верхней половине круга) и при попутном движении (изображено на нижней половине рисунка) точки 1 и 14.

Формы траектории движения точки 1 по отношению к наружной окружности круга при встречном и точки 14 при попутном вращении более наглядно показаны на развертке окружности в линию от­дельно в верхней и нижней части рисунка.

Устанавливаем, что при А = const длина траектории движения избранной точки правящего ролика существенно зависит от направ­ления движения и соотношения скоростей вращения ролика и круга.

При встречном вращении и при /Сх = 5 длина траектории на плоскости круга наибольшая, при попутном вращении и при К = = 2 длина траектории наименьшая. Определим соотношение длин изображенных четырех траекторий, выраженных через длину на­ружной окружности круга.

В любом случае длина пути /тр = ипрт, где /тр — длина траекто­рии; vnp = иКр ± vр — скорость правки, т. е. скорость относитель­ного движения круга и ролика; т — время контакта точки 1 (или 14) с торцом круга. Для принятых условий время контакта при ир = const и A = const постоянно. Имеем

икр2 ± VP ’

Здесь /ТР1 — длина траектории движения точки при скорости вращения круга икрі; /тр? — длина траектории при скорости вра­щения круга иКр2‘. К[ и Кі — соотношения скоростей круга и ролика при скорости круга икрі и икр2.

Для рассматриваемого примера при К = 5 и К = 2 имеем соотношение длины траекторий при встречном вращении: /тРі :

: ^тр2 = (5 + 1) : (2+1) = 2; при попутном вращении /ТР1 i lTPt =

= (5 — І) : (2 — 1) = 4.

Из формулы (2.3) устанавливаем, что соотношение длин траек­торий определяется не абсолютными значениями скоростей, а ве­личиной Кх, а при выбранных их размерах (К* = const) — соот­ношением чисел оборотов вращающихся тел и направлением вза­имного вращения (равном 1 при встречном и —1 при попутном движении).

Рассмотренный пример дает нам право при кинематическом анализе перейти от многообразия значений скоростей движения, размеров шлифовальных инструментов, деталей и чисел оборотов к их соотношениям Ki, К2 и Ка — Таким образом, существенно со­кращается число переменных, а кинематика движения вершин зерен шлифовальных инструментов может быть сведена к функции трех К.

Отметим также, что величина прогиба — расстояния текущей точки траектории движения от внешней (начальной) окружности круга — переменна по длине и описывается практически равно­бокой кривой, плавно сопрягающейся в точках «входа» и «выхода» с окружностью круга.

Очевидно, нет необходимости отыскивать уравнение указанной кривой в функции от значений Кг; К2 К3 и находить, например, сред­нее значение отклонения кривой от окружности. Это привело бы к неоправданным усложнениям расчетов.

Для анализа вполне достаточно оперировать длиной траекто­рии движения, спроектированной на избранную окружность кру­га, т. е. дуговым расстоянием между точками входа и выхода траектории на наружную поверхность обрабатываемого тела, и оперировать значением Д — величиной сближения центров вращаю­щихся тел за рассматриваемый промежуток времени, например за время одного оборота круга (обрабатываемой детали) или ролика (шлифующего инструмента).

При построении картины взаимодействия правящего ролика и шлифуемого им тела (абразивного круга) ради простоты построе­ний была нарушена действительная картина кинематического вза­имодействия рассматриваемой пары. В самом деле, вместо постепен­ного сближения центров 0Кр и 0р, был выхвачен момент, соответ­ствующий внедрению ролика в круг на величину Д, а затем сближение центров было приостановлено. Таким образом, не была выяснена предыстория сближения круга и ролика от момента начального соприкосновения до внедрения на величину Д, а так­же последовательность нанесения царапин и их слияния при про — . должающемся сближении центров 0кр и Ор.

Указанный пробел восполнен на рис. 27 и 28. На первом показа­на схема резания и стружкообразования при значениях Ki *= 5,2; К2 = 1.04; К3 = 5 для четырех вершин зерен, симметрично распо­ложенных на внешней окружности ролика с диаметром dp. На втором

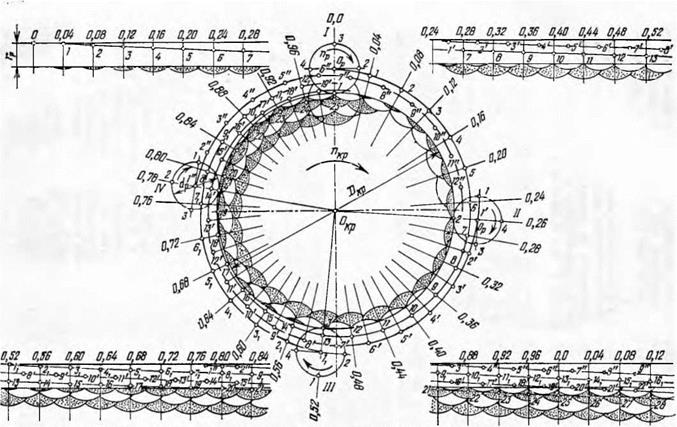
Рис. 27. Схема нанесения царапин на поверхность абразивного круга зернами правящего ролика при встречном вращении при К~= 1,04 (арабские цифры без штрихов — положение центров ролика по отношению к абразивному кругу при контакте с по­верхностью круга зерна 1, с одним штрихом — то же для зерна 2, с двумя штрихами — для зерна 4 и с индексом 1 — для зерна 3).

показана аналогичная схема при Л, = 6; К3 — 5 и К2 = 1,2 Величины К по абсолютным значениям в этих двух примерах при­няты одинаковыми (например, K:i) или несущественно разнятся. Однако схемы нанесения царапин на круг отличаются принципиаль­но, и решающим фактором здесь является изменение величины К2-

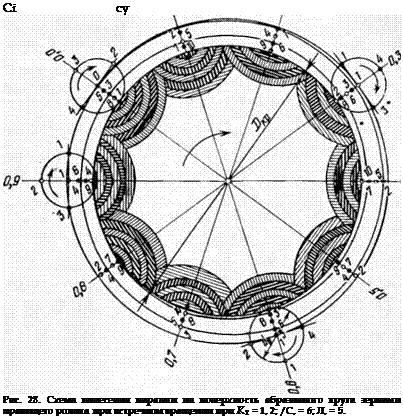Поясним это при рассмотрении очередности нанесения царапин на. поверхности круга.

При К2 = пкр/пр = 1,04 на каждый оборот шлифующего ин­струмента (правящего ролика) обрабатываемая деталь (абразивный круг, подвергающийся правке) повернется на 1,04 оборота. При втором обороте ролика круг сделает 1,04 X 2 = 2,08 оборота, при третьем 1,04 X 3 = 3,12 оборота и т. д. Тогда траектории движения наиболее выступающей точки вершины зерна, например 1, будут располагаться на шлифуемой поверхности со строгой зако­номерностью по отношению к исходной точке отсчета — нулевой точке, образуемой в месте начального касания зерна 1 поверхности круга при сближении центров Окр и Ор. Выразим шаг между средними

і О —0.04		23 24 25 26 и т. д. —0,90 —0.94 —0,0 —0,04 и т. д.

 

Вверху ряда проставлен порядковый номер оборота ролика, внизу — соответствующее месторасположение центра царапины на цилиндрической поверхности круга. Устанавливаем следующие за­кономерности:

1. Расстояния между центральными точками царапин при рав­номерном вращении ролика и круга равны между собой и состав­ляют 0,04 длины окружности, т. е. /м. ц = 0,04лПкр.

2. Величина относительного шага между центрами царапин Ш определяется величиной К2, т. е. передаточным отношением /і„р : п. Величина шага определяется дробным остатком величины Д9, т. е. Ш = (1,04—1) = 0,04.

3. Число царапин при известном Ш рассчитывается как отноше­ние 1 : Ш. Таким образом, число царапин, нанесенных на всю поверхность круга, составит в нашем примере 1 : 0,04 = 25, после чего цикл повторится, поскольку делимое целое число — 26-я царапина наложится на первую, 27-я — на вторую и т. д.

4. Поскольку на каждый оборот ролика при скорости врезания SM мм/мин центры вращения пары ролик — круг сблизятся на величину Д = SM/np, то после цикла в 25 оборотов ролика ради­альное расстояние между наибольшей глубиной, например 20-й

С

царапины и 45-й царапины, будет равно 25Д = 25 -~ = 255об,

"р

где Sоб — поперечная подача, рассчитанная на 1 оборот шлифую­щего инструмента.

5. В связи с увеличением глубины врезания одной и той же точки ролика с каждым оборотом ролика на величину Д = глубина, ширина и длина последовательно образуемых 1-й, 2-й, 3-й и т. д. царапин непрерывно возрастают. В результате наступает такой момент, когда при определенной величине сближения центров Ор и Окр длина царапин /и станет равной расстоянию между цент­рами царапин, т. е. /ц = /м. ц = ШяПкр и в дальнейшем перестанет возрастать, т. е. стабилизируется. Аналогично при определенной в общем случае иной глубине внедрения шлифующего инструмента в поверхность круга произойдет слияние царапин по ширине и ста­тистически не только длина, но и ширина среза стабилизируются. С этого момента не останется ни одного участка поверхности круга, не покрытого царапинами — образуется новая обработанная по­верхность. Цикл предварительного врезания закончится, начнется сам процесс шлифования, характеризуемый определенным постоян­ством параметров глубины, ширины, длины среза, приходящихся в среднем на отдельно взятое зерно.

6. Последовательно образуемые царапины касаются общей ли­нии — архимедовой спирали (образуемой в результате сочетания равномерного вращения круга и радиального смещения самих цара­пин) с шагом, равным 25 Зоб-

7. Кинематика образования царапин на поверхности круга в результате взаимодействия отдельных зерен с обрабатываемым те­лом наиболее близка к схеме, известной в практике резания как схема точения «летучими» резцами.

На рис. 27 показана последовательность образования царапин для зерна I и смежных с ним зерен 2, 3 и 4. Схема движения всех точек совершенно идентична, только начальные точки отсчета цара­пин по отношению к зерну 1 смещены на величину запаздывания, соответствующую их местоположению на окружности круга.

Покажем положение нулевой точки, т. е. точки первого касания зерна 1, и положение середины 1-й царапины на поверхности круга для зерен 2, 3, 4 по отношению к этой точке:

зерно 1: 1,04 X 0 = О X лПкр зерно 2: 1,04 X V4 = 0,26лЦ<р зерно 3: 1,04 X 2/4 = 0,52лПкр зерно 4: 1,04 х 3/4 = 0,78лПкр

1.4 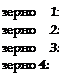х 1 = 1,04лДф

1.4 X и/4 = 1,30яЦф

1.4 х 12/4 = 1,56лDKp

1.4 X 13/4= 1,82яЦф

Таким образом, первые царапины, которые образуются на круге для зерна 1, при втором обороте (при первом была нулевая царапина— точка) будут расположены от начала отсчета на 0,04 доли окружнос­ти; для зерна 2 первая царапина расположена в точке, находящейся на 0,26 доли окружности, а для зерен 3 и 4 — соответственно в точках 0,52 и 0,78 доли окружности. Положение ролика в этих местах окружности круга отмечено на схеме окружностью с соот­ветствующим поворотом на V4; V, ; и 3/4 оборота. При этом зерна 2, 3 и 4 царапают круг на глубину соответственно V4; V2; 3/4 S0б- Для зерна I положение окружности зафиксировано в нулевой точ­ке, при этом глубина резания, естественно, равна нулю.

При втором и последующих оборотах ролика царапины для ка­ждого зерна начнут смещаться по отношению к предыдущей цара­пине на постоянную величину, равную шагу Ш = 0,04 доли окруж­ности. Распишем цикл их образования:

зерно 1: 0-0,04—0,08-0,12—0,16—0,20—0,24—0,28—

0, 32—0,36—0,40—0,44—0,48—0,52—0,56—0,60—0,64—

0,78—0,72—0,76—0,80—0,84—0,88—0,92—0,96—0—

0,04 ит. д.;

зерно 2: 0,26—0,30—0,34—0,38— 0,42—0,46—0,50— 0,54—0,58—0,62—0,66—0,70—0,74—0,78—0,82—0,86— 0,90—0,94—0,98—0,02—0,06—0,10—0,14—0,18—0,22— 0,26 и т. д.;

зерно 3: —(),.»2—0,56—0,60—0,64—0,68—0,72—0,76— 0,80—0,84 0,88—0,92—0,96—0—0,04—0,08—0,12—

0,16—0,20-0,24—0,28—0,32—0,36—0,40—0,44—0,48—

0,52 ит. д.;

зерно 4- —0,78—0,82—0,86—0,90—0,94—0,98—0,02— 0,06—0,10—0,14—0,18—0,22—0,26—0,30—0,34—0,38— 0,42—0,46—0,50—0,54—0,58—0,62—0,66—0,70—0,74—

0,78 и т. д.

Из анализа приведенного материала следует, что через некото­рое число оборотов ролика геометрическое расположение царапин на поверхности круга упорядочивается.

Если в начале врезания за первый оборот ролика возникали царапины (см. рис. 27) в точках круга /—II—III—IV (соответ­ственно в позиции 0—0,26—0,52—0,78), а затем с каждым оборотом ролика царапины последовательно смещались по часовой стрелке на величину шага 0,04, увеличивая свою глубину и длину, то после слияния (как показано на схеме на седьмом обороте ролика) длина царапин стабилизировалась и становилась равной /ц = 0,04лТ)кр. В дальнейшем царапины от разных зерен начинали накладываться друг на друга, при этом возникал момент, когда накопленная глу­бина врезания распределялась равномерно между зернами.

Проследим за этим моментом (см. рис. 27) на примере взаимо­действия зерен I и 2. Центры мгновенного вращения ролика в по­ложениях царапин 0,04—0,08—0,12… ит. д. обозначены арабскими цифрами /—2—3 … и т. д. и расположены на архимедовой спирали, смещающейся в зафиксированных точках к центру Окр на величину, равную S06- Через семь оборотов царапины достигнут места круга, соответствующего длине 0,28лД<р, т. е. минуют участок поверхности круга, на котором уже были образованы ранее царапины зерном 2 (напомним, что они начались на дуге, отстоящей от начальной точки отсчета на величину 0,26яОкр). Очевидно, с этого момента зерно 1 будет срезать меньшее количество материала на величину объема царапин, образованных зерном 2.

Уменьшение объема среза будет происходить до момента слияния царапины зерна 2 (этот момент по схеме соответствует положению центра вращения ролика в точке 12).

В дальнейшем объем материала, снимаемый зерном 1, стаби­лизируется, так как устанавливаются постоянными длина царапи­ны и ее глубина, что приводит к постоянству и ширины царапины.

Рассуждая аналогичным образом по отношению следующей пары зерен 2—3 3—4 и 4—1, устанавливаем, что и для них после 12 оборотов ролика согласно схеме наступит стабилизация объемов материала, снимаемого каждым зерном (см. развертки вверху и внизу рис. 27).

Таким образом, врезное шлифование разбивается на два этапа:

1. Этап предварительного врезания, во время которого зерна постепенно углубляются в обрабатываемый материал, в результате чего непрерывно увеличиваются длина, глубина и ширина царапины. Объем среза и, следовательно, усилие на каждом зерне непрерывно возрастают.

2. Этап стабилизации процесса, который характеризуется мо­ментом слияния царапин по окружности и ширине обрабатываемой детали. Начиная с этого момента устанавливается постоянный объем работы, совершаемый каждым зерном за время контакта с деталью.

Группировка царапин. При равенстве объемов материала, приходящихся кинематически на каждое отдельное зерно, может изменяться соотношение величин сечения и длины среза в связи с явлением так называемой группировки царапин.

Явление группировки царапин существенным образом влияет на продольную форму среза и заслуживает специального рассмо­трения. Оно зависит от комбинации положений начальных точек соприкосновения зерен с обрабатываемым телом. В свою очередь положение последних определяется численным значением К‘2 и закономерностью взаимного расположения самих зерен на окруж­ности шлифующего инструмента вдоль траектории вращения.

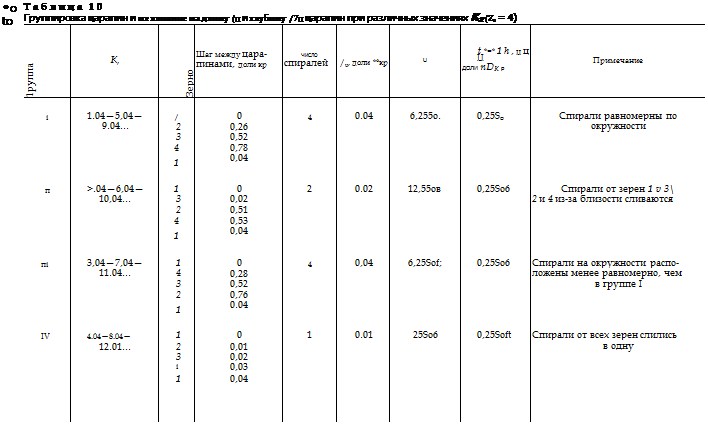
В табл. 10 показано положение начальных точек соприкосно­вения рассмотренных ранее симметрично расположенных в ролике четырех зерен с поверхностью круга, от которых начинается об­разование спирали Архимеда, касательной ко дну канавок цара­пин, в зависимости от изменения целой части передаточного отноше­ния К2.

Устанавливается, что передаточные отношения К2 при этом кинематически не равноценны и образуют четыре отдельные груп­пы, в которых точки развертки архимедовых спиралей занимают одинаковое положение. В группе I К2= 1,04—5,04—9,04 и т. д. начальные точки расположены равномерно по окружности: 0—0,26—0,52—0,78—0,4; в группе II К2 = 2,04 —6,04—10,04— щДш; ~оЗб о.2б 0І26

14,4 … начальные точки 0—0,51—0,02—0,53—0,04 …; в группе III

iuc=o.5i олП оГНЇ оГм

К2 = 3,04—7,04—11,04—15,04… начальные точки располагаются в порядке 0—0,76—0,52—0,28—0,04 …, что при перестановке зерен 2 и 4 местами равнозначно 0,0—0,28—0,52—0,76—0,04 …; в группе

(щЗш 0/24 ‘о24_ 028

IV К2 = 4,04—8,04—12,04—16,04… распределение точек после­довательное: 0—0,01—0,02—0,03—0,04. Здесь Шс — относительное Ш^ООі’_ООІ 0.01 о. оР

расстояние между начальными точками спиралей.

В этой группировке группы I, III практически равноценны, так как в них расстояния Шс между точками образования четырех ар­химедовых спиралей (царапины от каждого зерна образуют свою сяираль, а сами спирали практически равномерно расположены по окружности) близки по значениям. Наибольшая глубина между царапинами, равная радиальному расстоянию между ветвями

 

1,2—5,2—9,2	1 и 3	0*—0,2—0,4— 0.6—0,8
	2 и 4	0.1—0.3—0,5— 0.7—0,9
2,2—6,2—	1	0
10,2…	2	0,05
	3	0,10
	4	0,15
	1	0,20
3,2—7.2—11,2	1	0
	2	0,20
	3	0,40
	4	0,60
	1	0.80
4,2—8,2—12,2	1	0
	2	0,05
	3	0,10
	4	0,15
	1	0,20

0.1	2,55об	0,25So	Десятиугольная «звездочка» из двух пятиугольных, смещенных на 0,1 шага
0,05	5,0So6	0,25So6	Двадцатиугольная «звездочка» с шагом 0,05
0,20	1,255o5	0„25So’	Пятиугольная «звездочка» с ша­гом 0,2
0,05	5»0So6	0,25So5	Двадцатиугольная «звездочка» с шагом 0,05

архимедовых спиралей, в этих группах одинакова, поэтому в течение цикла (равного времени 25 оборотов ролика) зерна 1—2—3—4 срезают практически одинаковые срезы, работают с одинаковой глубиной резания, которую можно определить из отношения (0,25 : 0,04) = 6.25S,*.

В группе II начальные точки развертывания царапин (начало выхода архимедовых спиралей) распределены по окружности не­равномерно. Для зерна 1 это точка 0, для зерна 3—0,02, для зерна 2 — 0,51 и для зерна 4 — 0,53. При этом практически из-за совпа­дения расположения спиралей зерен / и 3, 2 и 4 резание будет осу­ществляться как бы по двум спиралям с глубиной (0,50 : 0,04) Sof = — 12,2550б.

В группе IV, в которой зерна за один оборот создают царапины в строгой последовательности с шагом 0,01, образуется одна спи­раль, так как такая очередность врезания зерен приводит к схеме резания одним зерном, но с шагом, в 4 раза меньшим (0,04 : 4 = = 0,01). После завершения цикла в 25 оборотов ролика глубина резания, т. е. радиальное расстояние между ветвями спирали, со­ставит 25S06 из расчета (1 : 0,04) So6 = 25S06-

Итак, устанавливаем, что группирование царапин, вызываемое в рассмотренном примере изменением целочисленной части парамет­ра К2, приводит к изменению максимальной глубины среза, опре­деляемой радиальным размером расстояния между ветвями одной или смежных архимедовых спиралей (проведенных касательно к дну царапин) и пропорциональным изменениям длин царапин таким образом, что во всех случаях объем среза, срезаемый каждым зер­ном, остается неизменным.

В самом деле, если в группах I и III образовалось четыре спира­ли и длина царапины равна /ц = 0,04я£)кр, а глубина Лц = = 6,25So6, то для группы II спиралей две. Расстояния между ветвями этих спиралей равны и составляют величину, в 2 раза боль­шую и равную 12,55об, а величина расстояний между царапинами, определяемая расстояниями между смежными начальными точками касания зерен с поверхностью круга (см. табл. 10), составляет 0,02— 0 = 0,02лІ)кр (зерна 3 и /) и 0,53—0,51 = 0,02лЬкр (зерна 4 и?), т. е. величину, в 2 раза меньшую, чем в группах I и III.

В группе IV, где образовалась одна спираль, глубина среза уве­личилась в 4 раза и стала равной 25S06 при соответствующем умень­шении длины царапины в 4 раза до величины 0,01nZ)Kp

Естественно, что при равной производительности съема обраба­тываемого материала (все варианты с этой точки зрения кинемати­чески тождественны) изменение глубины среза с физических позиций неравноценно. Для абразивных зерен, имеющих неблагоприятную форму передней поверхности, характеризуемую большими значе­ниями отрицательных углов, варианты, в которых глубина среза на каждое зерно увеличивается, а дуга контакта уменьшается, предпочтительны. Напряжения на зерне и время износа (контакта) с обрабатываемым матепиалом при возрастании глубины среза
уменьшаются, что благоприятно отражается на стойкости инстру­мента. Благоприятным этот вариант следует рассматривать и с по­зиций увеличения числа зерен, снимающих стружку, и относитель­но уменьшения величины валиков, вытесняемых из царапины, по сравнению с площадью самой царапины. Таким образом, фактиче­ская производительность шлифования из-за изменения своеобраз­ного КПД стружкообразования будет в этих группировках также неодинаковой.

Однако не во всех случаях увеличение глубины среза на зерне следует рассматривать с благоприятных позиций. Если абсолютное увеличение сил на зернах превысит некоторую величину, большую усилий удержания их в связке, это может вызвать повышенный расход абразивного материала из-за усиления степени вырывания зерен с поверхности шлифовального инструмента.

Очевидно, для эксплуатации алмазных кругов на металличе­ских связках, когда и прочность зерен, и степень их удержания выше, чем в других инструментах, указанные обстоятельства могут быть использованы с наибольшим эффектом.

Отметим дополнительно, что варианты группировок 1, II, III, IV рассматривались при соблюдении соотношения скоростей вра­щения инструмента и детали, т. е. при К = const, что может быть достигнуто при изменении К-1 в группах путем компенсации значения коэффициента К-л.

При переходе от группы I к более благоприятной по физическим условиям резания группе IV величина Кг = пкр : пр возросла с

1,4 до 4,04, т. е. практически в 4 раза. Увеличивать значение Ко следует за счет уменьшения диаметра DKp или увеличения dp, или изменения их соотношений, чтобы сохранить неизменным ЦКр и vp ДЛЯ исключения ВЛИЯНИЯ относительной скорости движения t’np на кинематический процесс и для выявления влияния отношения /г, ф : пр в «чистом» виде.

Итак, установлено существенное влияние целочисленного зна­чения Ко на кинематику процесса шлифования. Рассмотрим далее, какое влияние оказывает дробная величина К2- Уже указывалось, что в выражении Ко — А, 04, где А — целое число, равное 1, 2, 3 и т. д., дробная часть 0,4 определяет величину шага между цара­пинами и вместе с величиной А определяют очередность их разверты­вания. В разобранном примере развертывание царапин происходило на каждой из спиралей, образованной зернами 1—4, строго последо­вательно, одна за другой. Определим начальные точки касания четы­рех зерен ролика с поверхностью шлифуемого круга при К2 =• 1,2 и относительно близких значениях К.

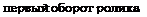зерно 1: 1,2 х 0 = 0лПкр зерно 2 : 1,2 х V4 = 0,ЗлПкр ■-зерно 3: 1,2 х % = 0,6лПкр зерно 4 : 1,2 х 3/4 = 0,9лДф

зерно 1: 1,2 х 1 = 1,2лЦф зерно 2: 1,2 х 11/4 = 1,5лДф зерно 3: 1,2 х 12/4 = 1,8яДф зерно 4 1,2 х 13/4 = 2,1яДф

И Т. д.

Покажем построчно последовательность развертывания царапин по поверхности обрабатываемого круга с указанием сверху номера зерна, а снизу — числа оборотов ролика:

12 3 4 0—0,3—0,6—0,9 —	12 3 4 -0,2—0,5—0,8—0,1
1 оборот	2 оборота
12 3 4	12 3 4
—0,4—0,7—0,0—0,3	0,6—0,9—0,2—0,5
3 оборота	4 оборота
12 3 4	12 3 4

—0,8—0,1—0,4—0,7 —0—0,3—0,6—0,9 и т. д. 5 оборотов 6 оборотов

Как видно из построчной развертки и рис. 28, число царапин, укладывающихся на окружности круга, не равно отношению 1 : (1,2—1) = 5. В данном случае царапины группируются по иному, чем в предыдущем примере, закону, образуя в связи с этим так называемую звездочку.

Из построчной развертки устанавливается, что за каждый обо­рот ролика зерна 1—4 наносят на поверхности круга царапины шагом Ш = 0,3 доли окружности, однако при втором обороте эти царапины не попадают в начальные точки и смещаются по отноше­нию к исходным на величину г/3 шага, т. е. на 0,2, располагаясь правее царапин, ими ранее образованных (для зерна 1 эти значения равны 0 и 0,2, для зерна 2 — 0,3 и 0,5 и т. д.). При этом в конце второго оборота царапина от зерна 4 окажется справа от царапины

1 4

зерна 1 (0 и 0,1) всего на V3 Ш — 0,01. При такой последовательнос­ти нанесения царапин при третьем обороте ролика зерно 3 образует

1 2

царапину в положении 0; зерно 4 — в положении 0,3 и т. д. Эти царапины по сравнению с первыми углубились в радиальном на­правлении в связи с тем, что ролик совершил 2,5 оборота, на величи­ну 2,5So6- Итак, через 2,5 оборота цикл замкнулся. На поверхнос­ти круга образовалось 10 точек (с шагом 0,1, а не 0,2), по отношению к которым симметрично располагаются царапины различных зерен. Например, для точки, расположенной на 0,3 окружности, эти цара­пины будут наноситься при первом обороте ролика (0,25 оборота) зерном 2, при третьем обороте (2,75 оборота) зерном 4, при шестом обороте (5,25 оборота) вновь зерном 2 и при восьмом обороте (7,75 оборота) вновь зерном 4 и т. д. Зерна 2 и 4 сгруппировались и об­
разуют радиально углубляющиеся царапины по отношению к не­четным начальным точкам 0,1—0,3—0,5—0,7—0,9, а зерна 1 и 3 — по отношению к четным точкам 0—0,2—0,4—0,6—0,8.

Глубина резания, приходящаяся теперь на каждое зерно, со­ставляет 2,5So6- Эту же величину можно вычислить следующим пу­тем. В точке 0,3 (jiDKp) после зерна 4, которое прошло эту точку при третьем обороте, зерно 2 прошло ее при шестом обороте. За этот период было сделано V4 третьего оборота +8/4 четвертого и пятого оборотов +V4 шестого оборота, т. е. всего |0/4 = 2,5 оборота ролика, и глубина врезания при этом составит 2,5So6.

В рассмотренном примере после окончания периода врезания длина, проходимая в среднем каждым зерном, составит /ц = = 0,1jiDkp, а максимальная глубина врезания — 2,5So6. Таким образом, видно, что существенно изменились соотношения длин царапин и глубин среза в рассмотренных двух простейших примерах (рис. 27 и 28).

При Кі = 1,04 длина стабилизированных царапин составляла 0,4яДф, а их глубина — 6,25So6; при К2 = 1,2 соответственно 0,1лОКр (в 2,5 раза больше) и 2,5So6 (в 2,5 раза меньше).

В первом случае, если бы речь шла о шлифовании метал­лов, стружки снимались бы толще и короче, во втором — тоньше и длиннее.

В случае образования звездочки (К2 = 1,2) правящий ролик работает таким образом, что усилия на каждом зерне из-за умень­шения глубины среза значительно снижаются, а путь, проходимый зерном в обрабатываемом теле, пропорционально возрастает, в результате этого абразивное воздействие шлифовального круга на ролик усиливается. Здесь заранее трудно сказать, увеличится ли в последнем случае стойкость правящего ролика, так как на алмазы воздействуют два взаимоисключающих (с точки зрения износа) и различных по физическому воздействию на зерно фактора: сниже­ние величины динамической (ударной) нагрузки от сил резания — царапания и одновременное удлинение пути резания по абразиво­содержащему материалу.

Рассмотренные примеры неравноценны также в отношении формы и микрогеометрии образованной поверхности. При правке методом «летучих» резцов не получается строгой цилиндрической поверхности у шлифовального круга.

В одном случае в результате кинематики движения образуются архимедовы поверхности (одна или несколько в зависимости от группировки царапин), в другом — звездочка, выступы и дно цара­пин которой также лежат на архимедовых спиралях.

В разобранном примере (рис. 28) четные впадины (в начальных точ­ках 0,2—0,4— …) образуют одну, а нечетные (вточках 0,1—0,3—… …) — другую спирали. Указанное расположение выступов и впадин (дна) царапин лучше видно из положения центров мгновенного вращения роликов на архимедовой кривой, соединяющей эти центры в начальных точках окружности круга.

Очевидно, шлифовальный круг — звездочка со впадинами, из­меряемыми долями миллиметра, целесообразнее использовать для чернового и предварительного шлифования, так как ограниченное число зерен выступов позволяет снимать металл с повышенными глу­бинами резания, не опасаясь прижогов поверхности, как при шли­фовании кругами с прерывистой поверхностью. Небольшая степень перекрытия зерен выступов не обеспечит в этом случае низкой шероховатости обрабатываемой поверхности.

В свою очередь шлифовальный круг с несколькими архимедо­выми поверхностями с увеличением глубины резания плавно вводит зерна в работу, разновысотность зерен здесь существенно меньше, а класс шероховатости выше.

Из табл. 10 следует, что для всех группировок зерен /цйц = = const. Эта зависимость вытекает из постоянства среднего объема материала, снимаемого за каждый оборот с абразивного круга во второй фазе правки при установившемся процессе резания.

Поясним все сказанное выше расчетом. Дано: /С2, Z(l Scб, АЬ, тогда средний объем материала, снимаемый элементарным цилин­дром ролика диаметром dp и шириной АЬ, на котором размещено Z„ зерен, за один оборот ролика будет

Д№ср = nD^KAbSrf. (2.4)

Объем материала круга, удаляемый из одной царапины, равен Ablnhu и на все зерна Z0

ДИ7ср = Д blahaZoKv (2.5)

Приравняв (2.4) и (2.5), получим

= (2-6)

Из выражения (2.6) следует, что при Z0 и Sn6 — const средняя боковая площадь среза /ср = йц/ц тоже постоянна.

При /ц/гц = const множители /ц и /гц существенно изменяются из-за кинематической группировки царапин. Длина царапины при этом

(2.7)

Здесь Ш = (/(2 — А) — относительный шаг между царапинами, равный по абсолютному значению дробной части параметра Л2 (при этом, если /С-2 > 0,5, то в качестве относительного шага берется дополнение до единицы ИГ = 1 — Ш, так, например, Ш = 0,78, тогда в качестве величины относительного шага прини­мается ИГ = 0,22); А — целочисленная часть (перед запятой) пара­метра К2; Zrp — число зерен из числа Z0, образующих царапины, располагающихся на одной спирали.

Подставив (2.7) в (2.6), получим расчетную глубину царапины:

Если число спиралей, образованных царапинами, равно псп, то усредненная глубина резания, приходящаяся на одно зерно, будет

Приведенный анализ позволяет прийти к важному для практики шлифования выводу о том, что при использовании явления группи­ровки царапин возможно формирование рабочей поверхности круга одной и той же характеристики, пригодной для чернового и чисто­вого шлифования на одном рабочем месте без перестановки абразив­ного инструмента. Для осуществления процесса достаточно иметь регулируемый привод вращения правящего ролика. Целесообраз­ность совмещения чистового и предварительного шлифования на одном рабочем месте очевидна.

Однако практическое значение метода этим не исчерпывается, он требует нового подхода к конструированию правящих инстру­ментов. Очевидно, нет необходимости для типового процесса шли­фования однородной продукции использовать правящие ролики со стандартной укладкой алмазов по всей поверхности инструмента в шахматном порядке. Целесообразнее их сгруппировать в избран­ных точках цилиндрической или фасонной поверхности правящего ролика (например, в точках 4, 6 и т. д., как показано на рис. 27 и 28), расположить на разной высоте (с целью более равномерного распределения глубины шлифования) или с переменным шагом (для гашения вибраций) в соответствии с заранее проведенным кине­матическим расчетом.

Целесообразно также разработать алмазные вставки специальной конструкции для пайки или механического крепления в корпусе инструмента. В последнем случае на базе одного нормализованного корпуса с заранее образованной системой пазов можно создавать различные расчетные комбинации расположения стандартных не- перетачиваемых правящих элементов (вставок).

Овладение методом кинематического расчета процесса правки сулит дополнительные резервы для повышения производительности обработки и улучшения качества изготовляемой продукции.

Кинематика шлифования круглой детали. Рассмотрим далее кинематику врезного круглого наружного шлифования детали аб­разивным кругом. Обозначим

где Од, пд, (ід— соответственно скорость вращения, число оборотов и диаметр шлифуемой детали.

По сравнению со схемой правки шлифовального круга роликом здесь диаметр шлифовального инструмента больше, чем у обрабаты­ваемой детали, выше скорость вращения и число оборотов. Однако это обстоятельство существенным образом не меняет схему нанесения, форму и расположение царапин

Рассмотрим схему нанесения царапин на деталь шлифовальным кругом, имеющим, по-прежнему, 4 симметрично расположенные режущие точки. Рассмотрим последовательность расположения царапин на поверхности детали при /(2 = 5:

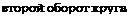зерно 1: Чъ X 0 = Олdu зерно 2 : Чй X ‘/4 = 0,05ndB зерно 3: V6 X 2/4 = 0, Юлс1й зерно 4: [1]/5 X 3/4 = 0,Ъпйа зерно 1: Чъ X 1,0 = 0,20лс(д зерно 2: l/6 X м/4 = 0,25ndB зерно 3: Ч6Х, а/4 = 0,30лс(д зерно 4: VR X,3/4 = 0,35лс1д и т д.

Царапины на деталь наносятся последовательно всеми зернами шлифовального круга с шагом Ш = 0,05.

За полный оборот детали шлифовальный круг сделает пять полных оборотов и нанесет 20 царапин, при этом центры вращения сместятся на Д = 55об. Царапины будут располагаться на спирали с шагом Д = 5S06. Таким образом, имеется полная аналогия обра­зования царапин с таковым, рассмотренным выше в примерах (см. табл. 10, группа IV). При шлифовании детали также, незначительно в меньший промежуток времени происходит на первом этапе пред­варительное врезание до момента слияния царапин, затем на втором этапе — стабилизация процесса шлифования, характеризуемая по­стоянством длины, глубины и ширины среза, т. е. объемом снимаемо­го материала определенным зерном шлифовального круга при всех последующих циклах его врезания.

Покажем также, что дробная часть величины параметра /(2, влияя на длину царапины, не изменяет схему нанесения царапин. В самом деле, при К2 = 5,208 расположение царапин на поверхнос­ти детали с относительным шагом Ш по-прежнему будет последова­тельным:

1 2 3 4 1 2 3 4 1

0—0,048—0,096—0,144 —0,192—0,240—0,288—0,336—0,384 и т. д.

ветственно уменьшится или возрастет шаг между царапинами Ш и вновь дуга контакта будет равна длине царапины, которая в свою очередь равна величине Шягід.

Таким образом, во всех приводимых в литературе схемах, изображающих контакт зерен шлифовального круга с деталью при круглом врезном шлифовании, допускается ошибка, если на дуге контакта изображается одновременно несколько кон­тактирующих зерен и если длина дуги контакта при установив­шемся процессе правки переменна.

Таким образом, за площадь контакта для правящего ролика с правильной укладкой алмазов следует принять произведение средней длины царапины на фактическую ширину контакта инстру­мента с деталью:

FK = /ц5ф = ШлЯкрВф. (2.10)

Здесь FK — площадь контакта шлифующего инструмента с деталью, мм2; Вф — фактическая ширина контакта круга с деталью, мм.

Отметим еще одну особенность врезного шлифования. Как при шлифовании — правке абразивного круга алмазным роликом, так и при шлифовании детали кругом цикл обработки, равный времени съема некоторого объема материала со всей поверхности изделия, существенно больше одного оборота шлифующего инструмента.

Так, на рис. 27 и 28 после завершения времени предварительного врезания этот цикл равен в первом случае 25 оборотам, а во втором— 10 оборотам ролика (параметр К2 = 1,04 и /С2 = 1,2). При шлифовании детали в рассмотренном примере при /(2 = 5 шли­фовальный круг совершает 5 оборотов на один полный оборот де­тали. Очевидно, подача на оборот круга S0б, строго говоря, не мо­жет быть расчетным параметром, в зависимости от которого должны определяться функционально зависимые от геометрии среза вели­чины процесса шлифования. Прежде всего Saб не может отождест­вляться с глубиной резания, это только часть глубины. В табл. 1J показано, что глубина резания соответствует расстоянию между спи­ралями, являющимися геометрическим местом расположения дна царапин на формируемой поверхности резания, и равна Лц = tpe3 = ns

= п ‘So6 =——— —, где П’ — множитель, равный числу оборотов

Псп

шлифующего инструмента, необходимых для прохождения одной смежной спирали под другой.

Теперь можно обобщить методику решения кинематической задачи при врезном шлифовании. Для этого необходимо заранее знать или определять отношения Кі, Кі К-Л, число режущих зерен, расположенных на одной окружности вращения; законы их распре­деления по длине окружности и ширине шлифующего инструмента; направление вращения инструмента и детали; величину поперечной подачи Боб-

Расчет можно проводить графическим или математическим путем и включить в него следующие моменты:

а) установление очередности и закономерности нанесения цара­пин шлифующим инструментом на деталь на первом этапе — этапе врезания;

б) определение продолжительности цикла врезания, выраженной временем, числом оборотов шлифующего инструмента, числом цара­пин до их слияния в одну бороздку;

в) определение параметров установившегося процесса шлифова­ния или правки на втором этапе: длины царапин, теоретической глу­бины и ширины среза, приходящихся на отдельные рабочие зерна, площади контакта и числа зерен, одновременно контактирующих с обрабатываемым материалом;

г) исследование (проработка) наивыгоднейшего варианта отно­шений Кг, К2, Ка, величины подачи, направления вращения инстру­мента и детали с точки зрения производительности процесса, мини­мальной нагрузки на зерна (повышения стойкости инструмента) и обеспечения необходимой шероховатости шлифуемой поверхности;

д) получение исходных данных для размещения зерен в PC пра­вящего ролика, обеспечивающих оптимальный вариант решения кинематической задачи, а также назначение величины К2 для прав­ки и шлифования;

е) разработку рекомендаций по строгому обеспечению парамет­ров кинематического процесса, в первую очередь отношения чисел оборотов К2 при правке и шлифовании;

ж) получение исходных данных для проектирования и установ­ления замкнутой кинематической цепи: правящий ролик — шлифо­вальный круг — деталь по адаптивной или жесткой схеме управления.

К сожалению, в литературе отсутствуют указанные кинема­тические расчеты. Частично они используются в утилитарных целях, например для расчета дуги контакта, числа контактирую­щих зерен при анализе других задач, чаще всего связанных с опреде­лением параметров среза, усилий шлифования, шероховатости по­верхности.

Из кинематически неделимой цепи: правящий инструмент — шлифующий круг — деталь рассматривается лишь последняя кине­матическая пара. Определяющее значение правящего инструмента, с помощью которого вышлифовывается форма и образуется микро­рельеф шлифовального круга, придающие ему основные режущие свойства и предопределяющие в дальнейшем кинематические и динамические параметры процесса обработки самой детали, при этом остается в тени и не выясняется должным образом.

_ *Р

Недопустима и недооценка роли кинематической стороны в изучении процесса шлифования. С полным основанием можно утвер­ждать, что при данных характеристиках правящего инстру­мента, шлифующего круга и материала детали исходные параметры процесса (производительность, качество обработки, расходы на инструменты, а значит, себестоимость операции шлифования) яв­

Кз = при правке; Кг = ; Кг=^р; К3 = —р~ при обра-

tip 1>д Пд Од

ботке детали и при соответствующих выбранных (непрерывных или ступенчато изменяющихся) подачах Snon и направлениях движения инструментов и обрабатываемых тел.

Кинематические параметры в этих условиях однозначно опре­деляют динамику взаимодействия инструмента и детали, необ­ходимые практические следствия шлифования. Более того, если ранее созданные металлорежущие станки с адаптивным управле-

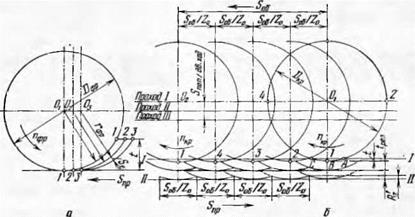
Рис. 29. Схема стружкообразования при фрезеровании (а) и продольном врезном шлифовании (б).

нием процесса резания были основаны на стабилизации какого — либо динамического параметра (например, силы Р или Рг), то в настоящее время основой адаптивного управления процессом шли­фования должно стать поддержание постоянными кинематических параметров К2 и Snon и выбор (изменение) их по программе в тече­ние одного цикла шлифования и при обработке различных деталей.

Схема стружкообразования при плоском шлифовании. В ли­тературных источниках часто для иллюстрации продольной формы стружки, снимаемой при шлифовании, пользуются схемой, анало­гичной схеме продольного фрезерования.

Покажем, что схема «летучих» резцов кинематически не всегда тождественна указанной схеме.

На рис. 29 показаны рассматриваемые схемы стружкообразо­вания при фрезеровании и шлифовании.

Используем для последней схемы расчет длины царапины, аналогично тому, как это было сделано для круглого врезного шлифования. Для простоты построений примем, что зерна равно­мерно размещены на окружности круга, а продольную форму царапин образуем дугой окружности. Время контакта избранной точки окружности круга диаметром DKp равно времени прохождения

ее по дуге АВС:

тк = 2 Vt (Окр— /2) гГр-

Тогда длина траектории точки А (от входа до выхода), измеренная вдоль вектора подачи на некотором уровне /—I,

Ттр = SnpTK = 2Snp VЖРV-1. (2.11)

Для шлифования величина (<£DKp и значением /2 под корнем мож­но пренебречь.

Относительное смещение центра вращения круга 01 за один обо­рот в точку 02 составит

Sqб — — Snp/flap = 5прЗХ ДкрЦ * —

Отношение длины царапины Тц к величине смещения центра вращения круга вдоль шлифуемой поверхности за 1 оборот

Поскольку глубина внедрения t существенно меньше диаметра абразивного круга, числитель выражения (2.12) существенно больше знаменателя. Таким образом, отдельно взятое зерно на по­верхности детали оставляет лункообразные царапины, не соприка­сающиеся друг с другом, с шагом, равным Sot.

Чтобы лунки слились, необходимо увеличива ь глубину вреза­ния t до значения tpe3 и количество режущих зерен Z0, распо­ложенных на одной окружности вращения. Тогда суммарное число царапин на длине шага S0 должно быть не менее S0 : = Zmin.

■ ■ Найдем минимальное количество царапин для их слияния в одну бороздку. Для этого возведем в квадрат выражение (2.12):

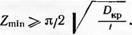пЮ

KJ)

откуда

(2.13) і Используем уравнение (2.13) для расчета минимального коли­чества зерен, укладываемых на некоторый гипотетический цилин­дрический круг в шахматном порядке, со средними расстояниями между ними /м.

На окружности круга диаметром DKp будет размещено зерен

•7 ЛЯр

Z0 = —■, откуда

= ^ (2.14)

Формула (2.15) показывает, что при создании такого круга не­обходимо расстояние между зернами выдерживать в соответствии с глубиной шлифования. Так, например, при снятии припуска t = = 0,01 мм и при расстоянии между зернами /м = 1 мм достаточно иметь Zmin 100;шт., а диметр круга DKp ~ 30 мм.

Размеры круга увеличатся, если в основу расчета положить условие получения продольных неровностей, не превышающих заданную величину Rz. На рис. 29, б показано, что зерна 1, 2, 3, 4 шлифовального круга при некоторой глубине резания (рез > t образуют перекрывающие друг друга царапины, длина которых Тц = S0rJZlt. После окончания шлифования по отношению к уров­ню поверхности детали II—II остаются неровности, равные Rz. Их величина не превышает высоту стрелки хорды АС при t = Rz. Тогда для гарантии получения шероховатости, не превышающей Rz, шаг между зернами не должен быть больше дуги АВС, т. е.

ІМ = АВС = 2 V RZDKP, (2.16)

откуда число зерен

Если Rz = 0,5 мкм и конструктивно диаметр круга DKp = 500 мм, то /м = 2 У 0,25 = 1,0 мм.

В приведенной упрощенной методике подбором зернистости кристаллов абразива, определяющей шаг /м » dn, и диаметра круга решается вопрос обеспечения шероховатости поверхности. Более точно задача может быть решена при учете влияния величины про­дольной подачи, однако в данном случае это не является нашей целью.

Рассмотрим случай, когда вершины зерен шлифовального круга или правящего ролика располагаются на разной высоте, а плотность их по глубине слоя переменна.

При известном значении глубины резания число зерен в объеме РПС И^рпс = ndptpe3 В может быть подсчитано по уравнениям (см. табл. 8), определенным на основании аппроксимации эксперимен­тальных точек, полученных по царапинам на плоском клине путем подстановки ht — /рез — Число зерен, участвующих в процессе реза­ния для той же глубины, можно рассчитать по уравнениям (2.1) и (2.2).

Картина распределения вершин зерен по ширине шлифования до глубины hn определяется по профилограммам царапин (см. рис. 24).

Вероятностная оценка числа зерен, расположенных на одной окружности зернистостью Вариант Глубина, мкм Zj, ШТ A b. мм Ks — Qg, CM* Вероятность 0 | 1 Но = 12 37,4 0,027 3,4 0,20 81,8 16,5 — 21 91,1 0,040 8,3 0,72 48,7 35.0 Ы = 30 144,8 0,057 13,2 1,64 19,4 31,8 hi = 50 263,8 0,094 23,9 4.91 0,7 3,5 hi = 100 561,8 0,189 51,0 21.20 — — и ho = 12 37,4 0,064 3,4 0,48 61,9 29,7 hn = 21 91,1 0,083 8,4 1,52 22.1 33,3 hi =30 144,8 0,100 13,3 2,89 5,5 16,0 hi =50 263.8 0,130 23,9 3,29 3,7 12,3 ht = 100 561,8 0,180 51,0 20,20

Очевидно, до глубины h0 вершины зерен по ширине шлифования не перекрываются, и можно считать, что число зерен, располагаю­щихся на одной окружности, Z0 = 1. Тогда рассмотренные выше слу­чаи кинематического взаимодействия ролика и круга (см. рис. 27 и 28), шлифовальног і круга и плоской детали (рис. 29) сводятся к схеме нанесения царапин одним зерном.

В интервале глубин от /г,, до /гп, когда царапины сливаются по ширине шлифования, вероятность появления нескольких царапин, расположенных в затылок друг другу, возрастает. При этом опре­деленная разновысотность зерен по отношению к окружности враще­ния сохраняется.

Оценим вероятность появления т = 1, 2, 3 … вершин зерен в затылок друг другу на поверхности элементарного диска ди­аметром dp и шириной ДЬ, соизмеримой со средней шириной вер­шин зерен на рассматриваемой глубине ht.

Для простоты расчетов в одном варианте (вариант I) будем считать, что вершины зерен имеют вид конусов с углом при вер­шине 2а, как это показано в работе [57]. В другом варианте (вариант II) проведем расчеты величины АЬ исходя из предположения, что зерна представляют собой шарики диаметром cla. В первом случае величина АЬ приближенно определяется из выражения

АЬ = V3/it tg а. (2.18)

Здесь V3 — центр группирования оснований «треугольных» вершин зерен, распределенных по высоте ht по прямолинейному закону.

Во втором случае для радиусных вершин зерен имеем формулу

Д6 = 2 /Щ = — JL. |/ад. (2.19)

Таблица 11

?	4	5	в	7	8	9	10	П
1,7 12,6	3,0	0,5	—	—	—	—	—	—	—
26,1	14,3	5,8	2,3	0,6	—	—	—	—	—
8,6	14,2	17,6	17,5	14,5	10,3	6,4	3,5	1,8	0,8
—	—	—	—	—	—-	—	0,1	0.3	0.6
7,1 23,8	1,1 12,7	0,1 4,8	1,5	0,4	—	—	—	—	—
23,2	22,3	16,2	10,1	4,5	1,9	0,7	—	—	—
20,0	22,1	18,2	12,0	6,6	3,0	1,3	0,4	—	—
—	—		—	—	—	0,1	0,3	0,5	1,0

вращения для алмазного правящего ролика диаметром 70, шириной 5 мм. АСК 250/200, 100%

Рт . %. при т. равном

Формулы (2.18) и (2.19) отражают увеличение расчетной величины Дb и возрастание вероятности попадания зерен в затылок друг дру­гу по мере углубления в ПС абразивного круга.

Определив по данным царапания клина (см. рис. 24) для раз­личных значений ht методом проведения касательной общее коли-

у

чество режущих зерен в слое Z, и среднюю их плотность в »

кр

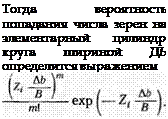
где nDKpB — площадь поверхности цилиндра круга диаметром DKp и шириной В, можно вычислить параметр Пуассона

as = ^ДЬлДф — Z, (2.20)

(2.21)

В табл. 11 для рассматриваемых вариантов (I и II) приведены расчеты вероятности размещения неперекрытых (рабочих) зерен на одной окружности вращения на разных уровнях РПС.

Для простоты расчетов примем размер d0 = 256 мкм. Глубину слоя hi изменяем в пределах от 12 до 100 мкм. В первую очередь нас интересуют глубины hi — h„ = 12 мкм и hn = 21 мкм (см. рис. 25), а также А,- = 30 ч — 50 ч — 100 мкм. Число рабочих зерен определя­лось по уравнению параболы табл. 9.

В расчетах приводятся значения ДА, число зерен на 1 см2 на дан­ном уровне РПС круга, параметр Пуассона as и вероятность Рт

для различных значений т. Устанавливается, что до глубины слоя, равной ftfl, на одной окружности вращения в большинстве случаев находится по одному зерну. Для варианта II (вершины шариков) имеется 7% участков ДЬ (окружностей), на которых размещено 2 зерна, а для варианта I — только 1,7% таких окружностей. На большинстве участков Дb (соответственно 81,8% и 61,9%) вершин зерен нет, в результате шлифовальный круг при внедрении на глу­бину ht = 12 мкм оставляет неперекрытые по ширине царапины (см. схему рис. 23, сечения 1—1 и 2—2).

Для последовательно увеличивающихся глубин число зерен, расположенных в затылок друг другу, возрастает. Так, для /іп = = 21 мкм имеются окружности с 6—8 зернами, хотя большинство из них по-прежнему содержит 1—2 режущие вершины. И только при больших глубинах шлифования (Л,- = 0,03 ч- 0,05 мм) в большинст­ве случаев на одной окружности находится 2—4 зерна, хотя имеются «цилиндры» ДЬ, на которых размещено 9—11 рабочих вершин.

При глубине слоя h[ = 0,1 мм наибольшее число зерен на одной окружности соответствует модальному значению распределения а» 20, а практический интервал размещения составляет мини­мально 8—10 и максимально 28—30 зерен.

Интересные результаты получены при т = 0. Условие непо­падания зерен на заданный интервал ДЬ сохраняет свое значение до глубин слоя ht = 50 мкм, т. е. до значительно больших глубин, чем это следует из опытов по царапанию. Так, при ht — 0,1 ч — Ч — 0,13 мм вероятность отсутствия режущих вершин составляет 1— 4%, т. е. практически значимую величину. Для рассматриваемого ролика перекрытие (слияние) царапин наступает при /гп = 21 мкм, что следует объяснить явлением вытеснения металла из царапины на боковые ее стороны и увеличением, таким образом, эффекта пере­крытия.

Тем не менее на практике при изготовлении партии роликов для шлифования беговых дорожек колец двухрядных подшипников качения наблюдались случаи, когда тот или иной ролик начинал образовывать риски на обработанной поверхности. Очевидно, частная реализация вероятностной картины распределения зерен по поверхности ролика в данном случае была неблагоприятной, а дополнительный эффект бокового течения металла не смог ком­пенсировать отсутствие перекрытия зерен, размещенных на смеж­ных окружностях вращения. После доводки ролика по вершинам с помощью алмазного круга риски исчезли, шероховатость обрабо­танной поверхности под следующую доводку становилась прием­лемой.

Аналогичную задачу можно решить и для шлифовальных кругов большего диаметра, чем в рассмотренном примере, с роликом от­носительно малых размеров. С точки зрения шероховатости обра­батываемой поверхности при врезном шлифовании ограничивающим моментом по-прежнему будет являться вероятность отсутствия зерен на участке круга шириной Аb и явление разновысотности зерен.

Увеличивая диаметр, удается добиться уменьшения разновысот — ности зерен по ширине и окружности шлифовального круга, в ре­зультате чего и вероятность непопадания зерен на окружность вращения снижается до несущественных величин (практически невозможность наступления данного события). Однако в большин­стве случаев при врезном шлифовании не удается уменьшить шеро­ховатость ниже 6—7-го классов. Так, при шлифовании врезным методом шеек коленчатых валов диаметры кругов достигают 900— 1100 мм. Тем не менее появление отдельных рисок на галтелях шеек является распространенным видом брака на этой операции.

Более перспективным и проверенным на практике является метод притупления вершин зерен до определенного уровня с по­мощью правящих инструментов. Этот метод приемлем для шлифо­вальных кругов любого диаметра и обеспечивает шероховатость шлифуемой поверхности при врезании до 8—9-го классов.

Установлено (см. рис. 29), что в абразивных кругах в резуль­тате пуассоновской статистики распределения на элементарных окружностях вращения может находиться различное количество режущих вершин зерен: от одного зерна до нескольких десятков и даже сотен штук. Тогда при плоском шлифовании в случае малого числа зерен (Z0 <; 10) продольная подача должна быть ограничена по величине таким образом, чтобы суммарная длина царапин от все­го количества Z0 несущественно отличалась от величины So6.

Так, из формулы (2.13) следует, что если Z0 = 1, то

царапин необходимо, чтобы врезание происходило на величину, превышающую диаметр круга. Реально царапины на участках ДЬ при Z0 = 1 не сливаются, что приводит к появлению необрабо­танных участков шлифуемой поверхности. Правда, при шлифовании с боковой поперечной подачей эти необработанные участки срежутся теми участками АЬ, где число зерен существенно больше. Это про­изойдет в том случае, если участков с Z0 = 1 будет не ] слишком много.

Решим следующий пример. Пусть DKр = 450 мм, а глубина продольного шлифования t = 0,5 мкм, тогда

ZmXn>^V9- 10*^1000 шт.

Очевидно, абразивный круг любого диаметра зернистости на глу­бине РПС ht = 0,5 мкм не удовлетворяет этому условию. При шлифовании с такой глубиной на поверхности детали образуются отдельные риски. Чтобы они слились и образовалась новая шли­фованная поверхность по ширине, необходимо, чтобы они вре­зались на величину t >• hn. Так, для ролика диаметром 70 мм зернистостью АСК 250/200-100% эта глубина составляет h„ = — 0,021 мм и Zmm ;> 1,5 Y33,3 • 102«87 шт. Расчеты показывают

(см. табл. 11), что на этой глубине ни на одной окружности цилинд­ра с шириной АЬ такого количества зерен не имеется. Очевидно, для слияния царапин по длине (по ширине они уже слились) необ­ходимо врезаться еще глубже.

Возьмем hc = 0,1 мм, тогда условие Zmin >• 12,5 полностью удовлетворяется (см. табл. 11). Действительно, на такой глубине слоя минимальное количество зерен на одной окружности с веро­ятностью Рт> 1 % превышает эту величину.

Таким образом, приходим к следующим выводам:

1. Перекрытие царапин по ширине наступает при меньшей глубине, т. е. значительно раньше, чем по длине (0,021 < 0,1 мм).

2. Глубина врезания шлифовального круга не зависит от ве­личины продольной и поперечной подачи и определяется законом размещения зерен в объеме абразивного слоя и формой вершин абразивных зерен.

3. Абразивные зерна, расположенные в РПС до глубины вре­зания, находятся в наиболее неблагоприятных условиях, так как на одной окружности вращения их размещается наименьшее коли­чество с наибольшей разновысотностью. В этом слое образуются наибольшие по сечению и длине стружки, возникают наибольшие усилия резания и наибольшая степень износа зерен.

4. Для вершин зерен, находящихся в слое предварительного врезания, в известном смысле совершенно безразлично, в каком режиме работает шлифовальный круг. При чистовом и черновом шлифовании они нагружены одинаково. Иначе говоря, стойкость зерен в этом слое невозможно увеличить за счет облегчения режимов резания.

Выводы, полученные на примере продольного врезного шли­фования, можно с полным основанием распространить и на круглое врезное шлифование. Здесь также наибольшую трудность состав­ляет обеспечение слияния царапин в единую борозду по длине окружности шлифующего тела, и происходит это также на большей глубине врезания, чем это требуется для перекрытия царапины по ширине (см. рис. 27 и 28).

Все затруднения с перекрытиями царапин связаны, по сути, с двумя основными факторами: числом зерен на окружности и разновысотностью вершин на них, неравномерность распределения которых предопределена пуассоновским законом распределения частиц в объеме, а недостаточное их число в наружном слое — параболическим законом распределения вершин зерен по глубине PC абразивных инструментов.

Как же изменится глубина врезания, если перейти от плос­кого врезания (только с вертикальной подачей) к обычному плос­кому шлифованию? Если после каждого двойного хода стола кругу придать боковое смещение на некоторую часть его ширины (попереч­ную подачу), то произойдет боковое перекрытие элементарных цилиндров вращения шириной АЬ, содержащих различное число зерен (и малое и большое). Если теперь перекрыть те участки ши­
рины круга ЛЬ, в которых раньше не обеспечивалось слияние ца­рапин из-за малого числа зерен Zn и требовалось более глубокое врезание круга участками ЛЬ с большим числом зерен, то послед­ние дополнительно подрежут оставшиеся не снятыми участки шлифуемой поверхности. Тогда глубина врезания будет опреде­ляться не участками ЛЬ с минимальным количеством зерен, а участками с большим количеством зерен и для получения сплош­ной шлифовальной поверхности уже не потребуется столь больших глубин врезания.

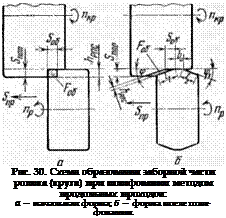Таким образом, при шлифовании методом продольных проходов (круглое шлифование) и методом поперечного смещения при плос­ком шлифовании (что кинема­тически равноценно) происхо­дит разделение функций меж­ду участками ЛЬ круга, имею­щего число зерен, недостаточ­ное для продольного слияния царапин, и участками ЛЬ, имеющими достаточное для этого числа зерен: первые сни­мают часть материала (нано­сят отдельные бороздки), вто­рые — дополнительно дошли — фовывают при следующем проходе поверхность, не сре­занную первыми.

В результате неравномер­ного износа круга по ширине на нем образуются две заборные части, величина которых, как сле­дует из работы [5], определяется глубиной слоя, снимаемого кру­гом при прямом и обратном ходах. Между заборными частями име­ется цилиндрический поясок Ь0, который выполняет зачистную функцию (рис. 30).

Если в на іале резания сразу после правки круг имел строгую цилиндрическую поверхность (рис. 30, с), то в результате ускорен­ного кромочного износа на нем быстро образуется заборная часть (рис. 30, б), которая выравнивает нагрузку по участкам ЛЬ в ре­зультате разделения между ними снимаемого припуска за проход по глубине.

Для нормальной работы минимальная глубина заглубления круга должна обеспечивать на любой окружности зачистного пояска число зерен Z0 >- Zrain, при которых гарантировалось бы слияние царапин по длине за каждый оборот шлифовального круга.

С образованием заборных конусов вершины зерен, расположен­ные вдоль них, в результате неравномерного распределения и не­достаточного заглубления не срезают полностью материал, а ос­тавляют его для участка Ь0. Таким образом, этот поясок прини­мает самое активное участие в резании, совершая не меньшую

работу, чем любая часть заборного конуса. Очевидно, чем шире участок Ь0, тем ниже будет в общем шероховатость поверхности, так как его зерна с большей надежностью перекроют недошлифован — ные зернами заборного конуса части обрабатываемой поверхности. В связи с этим должна существовать минимальная ширина круга, равная /, + Ь0 + /2. которая еще может обеспечить заданную шероховатость, и в которой длина участка Ь0 играет решаю­щую роль.

На практике этот вопрос решается путем простой замены не­оправдавшего себя круга на круг с большей высотой В или сущест­венного снижения производительности за счет уменьшения величины поперечного смещения круга за двойной ход стола.

Расчет глубины слоя круга, участвующего в шлифовании, произво­дится значительно проще, чем при врезном шлифовании. Из рис. 30 следует, что глубина РПС заборной части, участвующего в резании,

Здесь Боб — продольная подача на один оборот круга, мм; t — 5поп — поперечная подача (глубина съема) за ход или двойной ход сто­ла, мм; — длина заборной части, мм; F0в — площадь теоретиче­ского поперечного среза за один оборот круга, численно равная произведению SoeSnon- Сложнее определить глубину среза, при­ходящуюся на зерна, «зачистного» участка Ь0, так как она в отдель­ные промежутки времени колеблется теоретически от 0 до t. Для простоты расчетов ее можно принять в среднем равной hvnc заборной части. Тогда расчетный слой круга, участвующий в реза­нии, по глубине будет равным йРпс, по ширине — /, + Ьй при пря­мом ходе и /2 + Ь0 при обратном ходе. Зная эти величины, несложно рассчитать количество зерен в этом слое по формулам, выведенным по методике подсчета царапин на клине, и выделить режущие зер­на, как ранее указывалось, с помощью касательной.

В качестве расчетной дуги контакта LK будет выступать усред­ненная длина царапин, равная для плоского шлифования Soq/Zq, где Z0 — среднее число зерен на окружностях вращения, рассчитан­ное для заглубления круга на величину t. Оценку колебаний мгно­венного числа зерен на площади контакта можно произвести, ис­пользуя уравнение Пуассона на примере табл. 11.

Теперь, когда прояснилась картина образования шлифованной поверхности в результате совокупного слияния царапин по длине и ширине, можно заключить, что схема продольного цилиндрического фрезерования (см. рис. 29) не годится для описания кинематики процесса шлифования. Нет здесь и правильно срезаемой запято- образной по форме стружки, картина размещения одновременно нескольких зерен на дуге контакта также иная.

При фрезеровании глубина снимаемого слоя t и число режущих зубьев 2фр соотносятся между собой таким образом, что заведомо отпадают затруднения с перекрытием царапин.

продольной подачи Sоб здесь значительно меньше, чем при шлифо­вании, и существенно меньше половины длины царапины, в ре­зультате чего возможно кинематически осуществить процесс при числе зубьев, меньшем Zmin-

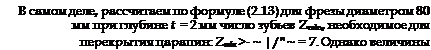Таким образом, при обычном шлифовании всегда /ц Soe и кинематически (по методу образования царапин) эти схемы не тождественны, так как при фрезеровании /ц 5об-

Установившееся в практике фрезерования и шлифования соот­ношение между глубиной шлифования и продольной подачей, от­ражающее указанные неравенства, вытекает из общего требования — обеспечения наивысшей производительности процесса.

Цель фрезерования — снять после литья или штамповки при­пуск, исчисляемый миллиметрами за один проход с максимальной продольной подачей. В связи с этим стремятся разместить максималь­но возможное число зубьев Z(j, p из условия их прочности и работать с максимальным числом оборотов в пределах экономической стой­кости фрезы (или мощности привода).

При больших глубинах фрезерования t даже при ограниченных диаметрах фрез длина дуги АВС (см. рис. 29) столь велика, что по физическим условиям резания (силы, температура на режущих кромках) невозможно выполнить условие So6 > /ц (выгодное с точки зрения производительности). Оно приемлемо для процесса шлифования, для которого важен в первую очередь не обьем снимае­мого металла, а площадь обработки. При этом припуск материала, снимаемый с детали, минимален (десятые и сотые доли миллиметра), г продольная подача на один оборот изделия существенно выше, чем при фрезеровании.

Очевидно, если перед шлифованием поставить те же задачи, что и перед фрезерованием — снимать черновой припуск с изделия (снижая, естественно, подачу на оборот), то схемы стружкообра — зования сблизятся.

Таким образом, в случае силового шлифования, рассмотренные схемы кинематически могут быть тождественными.