Выше была рассмотрена идеализированная модель инструмента, состоящая из зерен одинакового диаметра dcp. Сам круг рассматривался как геометрически правильное тело, не имеющее отклонений от идеальной формы цилиндра или кольца.
При переходе от модели к физическому объекту необходимо учитывать геометрические отклонения размеров зерен от идеального шара, тем более, что в дальнейшем нас будет интересовать положение вершин зерен. Такая оценка отклонения сделана в работе А. В. Королева [41]. Эта оценка указывает на то, что среднее квадратическое отклонение распределения положения вершин зерен над связкой инструмента слабо зависит от распределения размеров зерен в партии, но в значительной степени определяется их средним размером dcp. Автор работы [41] делает вывод о том, что если бы даже все абразивные зерна, выступающие над связкой инструмента, имели бы форму шаров одинакового размера dcp, то и в этом случае разновысотность зерен вследствие разной их глубины заделки была бы велика. При этом дисперсия вершин зерен, выступающих над уровнем связки, составляла бы для зерен равных размеров ои = = 0,29dcp, в то время как дисперсия с учетом рассеивания размеров зерен в партии (по ГОСТ 3649—59) составляет аи = (0,303 — f — — т — 0,306)е? Ср-
А. В. Королев, принимая за базу отсчета средний уровень связки, вынужден говорить о разной глубине заделки зерен по отношению к этой поверхности отсчета. На самом деле, как было показано, центры зерен в матрице жестко закреплены материалом связки, и при образовании наружного слоя разновысотность зерен одинакового размера dcp определится статикой распределения их центров симметрии (тяжести). Рассеивание положений центров зерен предопределяет основную долю дисперсии вершин зерен, выступающих над связкой.
Итак, разноразмерность зерен не существенно искажает параболический характер распределения вершин зерен и для статической модели их распределение может быть принято таким же, как и для центров зерен. Сделанный вывод может быть обоснован и с другой точки зрения. Если имеется «пересечение» двух законов распределения случайной величины, из которых один является симметричным по отношению к распределению другого, то закон распределения последнего не изменяется, увеличивается только дисперсия этого распределения.
Если при переходе от центров симметрии (центров шара dc„) к вершинам зерен в идеальной модели дисперсия равна нулю и вершины зерен распределяются точно так же, как их центры, т. е. по уравнению (1.28), то в реальном инструменте параболическим законом описывается математическое ожидание положения вершин, дополнительно к которому должно быть задано еще среднее квадратическое отклонение вершин зерен по отношению к точке, отстоящей от центра симметрии на расстоянии Rcp ~ Dcр/2.
Таким образом, положение вершин зерен в реальном инструменте должно оцениваться исходя из двух предпосылок: 1) при общем вероятностном анализе строения слоя в качестве характеристики положения вершин зерен должно приниматься распределение их математического ожидания, т. е. распределение точек, отстоящих от центров зерен на величину Rcp, которое подчиняется закону параболы (1.28);
2) в каждом отдельном случае из-за дисперсии распределения вершин формула (1.28) не применима, требуется ее корректировка или определение распределения вершин зерен непосредственно экспериментальным путем.
Все это имеет немаловажное методологическое значение. Ряд исследователей на базе ограниченного числа измерений, проведенных на одном или нескольких абразивных кругах, не могут установить общую статистическую закономерность распределения зерен в ПС инструмента, получая частные зависимости, искаженные дисперсией распределения вершин зерен.
В табл. 7 по данным работы [57] приведены исключающие друг друга закономерности распределения вершин зерен в абразивных кругах, установленные различными исследователями. Такому разнообразию в оценке закономерностей распределения зерен способствовали следующие обстоятельства.
|
Результаты измерений частотного распределения режущих кромок абразивных зерен в направлении по радиусу шлифовального круга по данным различных исследователей
• h — приблизительная глубина от поверхности исследуемого шлифовального круга. |
Измерение числа режущих кромок (выступающих над связкой вершин зерен) осуществляется после вскрытия круга, шлифования или правки. Во всех этих случаях перед опытом производилось силовое воздействие на зерна круга, в результате чего измерялось не естественное распределение вершин зерен, изначально заложенных в матрицу инструмента, а распределение притупленных, сколотых вершин, таящих в себе технологическую наследственность предыдущей обработки. Таким образом, общая картина распределения зерен подменялась частным случаем распределения их сколотых вершин. Кроме того, численно плотность замеренных зерен из — за выпадания зерен и притупления вершин также не совпадала с ожидаемой, исчисленной из концентрации зерен, заложенных в матрицу инструмента.
Таким образом, для выяснения закономерностей распределения зерен в ПС необходимо исходить, как было показано, из теоретических соображений, а экспериментальную проверку полученных выводов производить по методике, исключающей влияние скалывания вершин и выкрашивания самих зерен. Наиболее правильным в методическом отношении являлось проведение такого эксперимента, в котором закон распределения зерен в ПС инструмента был бы однозначно связан с характером распределения других параметров процесса шлифования, надежно фиксируемых в опытах, например сил резания или размеров стружек.
В аспекте рассматриваемого вопроса следует остановиться на влиянии явления несовпадения геометрического центра круга с осью его вращения, возникающего при установке инструмента на станок. Этот вопрос возникает в связи с изменением базы
отсчета в результате вращения круга вокруг некоторой оси. Рассмотрим наиболее простой случай, когда положение оси неизменно в пространстве, т. е. биения оси равны нулю. Тогда в связи с несовпадением расположения ПС с поверхностью цилиндра вращения и необходимостью кинематического переноса каждого зерна на траектории, эквидистантные к нему (что равносильно переносу на окружности, концентричные к оси вращения), возникает необходимость корректировки расположения зерен по отношению друг к другу в
соответствии с траекториями движения их вершин.
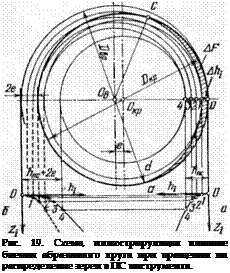
Рассмотрим рис. 19, на котором изображен круг диаметром DKp- Его центр не совпадает с осью вращения Ов на величину эксцентриситета е. В результате вращения все точки круга по отношению к поверхности цилиндра вращения с диаметром DBp = DKp + + 2е смещаются за один оборот на максимальную величину, равную 2е. По отношению к новой базе отсчета — к поверхности вращения, касательной к наиболее выступающему зерну в точке максимального биения, глубина ПС увеличится и станет равной /іПсв= = йпс + 2е; число зерен в слое останется неизменным и равным Zпс-
На рис. 19, а изображена исходная парабола, у которой Znс = = ahne, а на рис. 19, б — парабола, у которой Znc = (hue + + 2е)2. Докажем сперва, что в результате биения поверхности идеального цилиндра — круга по отношению к оси вращения, не имеющей биений, закон распределения зерен в образовавшемся кинематически ПС сохраняется прежним.
Если начальную глубину слоя hue разделить на дифференциально малые слои А/г, (между точками 0—4, рис. 19, й), то вместо суммирования зерен во всем кольце круга между точками 0—1 при вращении суммируются зерна в заштрихованном сегменте с боковой площадью AF на дуге cd.
В связи с тем, что величина hue существенно мала по сравнению с величиной DKt , каждому интервалу Aht соответствуют равные площади AF. Таким образом, число зерен в равных сегментах cd будет нарастать так же, как нарастает число зерен в кольцах между точками 0—1, 1—2, 2—3, 3—4 и т. д., т. е. по закону квадратическом параболы.
Тогда в интервалах 0—1—2—3—4 (рис. 19, б) необходимо откладывать меньшее число зерен, соответствующее отношению площади сегмента AF к площади соответствующего кольца, таким образом, чтобы общее число зерен в слое было одним и тем же при разных глубинах h, = hnc и h. = hnc + 2е. В итоге получим уравнения парабол Znc = айпс и Znc = о, (Zinc + 2е)а. Приравняем ahfjC =
‘
4v
ли Лпс = dcp и а = — . Тогда
Итак, величина а — параметр уравнения параболы — уменьшилась на величину
(1.47,
Оценим допустимую величину биения, которая бы изменяла параметр а не более чем на 5% при С *=* 1,05. Подставим С в (1.47), откуда
(1-48)
Таким образом, допустимая величина биений при измерениях зависит от крупности зерен, составляя постоянную часть его размера. Так, для зернистости 630/500 dC|, = 0,714 ммие« 0,036 мм, а для зернистости 250/200 dq, = 0,304 мм и е~ 0,015 мм. Для мелкозернистых кругов dCp <; 0,132 мм и е < 0,007 мм.
Если учесть биение самой оси вращения и некруглость круга, то при экспериментальном определении распределения зерен в слое с 5%-ной погрешностью необходимо выдерживать радиальное биение измеряемого круга с точностью в несколько микрометров.
Необходимо ли выдерживать столь высокую точность при практическом шлифовании? Ответ не может быть однозначным. Если биения вызывают вибрации и повышение шероховатости, то указанная величина биений должна выдерживаться. При предварительном шлифовании и при жесткой системе СПИД допустимые величины биения могут быть большими, в результате уменьшится число зерен в рабочем слое и на площади мгновенного контакта. При этом уменьшается суммарная сила на круге и снижается температура шлифования, улучшаются условия резания благодаря увеличению площади среза, приходящейся на каждое зерно. Иными словами, явление биения круга может служить в известных пределах одним из средств регулирования распределения зерен в созданном кинематикой движения рабочем ПС инструмента.
Выше был рассмотрен наиболее простой случай отклонений расположения точек круга от идеальной поверхности вращения.
Практически встречаются несколько одновременно действующих факторов: отклонение формы круга от идеального цилиндра, несовпадение геометрической оси круга с осью вращения, биение самой оси вращения, вибрации круга и детали. Складываясь геометрически, все эти отклонения приводят к кинематическому распределению вершин зерен, отличному от квадратичной параболы.
Таким образом, в реальном инструменте, в отличие от его идеальной модели, действуют факторы, которые можно подразделить на две группы. Первая группа факторов, вызывающих скол и износ вершин (шлифование, вскрытие круга и правка), приводит к увеличению плотности вершин зерен в слое. Вторая группа (биение осей вращения, отклонение тела круга от идеальной формы, вибрации), наоборот, уменьшает эту плотность. В итоге суммарного воздействия всех факторов действительное распределение вершин зерен существенно отличается от идеальной параболы, полученной на статической модели круга.
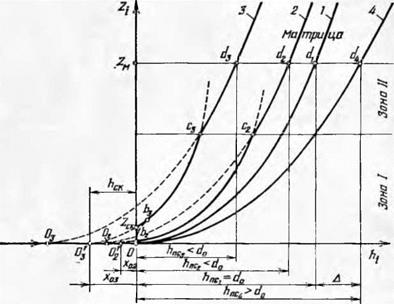
На рис. 20 показаны типичные кривые распределения вершин зерен в поверхностном слое реальных инструментов. Здесь кривая 1 — распределение центров тяжести зерен в инструменте. В статическом состоянии оно близко к распределению центров тяжести зерен в идеальной модели. Кривые 2—4 относятся к рабочему слою реальных инструментов, образованному в процессе вращения круга. При этом кривые 2, 3 отражают факторы, вызывающие скалывание и пришлифовку вершин. На некоторой глубине hCK кривые имеют или «вертикальный» скачок числа зерен ZCK в связи с нахождением вершин на одном уровне, или переходную кривую, связанную с разновысотностью сколотых вершин.
В результате внешнего силового воздействия, вызвавшего скол вершин, распределение их по кривой 2 на участке bfa и по кривой 3 на участке Ь3с3 будет описываться уравнениями, отличными от исходной параболы статической модели. Забегая несколько вперед, отметим, что в случае умеренного износа вершин зерен эти кривые с погрешностью 10—15% удается аппроксимировать параболой общего вида у = ах2 + Ьх 4- с и некоторыми другими кривыми, например степенным уравнением у = ахп.
Кривая 4 на рис. 20 иллюстрирует распределение вершин зерен во вращающемся круге, имеющем биение (при этом износ вершин зерен исключен). Здесь плотность меньше, чем в статической модели, так как at <. at в соответствии с уравнением (1.46).
Таким образом, в реальном шлифовальном круге ПС разбивается на две зоны. Зона / связана с областью воздействия сил шлифования, обрабатываемого материала и стружки, среды (СОЖ и шлама) на вершины зерен, в результате чего положение вершин зерен не остается неизменным. Физически эта зона равна величине выступления зерен над связкой инструмента или меньше ее. Зона II лежит под уровнем связки. Здесь зерна защищены от воздействия внешней среды и распределение их подчиняется законам, установленным на статической модели.
Совершенно очевидно, что на данном этапе статическая модель, основанная на использовании закономерностей распределения зерен в матрице, а именно закона равномерной плотности и закона Пуассона, стала для исследователей недостаточной. В зоне I наряду с этими законами (по-прежнему справедливыми для распределения
|
Рис. 20. Гипотетические кривые распределения зерен по глубине ПС во вращающемся инструменте при силовом воздействии на вершины зерен |
центров зерен) действуют иные законы, связанные не только с геометрической формой и взаимным пространственным положением абразивных частиц, но и с характером разрушения и износа вершин кристаллических зерен, явлением разрушения и вырывания самих зерен из связки, т. е. с динамикой износа ПС (зерна + связка) шлифовальных инструментов в целом.
В настоящее время не представляется возможным чисто теоретическим путем описать закономерности распределения вершин зерен, выступающих над уровнем связки и подвергающихся внешнему силовому и температурному воздействию в процессе эксплуатации шлифовальных инструментов. В связи с этим исследователи используют экспериментально-теоретический путь решения задачи, основанный на опытном определении рельефа ПС абразивного инструмента и описании его с помощью определенных вероятностных моделей. Отметим, что для выяснения распределения зерен на поверхности инструмента не имеется возможности исследовать весь ПС, который в зоне II большей частью скрыт связкой.
На рис. 21 представлены две кривые 1 и 2, отображающие характер нарастания числа зерен по глубине ПС для двух зернистостей, характеризуемых средними эквивалентными размерами зерен d01 и d02, причем d„? >■ dot. При одной концентрации кривая 2 будет расположена правее кривой /, так как для одной глубины частиц с размерами d01 в слое больше, чем частиц с размерами dai.
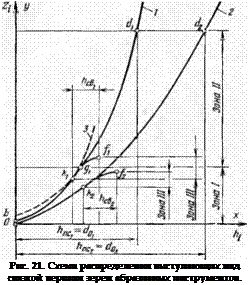Для кривой 1 показано также явление притупления (отрезок ОЬ) при шлифовании наиболее выступающих зерен до одного уровня, а число вершин зерен определяется положением линии Obkxgyd^ состоящей из пересечения в точке ft, двух параболических кривых, характеризуемых разными уравнениями, не проходящими через начало координат и отражающими пространственный сдвиг вершин зерен, подвергнутых силовому и температурному воздействию у = а,*2 + Ьгх + с,
(кривая 1) и yi = cix2 + + biX + с[ (кривая 3). Кривая 2 отображает случай, когда вершины зерен не подвергались этому воздействию, (у2 = GjX2), поэтому она проходит через начало координат, а ее положение соответствует расчетам, произведенным по уравнениям статической модели.
Точки ft, и *2 соответствуют глубине слоя до верхних точек поверхности связки. Таким образом, до этого уровня ни одна вершина зерна не закрывается материалом связки. Колебание уровня связки происходит на величину /гСЬ| и hCB! и образует еще одну зон1′ ПС — зону III, в которой происходит постепенное и все увеличивающееся закрывание связкой вершин зерен, лежащих в более глубоких слоях. В результате такого закрывания видимое количество вершин будет характеризоваться частью кривой 1 (Obklgfl) и частью кривой 2 (Okofv). После точек /, и /2 видимых зерен на поверхности круга не будет.
Таким образом, фиксируемая в опытах тем или иным методом кривая изменения числа зерен по глубине ПС до точек ft, и ftz отражает закон фактического распределения вершин зерен в слое, а на отрезках ft,/, и — явление экранирования зерен связкой.
С методологической точки зрения такое распределение не может быть описано одним законом, т. е. уравнением единой кривой.
Подбор какого-либо уравнения, описывающего кривые Obk^J и Ok2/2 с необходимой для практики точностью, может быть сделан в отдельном конкретном случае, например для подсчета зерен, выступающих над уровнем связки, но это уравнение не может быть отождествлено с законом распределения зерен в ПС инструмента.
Таким образом, уравнения кривых на участках ОЬку и 0/г2 являются сложной функцией, отражающей влияние нескольких факторов: распределения самих зерен (точнее, центров зерен) дисперсии вершин зерен в связи с колебаниями наружных размеров и рельефной поверхности зерен по отношению к их центрам; добавочного смещения вершин зерен, вызываемого процессами правки и шлифования; биения всего ПС в результате вращения круга.
На участках 6j/, и kj,2 вся эта сложная картина маскируется явлением экранирования зерен связкой. Длина участков кривой bkr и Ok2 определяется верхним уровнем расположения связки, а участков и kj2— глубиной рельефа связки. Так, для керамических связок обычных шлифовальных кругов из ЭБ и КЗ они имеют большую длину. Эта длина тем больше, чем крупнее зерно и пористее связка. В то же время для алмазного инструмента на металлических связках эти участки ограничены.
В процессе эксплуатации шлифовального круга при изменении условий и режимов работы размеры кривых bk jj и 0/z2/2 не остаются ПОСТОЯННЫМИ, изменяются И соотношения ветвей bk{ И kJi, 0k2 и kj2. Таким образом, и с этой позиции оказывается невозможным получение единого аналитического уравнения, описывающего видимое распределение вершин зерен над уровнем связки.
Очевидно, целесообразнее ограничиться отысканием закона распределения вершин зерен на начальной части кривых / и 2, до точек и k2, т. е. до глубины реального внедрения вершин зерен в обрабатываемый материал, и использовать полученные зависимости для практических расчетов.
4 8—331