Статическая модель абразивного круга

Изучив характер распределения частиц в абразивном про­странстве и в наружном слое, полученном из него путем разрыва, можно приступить к описанию свойств модели абразивного круга, рассматривая его как часть такого пространства с конкретными размерами абразивных зерен и их концентрацией в матричной части инструмента.

В этой модели по-прежнему: а) все зерна приведены к среднему размеру dcp и к форме шара; б) в матрице распределение зерен описывается случайным законом с постоянной плотностью вероят­ности; в) в ПС для оценки распределения дополнительно привле­каются параболический закон изменения числа зерен по глубине слоя и закон Пуассона в связи с неравномерностью распределения зерен в малых объемах.

Кроме того, предъявим следующие дополнительные требования к этой модели: геометрическая форма круга должна быть идеальной, не имеющей отклонений по отношению к оси вращения (идеальный цилиндр, конус, кольцо, шар и т. д.); распределение массы абразив­ного вещества в объеме по отношению к осям симметрии инструмента идеальной формы должно быть равномерным.

Изучение основных свойств идеализированной статической модели круга проведем на примере инструмента, импрегнированного порошками природных и синтетических алмазов.

Обратимся к формуле (1.24). Для алмазов имеем Q = 0,88 г, W = 1 см3, у = 3,53 г/см3, тогда

(1.42)

Для алмазного «монолита», из кото­рого мысленно дроблением получают порошок, не несущий внутрен­

них пустот и включений, К„= 1 — Тогда К„ =

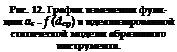
Для решения формулы (1-42) не­обходимо знать величину эквивалент­ного диаметра зерен dcp, которую рас­считаем по экспериментальным дан­ным [16] и формуле (1.23).

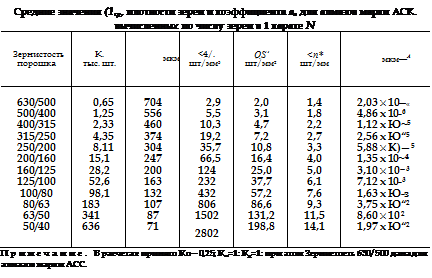
Имея данные для расчета qv в за­висимости от числа зерен в навеске, равной 1 карату для алмазов различ­ных зернистостей, можно рассчитать величины qs, qt, as (по формуле (1.31)) при 100%-ной концентрации алмазов в матрице инструмента. Данные рас­чета приведены в табл. 5.

Отметим, что для К0 = 0,25 (Кп = = 1) и /Сц = 1 имеет место следую­щее равенство: hue = dcp = /м, где /и — среднее расстояние между зер­нами.

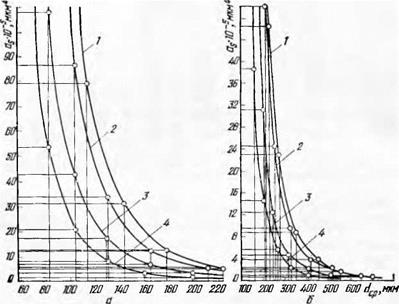
На рис. 12 показана графическая интерпретация зависимости коэффи­циента as = f (dcp), интенсивность ко­торого определяется изменением сред-

них размеров зерен в четвертой степени в соответствии с уравне­нием (1.31).

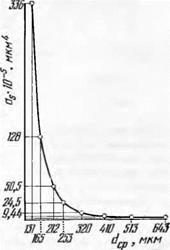
Ряд исследователей в качестве эквивалента используют зерна в виде кубиков, принимая К0 = 0, или шарикоЬ, принимая К0 = = л/6 = 0,524, что приводит к существенным ошибкам. На рис. 13 для этих значений, а также для К0 = 0,2 (для определения «чув­ствительности» величины as к коэффициенту Ко) приводятся кривые

Рис. 13. График изменения функции as— t (dcp) при различных значениях

изменения параметра as в сравнении с кривой, полученной для тео­ретически рассчитанного коэффициента К0 = 0,25. График разбит на два интервала изменения размера dcp, чтобы путем измене­ния масштаба величины as разделить кривые для крупных зернис­тостей.

Данные табл. 5 можно использовать для контроля фактической концентрации зерен в инструменте (например, пользуясь значением поверхностной плотности qs) или при известной концентрации — для контроля заложенной зернистости, для чего удобнее опреде­лять величину средних расстояний между зернами.

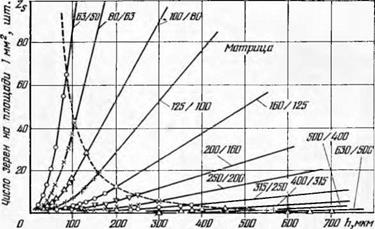
На рис. 14 приводятся формы кривых изменения числа зерен по глубине абразивного слоя для 100%-ной концентрации алмазных порошков различной зернистости.

В соответствии с формулами (1.28) и (1.30) в ПС зерна рас­пределяются по параболической кривой, а начиная с глубины Л, >• hue — по закону прямой линии (1.34).

Граница раздела наружного ПС на рис. 14 условно показана/ штриховой линией.

Угол наклона прямых к оси ht при зернистостях 200/160 и крупнее невелик, в результате чего интенсивность нарастания числа зерен с глубиной слоя на параболической части кривой отклоняется от

Рис. 14. Характер изменения числа зерен по высоте ПС и матрицы аб­разивного инструмента для различных зернистостей алмазного порош­ка (концентрация 100%).

прямой не существенно. Так, до глубины 0,3—0,4 мм для этих зер­нистостей число зерен прирастает в пределах 1—5 шт. на каждый 1 мм2 абразивной поверхности, в результате при экспериментальном определении характера распределения зерен в интервале доступных для изучения глубин (0,005—0,20 мм) большинством исследователей параболический закон распределения зерен не обнаруживается.

Выше для построения модели круга был использован закон статически равномерного распределения зерен в абразивном про­странстве. Используем далее пуассоновский закон распределения. Покажем применимость его для оценки расстояний между зернами.

Пусть прямая при своем движении пронизывает тело абразив­ных зерен. В местах входа и выхода прямой из зерна образуются две точки. Если в качестве расчетной принять среднюю между ними точку, как единственную характеризующую зерно, то измене­ние расстояний между этими точками должно подчиняться распре­делению Пуассона. Для этого имеются все основания. Эти точки распределены в пространстве статически равномерно, точно так же, как абразивные зерна. При своем движении прямая последователь­но пронизывает зерна, так что они не могут одновременно в одном месте появляться парами, тройками и т. д., и появление зерен на прямой происходит независимым образом, т. е. все условия приме­нимости закона І Іуассона соблюдены.

Преобразуем параметр Пуассона а = Я/,. Здесь Я — среднее число точек на единице длины, тогда среднее расстояние, 1 h

между точками 1М — — г-, а а = — у — = г), где г) — отношение текуще-

‘м

Значения вероятности Рт

п	Ртх	Л	РтГ]	•1	Р"Ч і	1)	Р”’ч
0,10	0,00005	1,0	0,3679	3,6	0,0273	7,0	0,0009
0,15	0,0013	1,1	0,3329	3,8	0,0224	7,2	0,0007
0,20	0,0067	1,2	0,3012	4,0	0,0183	7,4	0,0006
0,25	0,0183	1,3	0,2725	4,2	0,0150	7,6	0,0005
0,30	0,0357	1,4	0,2466	4,4	0,0123	7,8	0,0004
0,35	0,0574	1,5	0,2231	4,6	0,0101	8,0	0,0003
0,40	0,0821	1,6	0,2019	4,8	0,0082	8,2	0,00027
0,45	0,1084	1,7	0,1827	5,0	0,0067	8,4	0,00022
0,50	0,1353	1,8	0,1653	5,2	0,0055	8,6	0,00018
0,55	0,1623	1,9	0,1496	5,4	0,0045	8,8	0,00015
0,60	0,1889	2,0	0,1353	5,6	0,0037	9,0	0,00012
0,65	0.2147	2,2	0,1108	5.8	0,0030	9,5	0,00007
0,70	0,2397	2,4	0,0907	6,0	0,0025	10,5	0,00005
0,75	0,2636	2,6	0,0743	6,2	0,0020	1	1
0,80	0,2943	2,8	0,0608	6,4	0,0017	1	1
0,85	0,3084	3,0	0,0498	6,6	0,0014	1	1
0,90	0,3292	3,2	0,0408	6,8	0,0011	1	1
0,95	0,3490	3,4	0,0334

Таблица распределения Пуассона

6

го и выбранного нами отрезка /, к величине среднего расстояния между зернами /м. Тогда уравнение Пуассона примет вид

Ря = ^Ге‘Т)- 0-43)

Расстояние между зернами выражает условие того, что на отрезок lt не попадает ни одного зерна, т. е. т = 0. В этом случае уравнение упростится и примет вид

= (1.44)

Анализ уравнения показывает, что оно справедливо при т] >> 1. Этого вполне достаточно для того, чтобы произвести оценку появ­ления расстояний между зернами, превышающими их средние зна­чения, т. е. расстояния для наиболее удаленных зерен.

Нами принята гипотеза, что вероятность появления зерен с расстояниями, в несколько раз большими значения /м, равна вероятности появления зерен с расстояниями, во столько же раз меньшими. значения /м. Это утверждение однозначно условию, что плотность вероятности распределения расстояний между зернами
носит симметричный характер по отношению к среднему расстоя­нию, для которого г] = 1, и выражается в равенстве абсолютных величин прямых и обратных соотношений ординат IJIM. Значения вероятности Рц = f (т)) приведены в табл. 6.

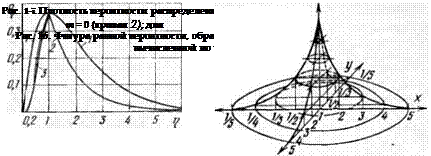На рис. 15 представлены кривые Пуассона по уравнению (1-44) и данным табл. 6 (кривая 2), а также для условий вероятности по­падания одной точки т = 1 на отрезок I, и при условии определе-

ния усредненных расстояний между точками по отношению IJm (со­ответственно кривые 1 и 3). Геометрически интерпретация табл. 6, отражающая условие симметричности вероятностей расстояний ме-

жду зернами относительно сред­него значения /м, отображена на рис. 16, полученном вращением вокруг оси z правой части кри­вой, вычисленной по уравнению (1.44) для ординат т) :1.

На рис. 17 представлена кри­вая распределения относительных расстояний между зернами по уравнению (1.44), на которую на­несены точки т), определенные экспериментально на реальных абразивных инструментах, на ал­мазных правящих роликах, изго­товленных из алмазов А 630/500 методом порошковой металлургии и из синтетических алмазов марки АСК 400/315, изготовленных методом гальванического закрепления алмазов. Расстояния между зернами записывались на ленту самописца с помощью электрического щупа. На ленте запись сигнала щупа при контакте с токопроводимой связ­кой чередовалась с пропусками, когда щуп проходил над зерном. Для надежного контакта с роликом вершины алмазов предварительно
отшлифовывались алмазным кругом до уровня связки. Рис. 17 яв­ляется достаточным подтверждением справедливости выражения •расстояний между зернами по принятой нами методике.

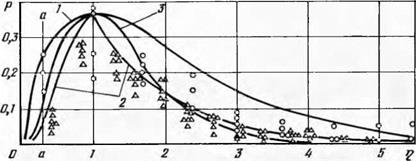
На рис. 18 представлены результаты эксперимента по опреде­лению рассеивания размеров стружек, полученные в работе [51, при шлифовании быстрорежущей стали Р18 кругами типа ЧК из кубического нитрида бора марки КО 125/100-Б1-150% и КР 80/63 на связке МБ2 при скорости шлифования 21 м/с. Глубина шлифова-

Рис. 18. Распределение размеров стружек быстрорежущей стали при шлифовании кругом ЧК из кубического нитрида бора марки КО125/Ю0-Б1-150% и КР80/63 на связке МБ2: I — кривая распределения Пуассона при т = 1; 2 — кривая распределения Пуассона по уравнению (1.44); 3 — кривая, рассчитанная по уравнению (1.45).

ния в опытах была переменной и изменялась в 50 раз (от 0,01 до 0,5 мм/дв. хода). Продольная подача находилась в диапазоне 1— 1,5 м/мин.

Как видно из рис. 18, устанавливается вполне удовлетворитель­ное расположение точек, отображающих рассеивание размеров стружек по ширине (кружки) и толщине (треугольники), по отноше­нию к кривой, полученной по уравнению (1.44). В левой части гра­фика точки тяготеют к ограничивающей прямой а — а как к пре­делу, связанному с физической невозможностью снятия стружек очень малых размеров при данных условиях шлифования. Левая часть кривой рассеивания может быть несколько точнее определена по уравнению, полученному подбором по экспериментальным точкам:

Р„ = бтр9е-2-7£Ч (1.45)

Правая часть кривой 2 уравнения Пуассона может служить мерой рассеивания не только расстояний между зернами, но и размеров стружки. Все это дает возможность прийти к заключению, что и силы, действующие на зерна, подчиняются распределению Пуассона. Таким образом, если известно среднее усилие на одном зерне, то уравнение (1.44) позволяет получить полную картину распределения сил резания на всех зернах инструмента.

Обращаясь к табл. 6, видим, что при 10-кратном превышении переменной расстояний между зернами I, или, в данном случае, переменной силы на зерне Р( по отношению к среднему значению вероятность Pv = 0,0005, т. е. еще имеет значимую величину. Так, на каждые 10 000 зерен 5 из них перегружены в 10 раз сильнее по сравнению со средней расчетной силой на зерне. Ана­логично на каждые 1000 зерен 1—2 зерна испытывают 6—7-кратную перегрузку, а 4—5-кратную испытывают уже 7—18 зерен.

Наибольшую перегрузку испытывают самые верхние зерна ПС, расположенные на больших расстояниях, чем внутренние зер­на, и работающие в качестве прорезных резцов ввиду малой степени экранирования их соседними зернами. Учитывая, что абразивные материалы, обладая высокой твердостью, в то же время имеют не­высокую прочность на удар и легко разрушаются, приходим к за­ключению, что характерным видом износа большинства абразивных инструментов является хрупкое разрушение зерен и вырывание их из связки в связи с наличием (из-за статистики распределения) зерен, усилия на которых превышают их прочность или усилие удер­жания в связке.

В свете сказанного становится понятным утверждение, что не острота вершин и не число острых выступов определяют разницу в стойкости абразивных и алмазных или кубонитовых инструментов. Их влияние на изменение усилия резания не превышает нескольких процентов. Прочные характеристики зерен, прочность удержания в связке, сопротивление силовым и температурным воздействиям предопределяют существующую разницу в работоспособности ин­струментов.

Таким образом, в абразивных инструментах, изготовленных методом спекания (закрепления) порошковых материалов, имеются зерна, которые в момент контакта с обрабатываемым материалом находятся в условиях мгновенного разрушения. Другие зерна в состоянии осуществить лишь несколько актов срезания до разруше­ния, в результате чего идет непрерывное срабатывание абразивного слоя.

Для обновления утраченных режущих зерен необходим запас абразивных зерен, поэтому такие инструменты могут быть только многослойными. Известно, что обычные круги из электрокорунда или карбида кремния даже не имеют корпуса и целиком состоят из матрицы, служащей арсеналом для поставки зерен в режущий слой. У большинства алмазных инструментов имеется также ал­мазоносное кольцо, или слой толщиной в несколько миллиметров, значительно меньших размеров, чем у обычных абразивных ин­струментов в связи с большей прочностью зерен и лучшей степенью их удержания в матрице. Для подобных инструментов не существует режимов, при которых можно было бы избавиться от явления раз­рушения зерен. В самом деле, нагрузка на периферийные зерна оп­ределяется не режимом (например, глубиной резания), а законом распределения вершин ПС и степенью их экранирования друг дру­гом, т. е. строением самого ПС. При любом режиме зерна врежут-.

ся в обрабатываемый материал на глубину, не меньшую глубины перекрытия царапин, образуемых ими на поверхности обработки, в результате чего они получат положенную им перегрузку.

Естественно, при увеличении глубины резания интенсивность износа абразивного инструмента возрастает, но это происходит в связи с увеличением количества зерен, одновременно участвующих в актах срезания обрабатываемого материала, тепловым напряжением на инструменте в целом.

Очевидно, что для уменьшения нагрузок на зерна необходимо изменять само строение абразивного слоя, что и делается для ин­струментов, которые должны обладать весьма высокой износостой­костью. Так, для правящих роликов применяют самые прочные ал­мазы (ювелирного качества) достаточно больших размеров (1—2 мм и более), которые укладывают на поверхности инструмента с оди­наковым шагом, обеспечивая хорошие условия перекрытия, закреп­ляют связкой с хорошей степенью алмазоудержания. Это обуслов­ливает при работе возникновение усилий, значительно меньших критических, вызывающих разрушение кристаллов алмазов или их вырывание. Такие инструменты способны совершать десятки и сотни тысяч актов врезаний без разрушения слоя и кристаллов. Однако они очень дорогостоящие и, главное, не могут обрабатывать большинство материалов, в первую очередь металлы и сплавы, из-за неблагопри­ятной геометрии кристаллов, имеющих плоские вершины, и весьма малой толщины среза (микрометры и их доли).

Таким образом, параболический характер распределения зерен по глубине абразивного слоя является вынужденным, предопреде­ляемым законом равномерной плотности, достижение которой яв­ляется требованием всей технологии изготовления. Такой характер распределения является единственно возможным для осуществления процесса шлифования большинства обрабатываемых материалов. Однако это не значит, что строение наружного слоя нельзя улучшить или изменить в благоприятном направлении.

Возвращаясь вновь к свойствам идеализированного нами абра­зивного пространства и методике образования ПС способом разрыва его ho некоторой плоскости, отметим, что, несмотря на утрату в результате такого акта части зерен, основные выводы остаются в силе. В самом деле, параболический характер распределения зерен в слое определяется статистикой распределения центров зерен в та­ком пространстве, подчиняющейся закону равномерной плотности. Если утрата зерен при разрыве слоя происходит случайным образом, равномерно по всей поверхности образовавшегося слоя, т. е. на ней нет мест с локальным характером потери зерен, то закон равномер­ного распределения не нарушается. Тем более сохраняется в силе закон Пуассона, который, в принципе, не зависит от местной лока­лизации зерен.

При потере части зерен необходимо исходить из изменившейся исходной плотности зерен q’v=a’qv, где а — коэффициент, учитыва­ющий долю утраты зерен в единице объема матрицы.

Таким образом, в реальных абразивных инструментах в про­цессе шлифования из-за выкрашивания в ПС задействовано всегда меньшее количество зерен, чем это следует из расчетной величины концентрации абразива, заложенного в матрицу. Поскольку коли­чество зерен, находящихся под перегрузкой, изменяется в зависимос­ти от режима шлифования, можно прийти к выводу, что не существу­ет шлифовального круга с одной характеристикой — она неодина­кова у одного и того же инструмента при различных режимах шлифования разных обрабатываемых материалов.

Это обстоятельство существенно сужает сферу применимости идеализированных моделей, особенно при конкретных инженер­ных расчетах режимов и параметров процесса шлифования. Од­нако с помощью этой модели можно исследовать принципиальные зависимости и общую закономерность строения абразивных инстру­ментов, а также механизм взаимодействия зерен с обрабатываемым телом.

Помимо переменности числа зерен в слое препятствием исполь­зования теоретической модели для практических расчетов является влияние искажений (износа) формы поверхности самого инструмен­та, биения и вибрации, возникающие при вращении инструмента, отжатая в системе СПИД и др. Чтобы учесть указанные обстоятель­ства, необходимо изучить условия перехода от статической модели к кинематической и динамической.