Абразивное пространство с распределением частиц. по закону Пуассона

Случайная величина X распределяется по закону Пуассона, если вероятность того, что она примет определенное значение т, выражается формулой [26]

= ^ (m = о, 1, 2, 3, …), (1.35)

где а — некоторая положительная величина, называемая пара­метром закона Пуассона; т — случайная величина X, которая может принимать целые положительные значения.

Уравнение Пуассона полностью применимо к абразивному пространству, если под т подразумевать изменение числа абра­зивных зерен. Для закона Пуассона тх = М |Х| = а и Dx — а, т. е. математическое ожидание и дисперсия случайной величины рав­ны параметру уравнения (1.35) а.

Доказано [26], что если имеется линия, плоскость или простран­ство, в которых: точки распределены статистически равномерно со средней плотностью К; точки попадают в неперекрывающиеся облас­ти независимым образом; точки появляются поодиночке, а не пара­ми, тройками и т. д., то число точек т, попадающих на линию и в любую область D (плоскую или пространственную), распределяется по закону Пуассона, при этом параметр а — среднее число точек, попадающих на отрезок линии длиной, равной I, или среднее число точек, попадающих в область D.

Для линии а = hi, для плоскости а = XSd, для объема а — — hVo, где Sd, Vd — площадь и объем области D.

Преобразуем уравнение Пуассона применительно к нашему случаю. Определим вероятность нахождения в единице объема точек (зерен) т, при этом а — hV d = qv X 1. Тогда, принимая во внима­ние (1.25), для объема, равного единице, получаем

объеме степень неравномерности будет меньше ес. н или каких? объемом абразивного пространства необходимо оперировать, чтобы быть уверенным, что степень неравномерности распределения зерен в нем несущественна.

Таким образом, речь идет о таком числе частиц, которое яв­ляется условной границей, разделяющей абразивное пространство с распределением частиц по случайному закону равномерной плот­ности вероятности от абразивного пространства с распределением их по случайному закону, описываемому уравнением Пуассона.

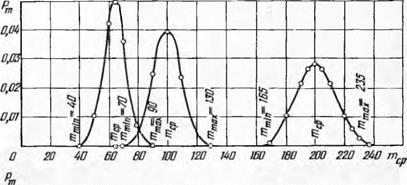
Рис. 9. Изменение формы кривых Пуассона с увеличением параметра а = тср.

Оценим количественно такое число частиц. С этой целью най­дем сперва зависимость Я„,ср = / (тср) (рис. 8). Из рис. 8 следует, что максимальная величина Рт, соответствующая мере тср «= а, с увеличением величины а непрерывно уменьшается, асимптотически приближаясь к оси абсцисс. Характер изменения кривой с достаточ­ной для предварительной оценки точностью описывается зависи­мостью

Р«Ь = 0,3955 (mcp = а)"0-49845. (1.40)

Так, для Рщср = 0,01 значение тср = а = 1600.

На рис. 9 показан характер изменения распределения Пуассона для /Лер, равного 64; 100; 200; 350; 500. Устанавливается, что размах значимых величин mmax и mmin вместе с увеличением тср растет, в результате интенсивность уменьшения величины ес. н, характери­зующей степень неравномерности распределения частиц, существен­
но замедляется. Обработка данных рис. 9 по формуле (1.39) пред­ставлена графически на рис. 10, из которого следует, что характер изменения ес. н = f (/Лер = а) носит асимптотический характер. При значениях тср > 500 кривая изменения величины ес. ц мед­ленно приближается к оси абсцисс.

Для оценки интенсивности изменения величины ес. н < 0,2 вос­пользуемся данными рис. 9 и 10.

Таблица 3

	тср
.0	64	100	200	350	500
тшах	22	93	130	235	395	555
ттт	1	40	70	165	305	445
®С-Н	2.1	0,82	0,6	0,35	0,26	0,22

Значения ес „ ттлх, ттіп

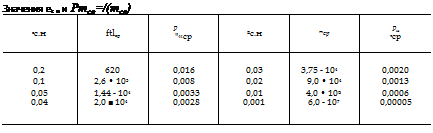
Из (1.39) и рис. 9 получаем значения величины ес. н (табл. 3).

Данные таблицы графически представлены в обычных (рис. 10) и логарифмических (рис. 11) координатах.

Считая что кривая lg єс. н = / (lg mcp) постепенно выполажи — вается, заменяем ее штриховой прямой, тангенс наклона которой равен 0,462. Тогда для значений єс_„ <1 0,22 имеем приближенно

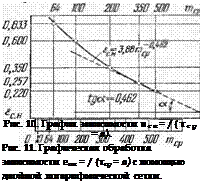єс. н 3,88/л^462. (1.41)

Используя полученное выражение, находим значения тср для ес. н <0,22, а также Рт = f (тср) по формуле (1.40). Данные расчета приведены в табл. 4.

Таким образом, оценивая равномерность распределения зерен величиной єс. н < 0,01, необходимо оперировать объемами, число зерен в которых превышает 4 • Ю5 шт. Очевидно, что когда речь

идет целиком о матрице инструмента, то условно можно считать в ней распределение зерен равномерным, в то время как при оценке числа зерен, «мгновенно» находящихся на площади контакта, необ­ходимо исходить из закона Пуассона.

Для анализа этих величин представляется существенным обя­зательная оценка всего характера распределения в границах изменения числа зерен mmax — /ramin. ,