Абразивное пространство с равномерным распределением частиц

Технология изготовления абразивных инструментов путем дробления и рассева абразивного порошка, смешения его с ком­понентами связки направлена на равномерное распределение частиц в шихте, используемой для прессования и изготовления абразивосодержащей матрицы. Очевидно, можно считать, что для частиц примерно одной формы и размеров, одинаковой плотности при тщательном смешении с помощью, например, «пьяной» бочки, вращающейся в нескольких плоскостях в течение продолжительно­го времени, удается получить однородную шихту, если даже разме­ры и плотность частиц связующего и наполнителей существенно отличаются от абразивного порошка.

Естественно, что равномерность распределения частиц не­правильной формы и отличающихся размерами оценивается здесь со статистических позиций. Для абразивного инструмента со стати­стически равномерным распределением частиц в объеме справедливо выражение

(1.24)

где qv — число абразивных частиц в единице объема, шт./мм3; Q — навеска абразива для получения в объеме концентрации, при­нятой за 100% или за единицу, г; W — объем абразивного слоя,, см*; у — плотность материала абразива, г/см3; /(„ — коэффициент за­полнения объема монолитного вещества абразивными частицами
неправильной формы; dcp — средний эквивалентный диаметр аб­разивной частицы, мм; Кп — коэффициент концентрации, показы­вающий, во сколько раз данная концентрация отлична от принятой за 100% или единицу.

Обозначая К„ = Q/WyK0, получаем

(1.25)

Отсюда, если известна плотность частиц в объеме инструмента, получаем

Формула (1.26) позволяет получить искомый эквивалентный размер частиц, заменяющий собою в среднем все разнообразие размеров реальных абразивных зерен и приводящий неопределен­ную форму к идеальной форме шара. Такая идеализация абразив­ного зерна позволяет существенно упростить создание модели и получить простое соответствие между моделью и инструментом.

Итак, условия соответствия между идеализированной моделью и реальным инструментом следующие: плотность частиц (число частиц) в модели и инструменте должна быть одинаковой; размер частиц dcр модели должен быть получен из условия сохранения числа и массы абразивного вещества в единице объема матрицы; закон распределения частиц в матрице инструмента и модели дол­жен быть принят одинаковым, соответствующим закону стати­стически равномерного распределения частиц в объемах, сущест­венно превышающих по размерам сами частицы; размеры и форма модели и инструмента должны совпадать.

При переходе от реального инструмента к модели не учиты­ваются разноразмерность зерен и различие форм, которые заменяют­ся их эквивалентом — режущим шаром, наделяемым условно этими утраченными свойствами частиц.

Если считать, что размеры частиц подчиняются симметрич­ному случайному закону распределения (например, нормальному закону), то, с одной стороны, величина drp выступает в качестве математического ожидания размеров таких частиц, с другой сторо­ны, если существует симметричный закон распределения изменений формы через приведенный радиус кривизны кривых, отображаю­щих эту форму, то она выступает одновременно в качестве средней меры таких радиусов.

Следующим этапом идеализации является создание модели абразивного пространства как выражения наиболее общих свойств матрицы абразивного инструмента. Под абразивным пространством следует понимать пространство неограниченных размеров, в кото­ром статистически равномерно с заданной плотностью распределе­ны частицы с размерами dcp. Абразивное пространство имеет следующие свойства: число частиц стремится к бесконечности,
т. е. выполняется закон больших чисел; плотность частиц в любой части пространства постоянна (qv = const); объем пространства, приходящийся на одну частицу, постоянен (1 lqv = const); для любой части такого пространства справедливо равенство N( = V, qv (Nt — число частиц; Vt — текущий объем пространства); частицы в пространстве неподвижны и зафиксированы средой, которая отож­дествляется с самим пространством; свойства пространства изо­тропны.

Пространство, состоящее из частиц одинакового размера, в ряде случаев удобно рассматривать как пространство точек, заменяющих собой эти частицы. В качестве точки, заменяющей частицу, может быть принята любая точка, находящаяся на поверхности или внутри шара размером dcp. Удобнее всего принимать за исходную точку центр тяжести или симметрии абразивного зерна или наиболее выступающую точку (вершину зерна).

Введение зерна с эквивалентным и одинаковым размером dcp также удобно, так как позволяет по закону распределения един­ственных точек, выбранных на зерне, судить о законе распределения самих зерен.

Отметим, что абразивное точечное пространство, точнее точки, в нем расположенные, обладают свойством статистической сим­метрии. В самом деле, по отношению к плоскости, проведенной в нем (в общем случае поверхности, эквидистантной к рабочей поверхности инструмента), все точки можно разбить на пары, распо­ложенные по отношению к ней на одинаковом, но противоположно направленном расстоянии. Статистическая симметрия не требует обязательного условия зеркального расположения таких пар, впол­не достаточно, что для каждой точки, расположенной с одной сто­роны плоскости, обязательно найдется другая точка, расположен­ная с другой стороны на таком же расстоянии. В таком случае можно также утверждать, что расположение центров тяжести (симметрии) реальных абразивных частиц, равномерно распределенных в аб­разивном объеме, подчиняется этому закону, если число частиц доста­точно велико.

Рассмотрим далее закономерность изменения числа частиц с изменением объема абразивного пространства. Для этого мысленно, не разделяя пространства, выделим из него параллелепипед с по­стоянным основанием, равным единице площади, и переменной дли­ной X, изменяющейся в пределах от О до х. Тогда число частиц в объеме параллелепипеда будет изменяться вместе с изменением ве­личины X (частицы вне объема параллелепипеда не рассматривают­ся). Рассматривая величину X как случайную и распределенную по закону равномерной плотности на участке (О, х), получаем плот­ность распределения

/(*) =

( С при 0 < X < х;

0 при X < 0 и X > х.

Функция распределения

F (х) = j / (х) dx = С j dx = Сх,

где С — постоянная плотности частиц в объеме параллелепипеда длиной, равной единице, С = qv.

Нарастание числа частиц в выделенном объеме (длиной х) про­исходит пропорционально увеличению размеров этого объема. Иными словами, число частиц по глубине абразивного пространства изменяется по линейному закону. Сохраняется ли эта закономер­ность при образовании поверхности раздела в абразивном простран­стве, т. е. образовавшемся наружном слое? Для выяс­нения этого вопроса необ­ходимо абразивное про­странство расчленить по некоторой плоскости на две части и выяснить, как из­менится распределение час­тиц в области раздела.

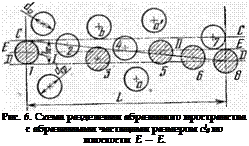
На рис. 6 выделена об­ласть абразивного простран­ства длиной L и шириной В (на чертеже не показана), непосредственно примыкающая к плос­кости раздела Е — Е. Плоскость Е — Е пересекает зерна 1—6 и касается периферии зерен 7—8. Остальные зерна в область разде­ла не попадают и остаются на прежних местах в матрице (напри­мер, зерна а, а’ и Ь).

По отношению к плоскости раздела Е — Е возникают две части (/ и II) абразивного пространства, обладающие свойством статистической симметрии расположения частиц. Частицы, которые пересекаются плоскостью Е — Е или касаются ее, можно подраз­делить на три группы. Первую группу образуют частицы, центры которых лежат в плоскости раздела, а две другие — частицы, центры которых лежат над и под плоскостью раздела.

В силу изотропности свойств и симметрии расположения зерен по отношению к плоскости раздела при разделении пространства зерна распределяются поровну между верхней и нижней частью абразивного пространства. При этом первая группа частиц разде­лится между ними поровну, а остальные две группы, число зерен которых вследствие статистической симметрии равновелико, отой­дут каждая со своей частью.

Таким образом, при разделе возникает поверхностный слой (ПС) глубиной hnc, ограниченный плоскостями С — С и D — D. В общем случае максимальная глубина такого слоя равна К^1ср — размеру наибольшего по габаритам зерна, который превышает в Ка раз средний приведенный размер dcp, т. е. /гпо = Kddcр. В рассмат­
риваемом случае, когда абразивное пространство заполнено экви­валентными зернами одинакового размера, hue = dcр.

Если теперь рассмотреть наружный слой зерен в одной остав­шейся части, например I, то в нем будет находиться лишь половина зерен, соответствовавших ранее полному слою матрицы между плоскостями С — С и D — D (на рис. 6 эти зерна заштрихованы). Плотность зерен в оставшемся слое не изменится, так как согласно свойствам абразивного пространства объем, приходящийся на одно зерно в нем, величина постоянная как для целого пространства, так и для отдельной его части.

Итак, при разрыве абразивного пространства на две части воз­никает ПС глубиной ЛПс; плотность зерен в слое остается постоян-

Z,

нои, равной плотности частиц материнского пространства = = q = const (Z( —число частиц (зерен) при текущем изменении абразивного объема й?,).

При значительных размерах площади справедливо, что отноше­ние приращения числа зерен к приращению объема выделенного пространства величина постоянная, т. е.

Выражение (1.28) указывает, что при разделении абразивного пространства с равномерной плотностью зерен qv число зерен в образовавшихся двух поверхностных слоях равно друг другу и составляет половину зерен, ранее находившихся в этом слое матрицы.

Формула (1.28) указывает на параболический закон нарастания числа зерен в наружном слое инструмента, т. е. на строгую матема­тическую функцию как меру случайных колебаний местоположения центров зерен, статистически рассеянных в абразивном простран­стве и не лежащих в одной какой-либо избранной плоскости.

Обращаясь к формуле (1.28) и обозначая через а множитель при А?, получаем

2, = аЩ. (1.29)

Для объемов с основанием BL = 1 получим

Zs, = asK], (1.30)

4v

Кп*ц 2dL

где as — 2^

В свою очередь среднее расстояние между абразивными частицами равно

Из формулы (1.32) следует, что глубина ПС, которую в даль­нейшем будем обозначать dcp = Апс, и среднее расстояние между зернами соизмеримы со средним размером абразивных зерен и не­существенно зависят от концентрации их в объеме матрицы.

Определим угловой коэффициент гк касательной к кривой, описываемой уравнением (1.30) в точке ht = Апс-’

= = 2а>с = %■ (1-33)

Таким образом, по отношению к рассматриваемой точке, лежащей на разделе наружного ПС и абразивной матрицы, имеет место пара­болический закон нарастания зерен до глубины h{ = Апси линейный закон нарастания зерен при h( > Апс в матрице, характеризуемый выражением

ZM, = qvht. (1.34)

Итак, используя модель абразивного пространства, из которого путем разрыва был образован ПС, удалось установить параболи­ческий характер нарастания числа зерен по глубине этого слоя.

С математической точки зрения ограниченные абразивные пространства, которые являются подпространствами более общего абразивного пространства и внутри которых действует случайный закон равномерного распределения зерен, а в наружном слое имеет место строгая математическая функция, следовало бы назвать функ­ционально замкнутыми.

Несмотря на отличие законов распределения частиц в наружном слое и внутри ограниченного абразивного пространства (матрицы модели), остается неизменным условие постоянства плотности час­тиц в объеме, поскольку каждая удаляемая при разрыве частица «уносит» по условию (1 !qv = const) с собою причитающуюся ей часть объема пространства. Эти утверждения справедливы и для зерен, оставшихся в только что сформированном ПС инструмента.

Таким образом, можно утверждать, что распределение цен­тров абразивных зерен у абразивного инструмента в процессе эксплуатации остается неизменным (упругими или пластическими деформациями, возникающими в результате силового и температур­ного воздействия пренебрегаем), оно задается технологией изго­товления порошковых материалов и не меняется в дальнейшем при износе и правке инструмента.

Полезным будет следующее сравнение. Абразивный инструмент можно представить как жесткую решетку, в углах которой за­креплены зерна. Снаружи решетка разорвана и зерна с одной сторо­ны оголены, не имеют связей. При разрыве решетки часть зерен ут­рачена, в результате чего образовался ПС. В процессе эксплуатации происходит постепенное разрушение наружных частей решетки, в результате ПС сдвигается внутрь системы.

Таким образом, абразивный инструмент имеет две части: 1) матрицу — статически неподвижную систему жестко связанных частиц, «наследницу» метода ее изготовления, представляющую арсенал (запас) абразивного вещества; 2) ПС — динамически под­вижную и непрерывно изменяющуюся под воздействием обрабаты­ваемого материала или правящего инструмента систему абразивных частиц, местоположение которой непрерывно (равномерно или скач­ками) смещается внутрь матрицы.

Априори нами при создании абразивного пространства и сфор­мированной из него модели абразивного инструмента была принята гипотеза о равномерном распределении частиц в объемах, существен­но превышающих объем этих абразивных частиц. Это положение равнозначно утверждению, что, начиная с некоторого числа частиц, неравномерностью их распределения, связанной со случайным, вероятностным характером распределений частиц, можно пренебречь.

Оценку степени неравномерности распределения частиц в ог­раниченных объемах удобнее произвести с помощью модели, в которой они распределены по закону Пуассона.