ВИХІДНІ ПОКАЗНИКИ ШЛІФУВАННЯ. ЗА ПРУЖНОЮ СХЕМОЮ З ЕЛЕКТРОЕРОЗІЙНИМИ. КЕРУЮЧИМИ ДІЯМИ НА РПК

6Л Обґрунтування способу стабілізації вихідних технологічних
показників шліфування за пружною схемою

Відомі різні шляхи реалізації шліфування за пружною схемою, які різ­няться параметром, що підтримується постійним під час оброблення. До таких параметрів відносяться:

а) радіальна сила Ру [84];

б) тангенціальна сила Р2 [85, 86];

Вибір способу стабілізації вихідних технологічних показників необхідно, на нашу думку, здійснювати з урахуванням забезпечення виконання ряду кри­теріїв:

— відсутність фазово-структурних змін у поверхневому шарі заготовки під час обробки при зміні різальної здатності круга;

— простота конструктивної реалізації;

— забезпечення прийнятної продуктивності процесу обробки та ін.

Порівняння вказаних способів стабілізації вихідних показників шліфу­вання виконаємо, використавши математичну модель процесу різання за пруж­ною схемою.

При шліфуванні за пружною схемою з підтримкою постійної радіальної сили підтиску заготовки до шліфувального круга Р„ = Ру (див. рис. 2.9) втрата згодом різальної здатності РПК проявляється через зміну глибини шліфування. Таким чином, еволюція підсистеми різання в часі в результаті погіршення різа­льних властивостей РПК при постійному значенні складової Ру однозначно опи­сується зміною в часі фактичної глибини шліфування =/[г).

Математичну модель процесу шліфування за пружною схемою з постій­ною радіальною силою підтиску заготовки до шліфувального круга Р„ розро­бимо для випадку, коли зниження різальної здатності круга викликане тільки зношуванням зерен, використовуючи наступні допущення:

— вплив режимів шліфування на сили різання при обробленні за аналогіч­ними за кінематикою жорсткою та пружною схемами є ідентичним;

— критерієм стабілізації вихідних технологічних показників шліфування є відсутність перевищення температурою поверхні різання критичного значення Ткр, вище якого відбуваються фазово-структурні зміни в поверхневому шарі об­роблюваного матеріалу;

— процес теплообміну в зоні різання є стаціонарним;

— продуктивність оброблення не залежить від способу шліфування за жо­рсткою або пружною схемами, якщо вона здійснюється кругами ідентичних ха­рактеристик на аналогічних режимах при однакових силах різання.

В силу приведених допущень граничне значення параметра оброблення Р„ = Ру знайдемо, виходячи з критичної температури 7^, яка не повинна пере­вищити при обробленні температуру на поверхні різання. Відомо [79], що мак­симальна температура на поверхні різання пов’язана зі значенням тангенціаль­ної сили Pz співвідношенням

Товщина зрізу аг визначається за формулою (4.26), а максимальна товщи­на комоподібного зрізу послідовно контактуючими зернами а2твх при плоскому шліфуванні розраховується за формулою (3.47).

а кут дії

де у — передній кут кульової моделі зерна;

Кі — коефіцієнт усадки стружки.

Довжина площадки контакту зерна з обробленою поверхнею 4 розрахо­вується за формулою (2.24), а кількість одночасно контактуючих зерен — за фо­рмулою

де В — ширина шліфування,

L — довжина дуги контакту абразивного зерна із заготовкою.

Площа зони контакту заготовки з кругом [54]

S=BdJ5^. (6.9)

Сукупність формул (6.5), (4.26), (3.47), (6.6) — (6.9), (2.24) становить со­бою математичну модель процесу плоского шліфування за пружною схемою, яка відображає еволюцію підсистеми різання в часі, для випадку, коли знижен­ня різальної здатності круга викликане тільки зношуванням зерен, оскільки, бу­дучи вирішеними щодо перемінної іф, ці формули дозволяють визначити закон зміни фактичної глибини шліфування (тобто продуктивності процесу шліфу­вання) у часі обробки.

Рівняння (6.5) аналітично вирішити відносно фактичної глибини шліфу­вання неможливо, тому що воно є трансцендентним, а величина входить у дане рівняння в неявному вигляді в залежностях для визначення максимальної товщини комоподібного зрізу (4.26), кількості одночасно контактуючих зерен (6.8), площі зони контакту заготовки з кругом (6.9) та ін.

У зв’язку з цим представимо умову, яка забезпечує відсутність фазово — структурних перетворень у матеріалі заготовки при обробленні, у вигляді нері­вності

0,987^ <Г< 1,007^. (6.10)

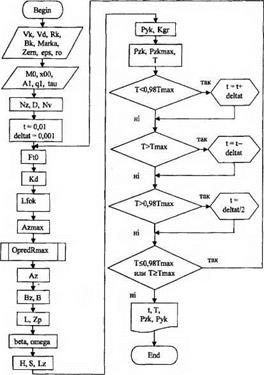
Нерівність (6.10) з урахуванням (6.5) вирішується відносно іф на ПЕОМ покроковим методом з використанням розробленої нами програми (рис. 6.1) за даними про параметри РПК, які сформовані під час правки [87]. Знайдене зна­чення є максимально можливою вихідною глибиною шліфування t0, яка забез­печує відсутність дефектів на поверхні заготовки на початку оброблення.

Використовуючи (о, за формулою (6.4) або за формулою, отриманою під­становкою в (6.4) виразів (6.2) і (6.3), яка має вигляд:

розраховуємо припустиме значення радіальної складової [Ру], яке повинне під­тримуватися постійним за допомогою пружного підтиску заготовки до РПК протягом усього часу оброблення.

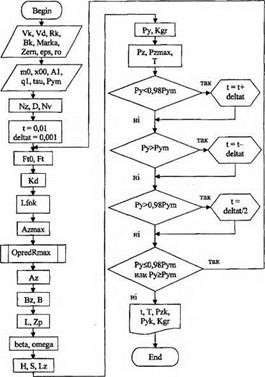
Далі за формулою (6.11) покроковим методом за складеною для цього програмою (рис. 6.2) на ПЭВМ розраховуємо в різні відрізки часу обробки по­точну фактичну глибину шліфування, при якій виконується нерівність

0,98[Ру] <РУ< 1,00[Ру].

Використовуючи дані розрахунку за формулою (6.12), закономірність зміни глибини шліфування іфі у часі оброблення т у результаті процесу зношу­вання зерен опишемо виразом вигляду

Іф(т) = tyc 1 + д*,-ехр(«іт),

Де tycm — стала глибина шліфування, яка встановилася під час оброблення і на­далі практично не змінюється;

<о — вихідна глибина шліфування рельєфом, параметри якого сформовані пі­сля електроерозійної правки круга;

Дґі — to — fycmi — амплітуда зниження глибини шліфування;

ОТ] — емпіричний коефіцієнт.

Сталу глибину шліфування та вихідну глибину шліфування визначимо, використовуючи розрахункові дані, отримані за допомогою математичної мо­делі процесу плоского шліфування за пружною схемою з використанням про­грам для ПЕОМ (див. рис. 6.1, 6.2), а значення коефіцієнта а — обробкою роз­рахункових даних методом найменших квадратів.

Зміну в часі фактичної глибини шліфування ц при обробленні за пруж­ною схемою у випадку спільної дії на різальну здатність РПК процесів засалю-

Рис. 6.1. Блок-схема програми визначення вихідної глибини шліфування to за пружною схемою з постійною силою Ру

Рис. 6.2. Блок-схема програми визначення поточної фактичної глибини шліфування за пружною схемою з постійною силою Ру

вання міжзеренного простору і зношування зерен опишемо рівнянням, аналогі­чним (6.13). У загальному вигляді залежність глибини шліфування від часу об­роблення в цьому випадку може бути представлена в такий спосіб:

= tycm2 + Лг2-ехр(а2г), (6.14)

де величини мають той же фізичний зміст, що й у рівнянні (6.13).

Параметри рівняння (6.14), яке відображає спільну дію на фактичну гли­бину шліфування процесів засалювання міжзеренного простору та зношування зерен, визначаються експериментальним шляхом і наведені в нашій роботі [88].

Для того щоб залежність (6.14) можна було використовувати не тільки з початку координат, де т = 0, а і з будь-якого іншого моменту часу, коли по­чнеться зміна різальної здатності круга у результаті спільної дії процесів заса­лювання міжзеренного простору РІЖ та зношування зерен, переведемо її в без­розмірний вигляд, поділивши рівняння (6.14) на величину t0:

f^ = W+A?2exp(«2r).

f0 *0 *0

У результаті одержимо рівняння для безрозмірної поточної фактичної глибини шліфування? ф2:

Їф2 = V„2 + Д*2′ ехр(а2г), (6.15)

де tycm2 — безрозмірна стала глибина шліфування;

At2 = 1 — tycm2 — безрозмірна амплітуда зниження глибини шліфування вна­слідок зниження різальної здатності круга.

Виконаємо дослідження зміни в часі поточної фактичної глибини шліфу­вання іф при обробленні за пружною схемою з постійною радіальною силою Ру (див. рис. 2.9).

Значення фактичної глибини шліфування в різні періоди оброблення, а також значення параметрів Р„ Ру, Кш і Ту процесі шліфування за пружною схе­мою розрахуємо для випадку, коли зниження різальної здатності круга викли­кане зношуванням зерен.

Розрахунки виконаємо для умов плоского врізного шліфування швидко­різальної сталі Р6М5ФЗ кругом 1А1 250x76x15x5 АС6-100/80-4-М2-01. Пара­метри зерен: діаметр кульової моделі d = 132 мкм, кут загострення є=91°, раді­ус округлення вершини р = 6,69 мкм для моделі у вигляді конуса з округленою вершиною; параметри розподілу різновисотності зерен після електроерозійної правки, який описується законом Вейбулла: m = 2,23, х0 = 2946. Режими оброб­лення: VK = 35 м/с, Vi = 6 м/хв. Фізико-механічні властивості стали Р6М5ФЗ:
коефіцієнт температуропровідності а = 4,1-10"® м2/с, коефіцієнт теплопровідно­сті Я = 19,5 Вт/м-К, критичне значення температури, вище якої відбуваються фазово-структурні перетворення в оброблюваному матеріалі 7^ = 815 К.

Припустиме значення радіальної сили становило [Ру] = 80 Н при макси­мальній розрахованій температурі на поверхні різання Т = 813 К, яка гарантує відсутність фазово-структурних перетворень у поверхневому шарі заготовки.

Отримана в результаті розрахунків закономірність зміни фактичної гли­бини шліфування під час оброблення характеризує вплив на різальну здатність круга тільки процесу зношування зерен.

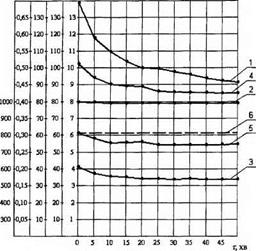
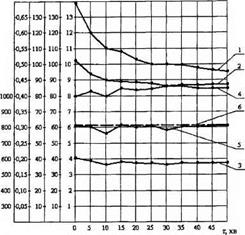
Результати розрахунків (рис. 6.3), дозволяють зробити наступні висновки:

— із збільшенням часу оброблення поточна фактична глибина різання зменшується (крива 1);

— температура на поверхні різання в будь-який момент часу оброблення не перевищує критичного значення Ткр (крива 5).

Якщо зменшення їф зі збільшенням часу оброблення прогнозувалося і по­яснюється погіршенням різальної здатності РПК за рахунок утворення площа­док контакту на задніх поверхнях зерен, а також за рахунок збільшення кілько­сті контактуючих зерен унаслідок зменшення їх різновисотності (що приводить до зменшення коефіцієнта шліфування (крива 4 на рис. 6.4)), то на аналізі при­чин закономірності зміни температури на поверхні різання (крива 5) зупинимо­ся більш докладно.

Для цього проаналізуємо формулу для розрахунку температури на повер­хні різання (6.1). З формули витікає, що температура залежить від величини тангенціальної складової Р„ а також від глибини шліфування, яка впливає на умови теплообміну через площу зони контакту S (формула (6.9)) і безрозмірну напівширину джерела тепла Я, яка визначається за формулою [89]

2а-

Оскільки зі збільшенням гпри шліфуванні з постійною Ру (крива 2) скла­дова Рг зменшується (крива 3), то кількість тепла, що виділилося, теж зменшу­ється, що буде сприяти пропорційному зниженню температури на поверхні рі­зання Т. Зменшення безрозмірної напівширини джерела тепла Я також викличе зменшення температури Т у фф разів. І, навпаки, тільки зменшення S у разів буде сприяти збільшенню Т.

У результаті сумарної дії цих факторів на температуру та переважного впливу параметрів Pz і Я температура на поверхні різання зі збільшенням часу оброблення буде знижуватися.

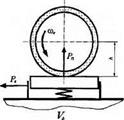
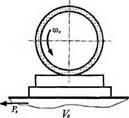
Шліфування з постійною силою Р2 можливо реалізувати за двома схема­ми (рис. 6.4, а, б). За першою схемою (рис. 6.4, а) круг пружно підтискається до заготовки, за другою (рис. 6.4, б) — положення осі круга жорстко зафіксоване

Рис. 6.3. Зміна температури на поверхні різання та параметрів оброблення швидкорізальної сталі Р6М5ФЗ при плоскому врізному алмазному шліфуванні з постійною радіальною силою [PJ = 80 Н 1 — поточна фактична глибина шліфування їф 2 — складова сила різання Ру; 3 — складова сила різання Pz; 4 — коефіцієнт шліфування Кш 5 — температура поверхні різання Т; 6 — температура порогу фазово-структурних перетворень

відносно оброблюваної поверхні. Зміна різальної здатності РПК у процесі об­роблення в першій схемі компенсується зміною величини h, що веде до змен­шення фактичної глибини шліфування fy, у другий — зменшенням подовжньої швидкості столу Vd.

Визначимо закон зміни в часі поточної фактичної глибини шліфування їф при обробленні з постійною тангенціальною силою Р7 за першою схемою.

Припустиме значення параметра обробки Рг установимо, виходячи з тих же умов і допущень, що і припустиме значення радіальної сили Ру. Нерівність

(6.10)

з урахуванням (6.5) вирішимо за програмою, аналогічною представлений на рис. 6.2, для зазначених раніше умов і режимів шліфування. Початкова гли­бина шліфування склала to = 13,88 мкм, припустиме значення тангенціальної складової [Рг] = 40 Н при максимальній розрахованій температурі поверхні рі­зання Т- 813 К.

а б

Рис. 6.4. Схеми оброблення з постійною тангенціальною силою Pz а — Р„ Уй, Рп = const, іф — var, б — Р„ іф — const, Vd, Ру — var

Потім для різних відрізків часу оброблення за програмою, аналогічною представленій на рис. 6.2, розрахуємо поточну фактичну глибину шліфування Гф, при якій виконується нерівність

0,98[PJ <Рг< 1,00[PJ, (6.17)

а також визначимо параметри оброблення Р„ Ру, Кш і Т (рис. 6.5).

Як витікає з приведених даних, фактична глибина шліфування зменшу­ється зі збільшенням часу оброблення якісно аналогічно шліфуванню з постій­ною силою Ру, чого не можна сказати про максимальну температуру на поверх-

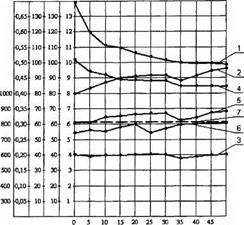
Т, ХВ Рис. 6.5. Зміна температури поверхні різання та параметрів оброблення швидкорізальної сталі Р6М5ФЗ при плоскому врізному алмазному шліфуванні з постійною тангенціальною силою [Рг] = 40 Н 1 — поточна фактична глибина шліфування 2 — складова сила різання Ру 3 — складова сила різання Pz; 4 — коефіцієнт шліфування Кш; 5 — температура на поверхні різання Г; 6 — температура на поверхні різання при шліфуванні з постійною силою Рг, яка визначена за характеристиками рельєфу круга, що стабілізувався; 7 — температура порогу фазово-структурних перетворень

ні різання. Уже після 5 хвилин оброблення її величина починає перевищувати критичну, що призведе до появи фазово-структурних перетворень в обробленій поверхні заготовки, тобто до погіршення її’ якості.

Розглянемо причини виявлених закономірностей.

При обробленні з постійною силою Рг за першою схемою (Vd = const, Іф = var) (див. рис. 6.4, а) зменшення призведе до зменшення температури в фф разів в результаті зменшення безрозмірної напівширини джерела тепла Н у фф разу і зменшення площі контакту S у фф разу. Отже, відповідно до формули (6.1) вплив величини S, яка знаходиться в знаменнику формули, буде переваж­ним, і максимальна температура на поверхні різання буде збільшуватися зі збі­льшенням часу оброблення.

При обробленні за другою схемою (Vd — var, 1Ф = const) (див. рис. 6.4, б) зменшення в часі швидкості столу Vd буде сприяти, з одного боку, збільшенню температури пропорційно зміні Vd, тому що величина Vd у формулі (6.1) знахо­диться в знаменнику. З іншого боку, це приведе до зменшення температури, оскільки безрозмірна напівширина джерела тепла Н, що знаходиться в чисель­нику формули (6.1), зменшиться в разів (див. формулу (6.16)). У результаті переваги безпосереднього впливу Уд на температуру на поверхні різання вона буде зростати.

Розглянемо зміну показників шліфування за пружною схемою у випадку, коли в якості параметра керування використовується температура на поверхні різання Т, яка визначає поріг фазово-структурних перетворень (7^ = 815 К), а фактична глибина шліфування зі збільшенням часу оброблення т зменшується ідентично шліфуванню з постійною силою Ру (рис. 6.6).

При цьому складова Pz зі збільшенням часу оброблення має тенденцію до зменшення, а складова Ру — до збільшення. Відповідно до формули (6.1) змен­шення Рг обумовлене зменшенням площі зони контакту заготовки з кругом S внаслідок зниження фактичної глибини шліфування (див. формулу (6.9)).

Порівнюючи розглянуті методи стабілізації вихідних технологічних пока­зників якості оброблення при шліфуванні за пружною схемою, можна зробити наступні висновки:

— методи стабілізації вихідних технологічних показників з використанням параметрів Ру і Т забезпечують необхідну якість за показниками фазово — структурного стану поверхневого шару протягом усього часу оброблення, при цьому керування процесом шліфування по параметру Ру може бути реалізоване конструктивно простіше;

— при використанні в якості параметра керування обробленням постійної складової Pz, величина якої визначена по характеристиках РПК, сформованих під час правки, не забезпечується сталість якості оброблення.

Рис. 6.6. Зміна температури на поверхні різання і параметрів оброблення швидкорізальної сталі Р6М5ФЗ при плоскому врізному алмазному шліфуванні з постійною температурою Т= 815 К 1 — поточна фактична глибина шліфування іф 2 — складова сила різання Ру; 3 — складова сила різання Рг; 4 — коефіцієнт шліфування Кш; 5 ~ температура на поверхні різання Т; 6 — температура порогу фазово-структурних перетворень

Відзначений недолік керування процесом за допомогою параметра Р7 мо­жна усунути, визначаючи значення Рг за характеристиками РПК у період їх ста­білізації (після 15-30 хв оброблення).

У підтвердження сказаному з використанням нерівності (6.10) і формули

(6.5) за методикою, аналогічною використаним раніше, визначимо припустиме значення тангенціальної складової [Рг] = 37 Н за параметрами рельєфу, сфор­мованими після 20 хвилин оброблення. При цьому максимальна розрахункова температура поверхні різання дорівнює Т= 800 К.

Розраховану для цього значення Р2 поточну фактичну глибину шліфуван­ня, яка задовольняє нерівності (6.17) у різні моменти часу оброблення, викорис­товували для визначення максимальної температури поверхні різання на заго­товці (крива 6 на рис. 6.5). Відповідно до отриманого графіка, максимальна те­мпература в будь-який момент часу не перевищує її критичного значення. Од­нак у цьому випадку вихідне значення фактичної глибини шліфування t0 — 13,25 мкм трохи менше, ніж при керуванні процесом за допомогою параметрів Ру іТ (у цих випадках t0 = 13,88 мкм), що призведе до зниження продуктивності шліфування.

Таким чином, для подальших досліджень показників оброблення за пру­жною схемою приймаємо спосіб стабілізації вихідних технологічних показни­ків процесу шліфування з підтримкою постійною радіальної складової сили рі­зання Ру.