Міцність закріплення алмазного зерна в металевій зв’язці

Розрахунок міцності закріплення в металевій зв’язці алмазного зерна, на­вантаженого зосередженою силою, яка проходить через центр зерна, виконаємо при наступних вхідних положеннях:

— зерно заміняється просторовою моделлю у вигляді абсолютно жорсткої

кулі;

— зв’язка представляє однорідний, ізотропний пружно-пластичний півпро-

стір;

— фізико-механічні властивості зв’язки не залежать від величини пластич­ної деформації;

— на закріплення зерна не впливають розташовані поруч зерна;

— течія зв’язки по поверхні зерна відсутня через шорсткість його поверхні.

Відповідно до технології виготовлення алмазного інструмента на метале­вій зв’язці закріплення зерен здійснюється в процесі допресування алмазовміс — ного шару. Оскільки хімічна взаємодія на межі «зерно-звязка» для марки М2-01 практично відсутня, а фізична взаємодія на рівні сил Ван-дер-Ваальса не має істотного впливу на характер закріплення алмазних зерен [80], то можливо припустити, що закріплення зерна в зв’язці досягається за рахунок механічного защемлення.

Виходячи з вищесказаного, порушення закріплення зерен відбувається в результаті пластичної деформації зв’язки, що приводить до порушення контакту на межі «зерно-звязка», тобто до утворення пустот. При цьому зерно може ви­пасти зі зв’язки, або утримуватися в ній. Однак у результаті можливості пере­міщень у лунці, що утворилася, таке зерно не може виконувати роботу, анало­гічну закріпленому.

Визначимо величину граничного зусилля, яке приводить до порушення закріплення зерна в зв’язці, використовуючи теорію ліній ковзання і методику обчислення питомих сил при впровадженні в матеріал пуансона сферичної фо­рми [81].

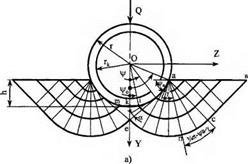
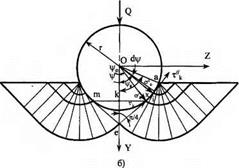
З урахуванням контактного тертя поле ліній ковзання, яке відповідає умо­вам пластичної рівноваги, буде мати вигляд, показаний на рис. 5.3, а.

У області авс поле ліній ковзання утвориться ортогональними прямими, що перетинають зовнішній контур під кутом я/4, тому що межа пластичної об­ласті є прямолінійною і вільною від навантаження. Лінія ас, яка обмежує об-

Рис. 5.3. Поле ліній ковзання при навантаженні кульової моделі зерна а — 0 < рі < 0,5; б — /х, = 0,5

ласть авс, є прямою, тому одне із сімейств ліній ковзання в сусідній області та­кож повинно складатись з прямих ліній. Це випливає з того, що кут між дотич­ними до двох ліній ковзання одного сімейства в точках їхнього перетинання з лініями ковзання іншого сімейства залишається постійним на всьому протязі цих ліній. Межею області є пряма an, яка перетинає дотичну до контуру під ку­том у

де Ці — коефіцієнт тертя.

Точка а є особливою і сітка ліній ковзання утворить центроване віяло асп

із кутом — іг — j/a — % величина якого 4

шеннями.

У області eifan одне сімейство ліній ковзання складається з двопарамет — ричного сімейства прямих, які перетинають контур кулі під кутом у, а друге сі­мейство складається з кривих ліній, ортогональних до прямих першого сімейс­тва. Ці лінії ковзання є евольвентами кола радіуса rK — rcos у.

При величині кута ф = р0 прямолінійна характеристика іе перетинає вісь симетрії під кутом 7і/4. Тому з рис. 5.3 будемо мати = 7г/4 — у, а з урахуванням (5.30)

Область ткіе є областю пластичної рівноваги, яка рухається разом із зер­ном як жорстке тіло.

Як випливає з формули (5.30) при у = 0 тертя на поверхні зерна досягає найбільшої величини, обмеженої умовою пластичності тв = к, де к — пластична постійна, Н/мм2. Цій величині відповідає за формулою (5.30) найбільше зна­чення коефіцієнта тертя Ді= 0,5 (рис. 5.3, б).

Величина зусилля, яке діє на зерно, визначається інтегралом від нормаль­ної і дотичної компонент, узятих по поверхні контакту.

Уздовж твірної еі величини дотичної і нормальної компонент напруження постійні:

Величину зусилля Q’, яке діє на конус, утворений обертанням твірної еі навколо осі OY, знайдемо, помноживши площу бічної поверхні конуса на прое­кції нормальної і дотичної компонент напруження на вісь OY.

Площа бічної поверхні конуса еіт

Після відповідних підстановок

Проекції нормальної і тангенціальної компонент напруження на вісь OY, ,71, . П

<їну=<гп cos-; Туу =rKsm—.

Тоді з урахуванням (5.32)

<2′ = 3б(г1у -<г’иу) = W S1^°[ksinj + 2k(0o-y/0)cos^1 =

sin- L 4 4J (5.34)

4

= sin2 y0 (0,5 + 60-y/0).

Зусилля, яке діє на елемент поверхні кульового пояса, утвореного обер­танням дуги іа навколо осі OY, знайдемо, помноживши площу поверхні елемен­та кульового пояса, обмеженого кутом dp, на суму проекцій дотичної і норма­льної компонент на вісь OY.

Величина нормальної і дотичної компонент напруження у точці / куль­ового пояса

т"к = kcos2% а"в = — 2к(в — р),

Проекції цих компонент напруження на вісь OY т"ку = т" sin ф; а = a"ncos ф.

Площа поверхні елемента кульового пояса Я™ = 2ЯУ2 япф Аф.

Тоді зусилля, яке діє на елемент поверхні кульового пояса

dQ" = (т% — а"пу)Б, шп = Ікжг2 [cos 2ysin 2ф + (в — ф) sin 2фЩ. (5.36)

Щоб одержати загальне зусилля, яке діє на кульової пояс, проінтегруємо вираз (5.36) у межах від фс до фа, де фа — кут заглиблення

Після відповідних операцій і перетворень

Q" = 2кта-2[{в — ^Jsin2 у/а — {в — iy0)sin2 v0 + (l + cos2y)x

3. (2^Q-sin2^a)-(2y/0 -sui2y0)j (537)

4

Величина повного зусилля, яке діє на зерно

Q=Q’+Q". (5.38)

З урахуванням (5.30), (5.31), (5.33), (5.36), (5.37) формула (5.38) прийме

(5.39)

Величину кута заглиблення фа (див. рис. 5.3, а) можна знайти з виразу

Тут h — величина заглиблення зерна.

При h = г, та відповідно ра = ж/2, fit = 0,5, ф0 = я/4, формула (5.39) прийме вигляд

Q = 2km-2 —j— ■ (5.40)

4

Формулу (5.40) будемо використовувати і при розрахунку закріплення зерен із глибиною закладення h > г, тому що різальне зерно завжди заглиблено на величину менше 2г, що не дозволяє врахувати аналітично зростання зусиль закріплення, яке можна розрахувати лише при заглибленні h > 2,5г [81]. Крім того, за експериментальними даними роботи [82] збільшення заглиблення зерна на величину, яка більша радіуса, не приводить до подальшого зростання грани­чного зусилля.

Одним із вихідних даних у формулі (5.39) є пластична постійна матеріа­лу, у якому закріплене зерно. Її визначимо за формулою

2 ’

де os — межа текучості, Н/мм2.

Межу текучості матеріалу можна визначити за величиною його твердості [83]

а, = 4,2434 НВ, НУмм2.

де НВ — твердість матеріалу за Брінелем, Н/мм2.

Тоді

к = 2,1217 НВ, Н/мм2. (5.41)

Використовуючи формулу (5.39), розрахуємо граничне зусилля закріп­лення алмазних зерен зернистостей 100/80, 160/125, 315/250, 400/315 у зв’язці М2-01, а також зусилля, що виникають при втискуванні кулі діаметром 1 мм у різні матеріали (табл. 5.2), за якими виконаємо експериментальну перевірку то­чності аналітичних розрахунків. Середній еквівалентний діаметр алмазних зе­рен розраховували за формулою (2.4).

Таблиця 5.2. Механічні властивості досліджуваних матеріалів Показники Матеріали Зв’язка М2-01 Мідь Алюміній Твердість НВ 174 79 83 Пластична постійна к, Н/мм2 369,176 167,614 176,101

На рис. 5.4 наведені результати розрахунків, з аналізу яких можна зроби­ти висновок, що зі збільшенням зернистості і величини заглиблення граничні зусилля закріплення зростають. При цьому зерно може вважатися в стійкому стані при його заглибленні в зв’язку на величину h > dc/l. При заглибленні на величину dc/i зерно знаходиться в нестійкому стані, тому що сили закріплення знижуються більше, ніж у 1,33 рази.

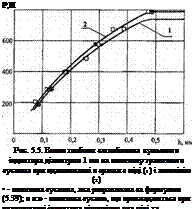
Для оцінки точності розрахунків граничних зусиль по формулі (6.39) для кульової моделі иімм були проведені експерименти по вдавлюванню кульового індентора в поліровану поверхню зразкіз із міді й алюмінію (рис. 5.5).

Експерименти проводили на приладі для виміру твердості по Роквеллу. Навантаження кульового індентора здійснювали за допомогою спеціальних ва­нтажів, які дозволяють одержати необхідні зусилля. Глибину лунки, що утво­рилася, розраховували за формулою

де <іш — діаметр кулі, що вдавлюється, мм;

dj, — діаметр лунки, мм, визначений як середнє арифметичне вимірів у двох взаємно перпендикулярних напрямках (визначався на інструментальному мік­роскопі з точністю 0,01 мм).

Дослід по вдавлюванню кульового індентора при одному і тому самому зусиллі повторювали тричі. Потім по формулі (6.39) розраховували зусилля, необхідні для одержання відбитків, ідентичних експериментальним. Розрахо­вані зусилля по розмірах трьох лунок, отриманих при одному і тому самому зу­силлі навантаження, усередювались і порівнювалися з експериментальними. Точність розрахунків оцінювали відносною похибкою

де Р3 — зусилля навантаження під час експерименту, Н;

Р — зусилля, яке розраховане за формулою (5.39), Н.

Як показали результати експериментів (див. рис. 5.5), значення є не пере­вищують 6%, що надає право використовувати запропоновану методику для розрахунку граничних зусиль закріплення алмазних зерен у металевій зв’язці.

О 0,060 0,120 0,180 0,240 h, мм

Рис. 5.4. Вплив глибини заглиблення зерна в зв’язці М2-01 на величину граничного зусилля для різних зернистостей: 1 — 100/80; 2 — 160/125; 3 — 315/250; 4 — 400/315