ІНТЕНСИВНІСТЬ ВИДАЛЕННЯ ЗВ’ЯЗКИ У ПРОЦЕСІ КЕРУЮЧИХ. ДІЙ НА РОБОЧУ ПОВЕРХНЮ КРУГА ПРИ ВІДСУТНОСТІ. ЗАСАЛЮВАННЯ МІЖЗЕРЕННОГО ПРОСТОРУ

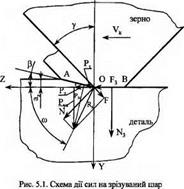
5.1 Сили різання при шліфуванні

Для розрахунку інтенсивності видалення зв’язки в процесі керуючих дій необхідно мати залежності, що описують збільшення складових сил різання в часі, обумовлене зміною параметрів РПК, та знати умови надійного закріплення алмазного зерна в зв’язці.

Сила різання на шліфувальному крузі являє собою суму сил на окремих зернах, які одночасно знаходяться в контакті з поверхнею заготовки, у зв’язку з чим спочатку визначимо силу різання на одиничному зерні.

При визначенні рівнодіючої сили різання будемо виходити з рівноваги ряду активних (зовнішніх) сил, які діють на зрізуваний шар, і реактивних (вну­трішніх) сил, які діють на алмазне зерно (рис. 5.1). До цих сил відносяться: но­рмальна сила N, із якою передня поверхня діє на зрізуваний шар, сила тертя стружки по передній поверхні F, сила нормального тиску N, задньої поверхні на поверхню різання і сила тертя F, поверхні різання об задню поверхню зерна. Складаючись, сила N і F утворюють силу стружкоутворення R„ що нахилена до поверхні різання під кутом дії и.

Розкладемо силу стружкоутворення Rs на дві: сили Рц, перпендикулярну умовній площині зсуву ОА, і силу Рп яка діє уздовж площини зсуву. Сила Рц стискує шар, що руйнується, а сила Рт зрушує його уздовж умовної площини зсуву. При цьому зсувна деформація починається в тому випадку, коли напру­ження зрушення стає рівним межі текучості оброблюваного матеріалу на зсув т„ [73].

Для визначення складової сили різання Pz і Ру сумістимо початок коорди­нат із точкою О і розкладемо силу стружкоутворення на дві складові Ра і Ру„ які діють у напрямку осей z і у.

(5.5)

Таким чином, визначення Р2 і Ру зводиться до знаходження Рп Pn, N3, F3 і кута дії ы.

Для розрахунку Р„ PN, N3 і F3 скористаємося законами розподілу норма­льних і дотичних напружень в умовній площині зсуву ОА та у зоні контакту по­верхні різання з задньою поверхнею зерна.

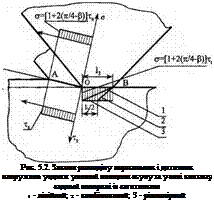
Базуючись на аналізі досліджень [46, 73, 74, 75, 76,], розподіл нормальних і дотичних напружень уздовж умовної площини зсуву приймемо рівномірним із співвідношенням а розподіл нормальних напружень уздовж площадки контакту задньої поверхні зерна будемо описувати трьома законами: лінійним, комбінованим і рівномір­ним (рис. 5.2).

Тоді середня величина нормальних напружень на площадці контакту на задній поверхні може бути розрахована за формулою

Оср = К3 а, (5.6)

де к3 — коефіцієнт, який враховує закон розподілу нормальних напружень на площадці контакту задньої поверхні зерна з поверхнею різання.

При лінійному законі розподілу к3 = 0,5; при комбінованому — 0,75 і рів­номірному — 1.

З рис. 5.1,5.2 будемо мати

де а2, Ь — товщина і ширина зрізу одиничним зерном.

Тоді, з урахуванням відношення а/т„

(5.9)

Вплив швидкості деформації і температури в умовах шліфування на ts врахуємо за допомогою модифікації К. Мак-Грегора і І. Фішера, перетворивши з

урахуванням модифікації залежність мікротвердості оброблюваного матеріалу (HV) від температури, отриману при стандартних методах іспитів, і апроксиму — вавши залежність (HV) =fiT) лінійною функцією [78]

т„ = С-аТ,

де Т- температура різання, К;

С, а — початкова ордината і кутовий коефіцієнт (табл. 5.1);

Оброблюваний матеріал	Стан	тп МПа
С	а
Швидкорізальні сталі Р18, Р14Ф4, Р12ФЗ	Загартовані	1761	0,185
Високолеговані сталі XI2Ф, Х12М, 9Х5Ф, Х6ВФ, Х6ВЗФМ	Загартовані	1697	0,148

Таблиця 5.1. Значення С і а для високолегованих і швидкорізальних

сталей

Тоді, після підстановки (5.22) у (5.20) будемо мати

+ (5.23)

Температуру різання Т знайдемо як максимальну температуру на поверх­ні заготовки під джерелом тепла [26,79]

(5.24)

nXVd

де q — щільність теплового потоку, Вт/(с-м2);

а — коефіцієнт температуропроводності оброблюваного матеріалу, м/с; X- коефіцієнт теплопровідності, Вт/(м-К);

Vd — швидкість заготовки, м/с;

Я — безрозмірна напівширина джерела.

Щільність теплового потоку

де — тангенціальна складова сили різання на шліфувальному крузі, Н;

VK — швидкість шліфувального круга, м/с;

S — площа зони контакту деталі з кругом, м2;

а* — коефіцієнт введення, що враховує частку тепла, яка надходить у загото­вку;

J — механічний еквівалент (у системі СВ J= 1).

Після підстановки (5.25) у (5.24), а потім у (5.23) і відповідних перетво­рень, отримаємо

Коректність формул (5.26), (5.27) при розрахунку складових сил різання в процесі плоского врізного алмазного шліфування сталі Р6М5ФЗ кругами з ал­мазів АС6 зернистістю 100/80, 160/125,250/200 була підтверджена експеримен­тально. При цьому розбіжність теоретично розрахованих і визначених експери­ментально величин складової сили різання знаходиться в межах 16-26%. Декі­
лька більша розбіжність спостерігається при зіставленні величин складової Ру, особливо для круга зернистістю 100/80 (до 37%). Це пояснюється впливом на Ру процесу засалювання, що у найбільшій мірі виявляється на дрібнозернистому крузі і чого не враховує розроблена методика розрахунку.

Формули (5.26), (5.27) дозволяють описати еволюцію підсистеми різання в часі. Для цього величини as zp, Ь, 13, які входять у формули, необхідно вирази­ти у функції часу шліфування, використовуючи формули розділу 2.