Математична модель робочої поверхні круга. в процесі шліфування

Виконані нами дослідження з впливу режимів шліфування на форми зрізу і відстань між контактуючими зернами дозволяють створити математичну мо­дель РПК, яка відображає реальний процес шліфування при конкретних умовах оброблення.

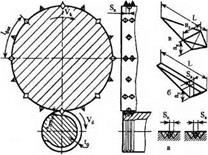
Представимо шліфувальний круг при врізному шліфуванні як сукупність статистично рівнозначних перерізів площиною, перпендикулярною осі круга (рис. 4.7).

Рис. 4.8. Модель робочої поверхні круга в процесі шліфування а — послідовність проходження зрізів; б — ідеалізована форма перекритого комоподібного зрізу; в — ідеалізована форма не перекритого комоподібного зрізу

Якщо в активній частині поверхні моделі круга в статиці зерна можуть вважатися розташованими рівномірно в напрямку вектору швидкості різання та перпендикулярно до нього, займаючи центри квадратів із розміром сторони, рі­вним ймовірному значенню кроку між активними зернами Sx, то при побудові моделі, що відображає розташування зерен на поверхні працюючого круга, та­кий підхід неприпустимий. Це пояснюється тим, що при обробці сегментоподі-

— . . . 60VK, .

сними зрізами контактуючі зерна розташовані на поверхні ^ * х 1 мм і не по­трапляють услід одне одному, а при обробці комоподібними зрізами умови ко­нтактування в напрямку вектору швидкості різання та перпендикулярно до ньо­го різні. Так, умовою контакту зерен, розташованих у площині, паралельній ве­ктору швидкості різання, буде ARUK < агтях, а в площині, перпендикулярній век­тору швидкості — ARm < іф. Відомо, що при комоподібному зрізі ґф > а7тт.

Фактична окружна відстань між зернами, що контактують, у статистично рівнозначних перерізах не виключає появи комоподібної форми, тобто подовж­нього перекриття зрізів. У зв’язку з тим, що на поверхні математичної моделі
розміром Іфок хі мм у перерізі, паралельному вектору швидкості контактує ли­ше одне зерно, інші контактуючі зерна, які розташовані на цій поверхні, не по­трапляють услід одне одному та утворюють умовний поперечний різальний профіль. Зміщення зерен умовного різального профілю визначає поперечне зміщення Sx статистично рівнозначних перерізів. Зерна одного перерізу орієн­товані щодо зерен іншого перерізу довільно, у силу чого послідовність прохо­дження зрізів може порушуватися (див. рис. 4.7, в).

У випадку поперечного перекриття зрізів об’єм одиничного зрізу спроще­но можна представити у вигляді двох напівпризм (див. рис. 4.7, б), а у випадку відсутності перекриття — у вигляді двох пірамід (див. рис. 4.7, а).

Запропонована математична модель робочої поверхні не є незмінною для усіх випадків шліфування, а в залежності від конкретних умов може змінюва­тися. Наприклад, якщо ІфЖ забезпечує сегментоподібний зріз, a Sx таке, що зер­на перекриваються, маємо модель О. В. Нікольского, а якщо Іфок забезпечує сег­ментоподібний зріз, a Sx не забезпечує перекриття — маємо модель І. М. Брозголя [68].

Фактична окружна відстань між зернами Іфок у залежності від характерис­тик алмазовмісного шару і режимів шліфування визначається за формулою (4.3), яка з урахуванням її складових (2.28) і (4.2) прийме вигляд:

(4.20)

Відстань між перерізами Sx знайдемо, використовуючи поняття ефектив­ного різального профілю [69].

Цей умовний профіль на поверхні різання формується контактуючими зе­рнами, розташованими на поверхні Іфт х 1 мм, які рівномірно зміщені в попе­речному напрямку. У цьому випадку відстань між перерізами

(4.21)

З урахуванням (4.19) ймовірна кількість зерен, що контактують, на пове­рхні ІфаК хі мм, буде дорівнювати

(4.22)

Тоді, після підстановки (4.22) у (4.21), будемо мати

(4.23)

Геометричні параметри алмазних зерен визначаються за формулами (2.3), (2.18), (2.21), (2.23).

4.3 Розрахунок розмірів одиничних зрізів на базі математичної
моделі робочої поверхні круга

Розміри одиничного зрізу описуються довжиною, фактичною товщиною і шириною зрізу.

Довжина сегментоподібного зрізу розраховується за формулою (3.12), комоподібного — за формулою

(4.24)

Максимальна товщина сешентоподібних зрізів дорівнює фактичній гли­бині різання. Вперше термін «фактична глибина різання» був введений Е. М. Масловим, щоб підкреслити істотне розходження між глибиною різання при обробленні лезовим інструментом та при шліфуванні.

Як установлено нами [70], у результаті відсутності суцільної різальної кромки на РПК вплив подачі на врізання t на фактичну глибину різання зале­жить від співвідношення величини подачі і максимальної висоти нерівностей шліфованої поверхні Rmax.

Оскільки видалення матеріалу комоподібними зрізами здійснюється з по­верхні різання також в умовах відсутності суцільної різальної кромки, то, за аналогією з глибиною різання, максимальну товщину зрізу необхідно оцінюва­ти максимальною фактичною його товщиною, з огляду на співвідношення ве­личини az гоах та максимальної висоти нерівностей профілю поверхні різання

Для розрахунку висоти нерівностей поверхні різання була розроблена ме­тодика [71], яка дозволяє установити, шо Кпжпр перевищує агпах. Тоді максима­льна фактична товщина зрізу

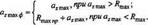(4.26)

Максимальна товщина комоподібного зрізу а2 розраховується за фор­мулами (3.31), (3.32), (3.33).

Ширина зрізів при відсутності їх перекриття в поперечному напрямку функціонально залежить від товщини зрізу і визначається формою різального виступу. Якщо виступ має форму конуса з округленою вершиною, то поперечна форма зрізу буде складатися із сегментоподібної і трапецеїдальної ділянок, а ширина зрізу може бути розрахована за формулою Е. М.Маслова [32, 72]:

Ъ’г = 2^2раг-а + (а’2 — az)tg£n (4.27)

де Ьг — ширина профілю для довільної точки т поперечного перерізу, мкм; р — радіус округлення вершини, мкм; єп — кут профілю зерна, град;

а„ а- глибини перерізу, які відповідають сегментопсдібній ділянці профі­лю і розглянутій точці, мкм.

При наявності поперечного перекриття форма поперечного перерізу може розглядатися у вигляді прямокутника розмірами Sx*a2 твх ф. У цьому випадку ширина зрізу Sx розраховується за формулою (4.23).