КІНЕМАТИКА ШЛІФУВАННЯ ПЕРИФЕРІЄЮ КРУГА. Траєкторія абразивного зерна відносно деталі

У процесі шліфування алмазні зерна, які розташовані на робочій поверхні круга, здійснюють відносно деталі переміщення по траєкторіях, обумовлених заданими робочими рухами. Траєкторії зерен визначають форму обробленої по­верхні, а також форми й розміри частинок металу, які видаляються, тобто зрізів, що впливає на умови роботи круга та вихідні параметри шліфування.

Розглянемо траєкторію зерна на прикладі найбільш складного з погляду кінематики внутрішнього шліфування з безперервними подовжньою і попере­чною подачами, яке охоплює усі різновиди внутрішнього шліфування перифе­рією круга.

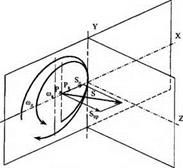
Принципова кінематична схема різання при внутрішньому шліфуванні з безперервними подовжньою і поперечною подачами (рис. 3.1) включає два рів­номірні обертальних рухи деталі озд і круга та один прямолінійний S, що спрямований під кутом до осі деталі. Прямолінійний рух S є результуючим двох рівномірних безперервних подач — поперечної S„ і подовжньої S„p.

Описана кінематична схема охоплює усі види внутрішнього шліфування: при iS„ = 0 маємо внутрішнє шліфування з безперервною подовжньою подачею і дискретною поперечною; якщо 5^ = 0 — внутрішнє врізне шліфування.

При виводі рівняння траєкторії абразивного зерна відносно деталі для зу­стрічного внутрішнього шліфування скористуємося наступною методикою.

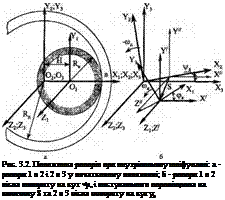
Нехай репер 1, жорстко зв’язаний із шліфувальним кругом, обертається навколо осі Z (рис. 3.2) і поступально переміщується в площині X202Z2 віднос­но репера 2. Останній обертається навколо осі Z^, і його початок збігається з репером 3, який жорстко зв’язаний із деталлю. Репер 2 обертається відносно ре­пера 3 із кутовою швидкістю ид.

Число пар рухів к у розглянутому випадку дорівнює двом, причому в другій парі поступальне переміщення відсутнє. Підставляючи в загальне рів­няння [64]

Рис. 3.1. Кінематична схема внутрішнього шліфування

1 0 0

те2 = 0 1 0 — матриця кутового положення реперів; 0 0 1

матриця поступального переміщення.

Для того щоб зберегти загальноприйнятий порядок обчислення матриць, перепишемо рівняння (3.1)

т-і = тлт^2тл т¥хт = т^2{Щ + тс]), (3.2)

Підставивши значення матриць у рівняння (3.2), після перетворень і спрощень одержимо:

Таким чином, траєкторія абразивного зерна відносно деталі для внутріш­нього зустрічного шліфування з безперервними поперечною і подовжньою по­дачами з урахуванням того, що = іфк, у координатному записі визначиться системою параметричних рівнянь:

(3.3)

де фк — параметр.

Аналогічно були отримані рівняння траєкторії абразивних зерен відносно деталі при попутному шліфуванні, спільний запис яких із рівняннями для зу­стрічного шліфування має вигляд

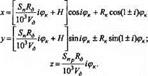(3.4)

де Н = Rj> — RK — ексцентриситет між осями обертання деталі і круга, мм;

Rd, RK — радіуси деталі, що шліфується, і круга відповідно, мм;

. в>л VdRK. .

і = —— = ——— співвідношення між кутовими швидкостями деталі і кру-

а>к 60 VKRd

га;

фк~ кут повороту круга, рад;

S„, S^p-поперечна і подовжня подача, мм/хв;

ий, ик — кутові швидкості деталі і круга відносно центрів обертання, 1/с;

Vs, VK — окружні швидкості деталі, м/хв, і круга, м/с, відповідно.

Тут і далі верхні знаки відносяться до випадку обертання деталі і круга в протилежних напрямках, нижні — в одному напрямку.

Якщо внутрішнє шліфування здійснюється з безперервною подовжньою і дискретною поперечною подачами (S„ = 0), рівняння траєкторії абразивних зе­рен відносно деталі буде мати вигляд

де — подовжня подача, віднесена до одного оберту деталі.

При внутрішньому врізному шліфуванні (5^ = 0) із безперевною попере­чною подачею траєкторія абразивних зерен описується системою рівнянь

При круглому зовнішньому шліфуванні з дискретною поперечною пода­чею траєкторія руху абразивного зерна описується системою

(3.7)

neH=RK + R&

3.2 Вплив напрямку обертання круга і деталі на траєкторію
руху абразивного зерна

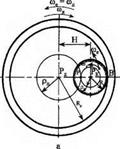
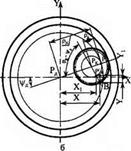
Для вивчення впливу напрямку обертання круга і деталі на вид траєкторії скористаємося методом обертання руху [60]. Відомо [65], що будь-який плос­кий рух може бути поданий як кочення без ковзання деякої рухомої кривої, зв’язаної з плоскою фігурою по деякій нерухомій кривій. Виходячи з цього, знайдемо траєкторію руху абразивних зерен для випадків зустрічного і попут­ного внутрішнього шліфування (рис. 3.3, а; 3.4, а).

Приймемо плоску кінематичну схему різання та припустимо, що попере­чна подача здійснюється дискретно на кожний оберт деталі. Така схема буде відповідати внутрішньому шліфуванню методом врізання з дискретною пода­чею. Співвідношення між кутовими швидкостями, числами обертів, окружними швидкостями круга і деталі виражається залежностями

і = ^д_=Щ= У_дК__ (3.8)

«V и« 60 VKRd

Припустимо, що рух вершини абразивного зерна відбувається відносно нерухомої деталі.

Рис. 3.3. Схема для визначення траєкторії руху абразивних зерен відносно деталі при внутрішньому шліфуванні для випадку обертання деталі і круга в протилежних напрямках

Рис. 3.4. Схема для визначення траєкторії руху абразивних зерен відносно деталі при внутрішньому шліфуванні для випадку обертання деталі і круга в одному напрямку

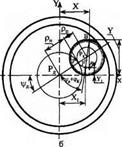
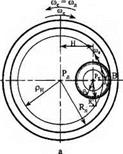
Для цього системі деталь-круг умовно надамо додаткове обертання на­вколо осі деталі з кутовою швидкістю яка дорівнює за абсолютним значен­ням кутовій швидкості деталі, але протилежна за напрямком. При цьому швид­кість деталі стане рівною нулю, а круг одержить, крім відносного руху з куто­вою швидкістю проти годинникової стрілки навколо власної осі Рк, ще і до­датковий рух навколо осі деталі Р* спрямований також проти годинникової стрілки з кутовою швидкістю ше. Схема описаного руху приведена на рис. 3.3, б; 3.4, б.

При додаванні швидкостей переносного оіе і відносного озк рухів миттє­вий центр швидкостей лежить на відрізку, який з’єднує переносний і відносний миттєві центри Рк і Рд і поділяє цей відрізок на частини, зворотно пропорційні СОй і [60], тобто

(3.9)

Абсолютний рух вершини абразивного зерна В відносно нерухомої деталі можна розглядати як кочення без ковзання рухомої центроїди, зв’язаної зі шлі­фувальним кругом, по нерухомій. Оскільки обидві центроїди є колами і рухома котиться по нерухомій без ковзання, то точка, яка належить рухомій центроїді, буде описувати епіциклоїду при зустрічному і гіпоциклоїду — при попутному шліфуванні. Рівняння руху точки Р у прямокутній системі координат із почат­ком у центрі нерухомої центроїди буде мати вигляд (див. рис. 3.3, б; 3.4, б)

Підставивши значення ірд у рівняння (3.17) і перетворивши його, одержи­мо:

x = Hcosi<pK + RK cos(<pK ± ^6);] у = Hsmi<pK ± RK sin(^ ± Wd)

Якщо до рівняння (3.19) траєкторії руху точки В вершини абразивного зерна в обертальному русі приєднати рівняння відносного переміщення її уз­довж осі Z деталі, то одержимо траєкторію руху вершини абразивного зерна при внутрішньому шліфуванні з подовжньою подачею, яка описується систе­мою рівнянь, аналогічною (3.5).

За допомогою даної методики була отримана система рівнянь, яка визна­чає траєкторію руху абразивного зерна при круглому зовнішньому шліфуванні з безперервною подовжньою і дискретною поперечною подачами, що ідентична

У випадку, коли = 0, траєкторіями вершини абразивного зерна віднос­но деталі при круглому зовнішньому шліфуванні з дискретною поперечною по­дачею буде подовжена епіциклоїда (епітрохоїда) при різних напрямках обер­тання круга і деталі та подовжена гіпоциклоїда (гіпотрохоїда) — при однакових.

Таким чином, траєкторія руху абразивного зерна як при внутрішньому, так і при круглому зовнішньому шліфуванні з безперервною подовжньою пода­чею є подовжена епіциклічна гвинтова крива (гвинтова епітрохоїда) при обер­танні деталі і круга в протилежних напрямках і подовжена гіпоциклічна гвин­това крива (гвинтова гіпотрохоїда) при обертанні в одному напрямку.

Траєкторією руху вершини абразивного зерна відносно деталі при плос­кому шліфуванні є трохоїда як при однакових напрямках векторів швидкості деталі і круга, так і при різних, яка описується системою рівнянь

(3.20)