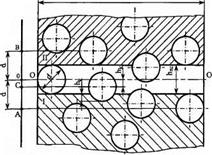
Робоча поверхня нерухомого круга утворюється алмазовмісним шаром, який представляє собою абразивний простір, що складається із зв’язки, в об’ємі якої рівномірно розподілені різноманітно орієнтовані алмазні зерна довільної геометричної форми.
У зв’язку з цим при аналітичному описі робочої поверхні скористаємося методами математичної статистики, а реальну форму алмазних зерен замінимо еквівалентною моделлю простої геометричної форми. У якості моделі алмазного зерна будемо використовувати суцільну кулю певного радіуса, маса якої дорівнює математичному очікуванню маси абразивного матеріалу, що припадає на одне зерно [43]. „ .
Середній розмір еквівалентної кулі знайдемо, скориставшись рекомендаціями [43,49]. Кількість зерен Nz у навісці
Nz =—, (2.2)
Р
де q _ навіска абразивного порошку, г;
р _ середня маса одного зерна, г.
Виразимо масу одного зерна через об’єм і густину речовини [49, 50]
з Р = уК0<?. (2.3)
Тут у — густина алмаза, г/см ;
d-еквівалентний усереднений діаметр алмазного зерна, мкм;
К0 — коефіцієнт заповнення об’єму частками неправильної форми.
°Після підстановки (2.3) у (2.1) і з урахуванням того, що для алмазного порошку 7= 3,53 г/см3; Q ~ 0,2 г; К0 = 0,25 [49]; діаметр моделі зерна буде дорівнювати
Відстань між алмазними зернами в перерізі алмазовмїсного шару площиною знайдемо у припущенні, що алмазовмісний шар являє собою абразивний простір із наступними властивостями [43]: число часток прагне до нескінченності; густина часток у будь-якій частині простору постійна; об’єм простору, що припадає на одну частку, постійний; частки в просторі нерухомі і зафіксовані середовищем, яке ототожнюється із самим простором; властивості простору ізотропні; всі алмазні зерна приведені до форми пулі з середнім розміром d.
У такому абразивному просторі кожній характеристиці алмазного круга відповідає певна кількість зерен, яка у каратах складе
|
|
де К — відносна концентрація алмазовмісного шару.
Кількість зерен у 1 см3 абразивного простору
Пу — iNz, шт/см3, (2.6)
де Nz — середня кількість зерен в одному караті.
Середня кількість алмазних зерен в одному караті може бути визначена за даними роботи [50], або розрахована з використанням середнього зваженого кубічного розміру частки [49]
Nz =-^хЮ9, шт/карат. dсп
Тоді відстань між зернами в перерізі алмазовмісного шару площиною буде дорівнювати
•*-$? <27)
2.2 Кількість алмазних зерен і відстань між ними на робочій поверхні нерухомого шліфувального круга
Утворення робочої поверхні шліфувального круга представимо як формування поверхні розділу абразивного простору необмежених розмірів, у якому статистично рівномірно із заданою щільністю розподілені алмазні зерна з розмірами d.
Виділимо з абразивного простору об’єм W (рис. 2.3).
ЇТ = 1хЯхоо,
де 1 — одинична товщина об’єму, яка дорівнює розміру простору, що доводиться
на одне алмазне зерно в напрямку, перпендикулярному площині креслення;
в _ ширина абразивного простору;
оо_ розмір абразивного простору в напрямку, перпендикулярному ширині.
|
В
|
рис. 2.3. Схема поділу частини абразивного простору шириною В
площиною 0-0
Розглянемо розчленовування виділеного об’єму на частини І і II площиною 0-0-
Спроектуємо центри зерен, що знаходяться в об’ємі 2dxBxl на площину АВ розмірами 2d у І, розташовану перпендикулярно площині рознімання. Тоді зерна, проекції центрів яких потрапили на площину ОА у 1, будуть належати частині абразивного простору І, а на площину ОВ у 1 — частині простору
З урахуванням сказаного, кількість зерен на поверхні об’єму І визначиться формул010
Zi = Z„Pu (2.8)
де z — кількість зерен, які знаходяться в об’ємі абразивного простору розміром 2dxB*l>
р{ _ ймовірність того, що проекції центрів зерен потрапили на площину 04×1-
Вказана ймовірність дорівнює
Таким чином, кількість зерен, які потрапили на поверхню рознімання і належать частині І, у 1/2 разу менше кількості зерен у матриці, які перетинаються площиною, еквідистантною площині рознімання. Сказане однаковою мірою відноситься і до частини II.
У дійсності робоча поверхня алмазного круга формується трохи по — іншому, ніж описано вище. Для розміщення стружки, що зрізається, шляхом видалення зв’язки утворюється міжзеренний простір. У результаті видалення зв’язки може бути сформована робоча поверхня глибиною h„c, y яку утворять зерна, розташовані в об’ємі d х В х 1, що прилягає до площини рознімання О — О.
У силу того, що при правці, а потім при шліфуванні, на алмазні зерна діє сила різання, не всі зерна, кількість яких визначена за рівнянням (2.8), утримуються зв’язкою. На робочій поверхні утримуються лише ті зерна, глибина розташування яких у зв’язці більше критичної глибини закладення hy.
Тоді (див. рис. 2.3), ймовірність того, що проекції центрів зерен потраплять на поверхню площини АВ розміром {d — hK ) х 1 буде дорівнювати
![]() (2.10)
(2.10)
Для того щоб ці зерна належали частині І абразивного простору, необхідно, щоб одночасно з виконанням умови (2.10) була виконана умова (2.9), тобто загальна ймовірність складала
Р = Р1хР2.
або, з урахуванням (2.9) і (2.10)
![]() (2.11)
(2.11)
З огляду на те, що розглянутий абразивний простір має властивість сталості щільності часток у будь-якій його частині і у будь-якому напрямку, формула (2.11) може бути застосована не тільки до виділеного об’єму одиничної товщини, але й до їх сукупності в напрямку, перпендикулярному площині креслення (див. рис. 2.3).
Тоді, кількість зерен на одиниці робочої поверхні круга, виражена через кількість зерен на 1 мм5 перерізу абразивного простору площиною, буде
риментально, як вибіркову середню, визначену за результатами обробки профі — лограми, яка включає 200 алмазних зерен, записаної на спеціальній установці [51], яка забезпечує автоматичне виділення рельєфу зерен із сумарного рельєфу зерен і зв’язки. Як видно з приведених даних (табл. 2.1), відстані між зернами, розраховані за формулою (2.16) для різних станів РПК, що характеризуються критичним розміром закладення зерен у зв’язці К, добре співпадають з даними експерименту.
|
Таблиця 2.1. Відстані між алмазними зернами на робочій поверхні ___________ шліфувальних кругів____________________________
|
Проаналізуємо вплив критичної глибини закладення зерна, яка залежить від здатності зв’язки утримувати зерно від випадання, на величину коефіцієнта Ки який показує, в скільки разів середня відстань між зернами на РПК перевищує відстань між зернами в перерізі матриці алмазовмісного шару площиною.
Аналітично коефіцієнт К знаходимо за формулою (2.15), а експериментально — за наступною залежністю
де S, — середня відстань між зернами на поверхні РПК, яка визначена в результаті обробки профілограми робочої поверхні круга;
8зр — відстань між зернами в перерізі матриці алмазовмісного шару площиною, яка розрахована за формулою (2.7).
Результати досліджень подані в табл. 2.2.
|
Шліфувальний круг |
мм |
Розрахунок за формулою (3.15) |
Заданими експериме нту |
|
|
h=-d к 2 |
||||
|
АС6 100/80-4-М2-01 |
0,13 |
2,82 |
2,45 |
2,59 |
|
АС6 160/125-4-М2-01 |
0,21 |
2,45 |
||
|
АС6 250/200-4-М2-01 |
0,30 |
2,36 |
|
Таблиця 2.2. Вплив міцності закріплення зерна в зв’язці на значення |
|
коефіцієнта Кх |
Таким чином, середня відстань між зернами на РПК залежить не тільки від зернистості і відносної концентрації алмазів, але й від міцності утримання зерен зв’язкою. За рівних інших умов, збільшення міцності утримання зерен зв’язкою сприяє зменшенню відстані між зернами на РПК.