ПАРАМЕТРИ РОБОЧОЇ ПОВЕРХНІ АЛМАЗНОГО ШЛІФУВАЛЬНОГО. КРУГА В СТАТИЦІ

2.1 Існуючі моделі алмазних зерен та області їх застосування

Видалення матеріалу з поверхні оброблюваної заготовки при шліфуванні виконується зернами абразивного матеріалу, які є різальними елементами ро­бочої поверхні абразивного інструменту. Геометрична форма абразивного зерна в цілому та тієї його частини, яка безпосередньо приймає участь у процесі рі­зання, є одними з найбільш істотних факторів, що визначають процес різання при шліфуванні.

Питанням визначення геометричної форми і її параметрів для абразивних і алмазних зерен присвячена велика кількість досліджень, що розрізняються, по-перше, підходом до опису робочої поверхні круга, по-друге, застосовувани­ми методами вимірів, і, по-третє, видами моделей, які описують складну форму реального зерна.

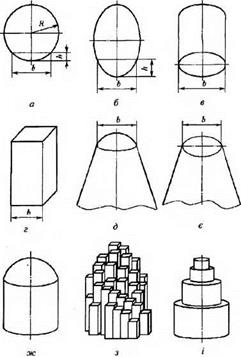
При аналітичних розрахунках сил різання, параметрів шорсткості шліфо­ваної поверхні, локальних температур і інших показників процесу шліфування реальна форма зерна заміняється дослідниками спрощеним геометричним ті­лом: кулею (рис. 2.1, а) [31,32,33], еліпсоїдом обертання (рис. 2.1, б) [2, 31,34], циліндром (рис. 2.1, в) [35], прямокутним паралелепіпедом (рис. 2.1, г) [36], а форма різальної частини — конусом з округленою або загостреною вершиною (рис. 2.1, д), усіченим конусом (рис. 2.1, е) [32, 37, 38], кульовим сегментом (рис. 2.1, ж) [39, 40], набором призм (рис. 2.1, з) або циліндрів (рис. 2.1, і) [41], мікровиступами на поверхні еліпсоїда обертання зі середньоймовірним кутом розходження 2<р [42], різальною кулею, що має суцільну серцевину і кульовий пояс, який складається з різальних точок із нерівномірною щільністю по глиби­ні останнього [43].

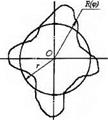
Відповідно до останніх досліджень [44], геометричну форму профілю зе­рна в деякій фіксованій площині (рис. 2.2) у загальному вигляді описують ана­літично стаціонарною випадковою функцією виду

р

R(q>) = r+ ■ sin(^ + <рк), (2.1)

к=г

де R((p) — значення полярного радіуса точок профілю зерна при фіксованому значенні полярного кута щ г — радіус середньої окружності профілю зерна; к — номер гармоніки;

Ак, <рк — випадкова амплітуда і фаза, що відповідає к-й гармоніці; р — порядковий номер кінцевої гармоніки, яка складає нерівності абразив­ного зерна.

Рис. 2.1. Моделі абразивних зерен та їх різальних частин

Рис. 2.2. Контур проекції абразивного зерна на площину [44]

Різноманітність запропонованих моделей зерен обумовлена не стільки рі­зницею використовуваних підходів і методик, скільки характером розв’язуваної за допомогою даної моделі задачі.

Так, у роботі [44] відзначається, що, незважаючи на наявність практично у всіх абразивних зерен гармонік із дуже великим порядковим номером, вибір розміру р у рівнянні (2.1) залежить від кінцевої мети досліджень геометричної форми зерен. Наприклад, якщо кінцева мета — визначення числа зерен в одини­ці об’єму або площі канавок від зерен при великих глибинах їх занурення в по­верхню, то геометричну форму профілю зерна можна представити окружністю радіуса г. Якщо необхідно розрахувати розташування зерен, орієнтованих на робочій поверхні інструменту великою діагоналлю, у рівнянні (2.1) виділяється друга гармоніка і т. д.

Таким чином, вибір моделі абразивного й алмазного зерна при розв’язанні конкретної задачі в кінцевому рахунку визначається функцією, яку виконує зе­рно в даній задачі. Зазначимо функції, які може виконувати зерно в абразивно­му інструменті:

1) складова частина рецептури інструменту або його алмазовмісного ша­

ру;

2) елемент робочої поверхні інструменту, який формує її макропрофіль;

3) елемент робочої поверхні інструменту, який визначає мікропрофіль її різальних частин;

4) різальний елемент робочої поверхні, який повинен відповідати вимо­гам технічних умов.

Відповідно до виконуваної функції при визначенні об’єму міжзеренного простору використовується модель зерна у формі кулі [43], при аналізі просто — пової орієнтації зерен — у формі конуса [37], при визначенні розмірів одиничних зрізів — У формі конуса з усіченою вершиною [38].

V Моделі зерна у формі абсолютно гладкого тіла або індентора з гладкою поверхнею показали свою придатність при здійсненні зерном 1-ї і 2-ї функцій [45]’ кульова модель — при визначенні числа зерен на поверхні абразивного ін­струменту [34, 43], модель у вигляді конуса з округленою вершиною — при ви­значенні параметрів шорсткості обробленої поверхні [37], модель у вигляді ко­нуса або призми з контактною площадкою в напрямку, перпендикулярному ве­кторові швидкості круга — при розгляді механізму руйнації оброблюваного ма­теріалу та визначенні сил тертя в зоні контакту інструмент-заготовка [46, 47, 48].