НАЛАДКА И АВТОМАТИЗАЦИЯ. БЕСЦЕНТРОВЫХ СУПЕРФИНИШНЫХ СТАНКОВ

7.1. Теоретические основы наладки бесцентровых суперфинишных станков

При бесцентровом суперфинишировании точность формооб­разующей траектории непосредственно определяет профиль про­дольного сечения заготовок. Так, для формообразования цилинд­рической поверхности необходима прямолинейная траектория, па­раллельная направлению осцилляции шлифовальных брусков, а для бомбинированной поверхности — дуговая траектория с ра­диусом, согласованным по величине с радиусом профиля детали.

Валковое устройство суперфинишного станка предназначе­но для одновременного базирования и создания движения пода­чи, что достигается пространственным перекрещиванием осей двух валков. Формообразующая траектория зависит от геомет­рии валков и параметров наладки — угла перекрещивания 2Х и межосевого расстояния 2v.

Расчет наладочных параметров проводят:

• при проектировании валкового устройства для опреде­ления оптимальных геометрических, а затем кинематических и силовых параметров процесса;

• при подналадке станка при использовании одного и того же валкового устройства для обработки цилиндрических загото­вок различных размеров;

• при эксплуатации валков с геометрией, не соответст­вующей теоретической, вследствие технологических трудностей их изготовления (например, при обработке бомбинированных поверхностей).

Для наладки бесцентрового суперфинишного станка необ­ходимо рассчитать формообразующую траекторию в зависи­мости от профиля валков и параметров валкового устройства.

Математическая модель для анализа формообразующей траек­тории была впервые создана авторами, а затем развита для случая пространственной траектории заготовок [70].

Геометрическая модель для анализа формообразующей траектории при бесцентровом суперфинишировании

Рассмотрим математическую модель для анализа формообра­зующей траектории, в которой заготовка представлена с учетом ее длины и положения в системе суперфинишного станка, в об­щем случае заданного шестью координатами (тремя координата­ми центра и тремя поворотами вокруг осей декартовой системы координат). В условно неподвижной системе координат Sz станка вводят совокупность плоских сечений Zz = Zi, в которых валки и заготовка находятся в дискретном контакте. Определение фор­мообразующей траектории без нарушения общности сводится к установлению положений оси заготовки в сечениях при ее од­новременном контакте с правым и левым валками.

Для решения контактной задачи используем основную тео­рему пространственных зацеплений. Для взаимно огибаемых поверхностей должно выполняться равенство радиус-векторов r и касательных т в контактных точках поверхностей в единой условно неподвижной системе координат. Аналитическим экви­валентом одновременного контакта заготовки с правым и левым валками является система векторных уравнений:

где гЗЛ, гЗП — радиус-векторы точек контакта на поверхности за­готовки с левым и правым валком; гВ, гВ — радиус-векторы точек контакта на поверхности левого и правого валка; тЛ, тП,

Тв, тП — нормированные касательные к точкам контакта на по­верхности заготовки левого и правого валка соответственно.

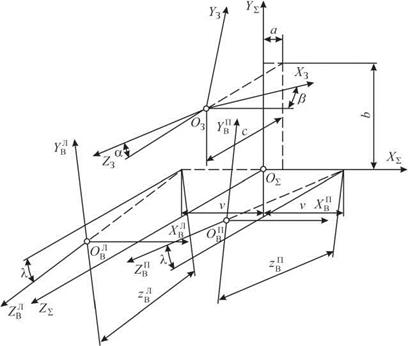
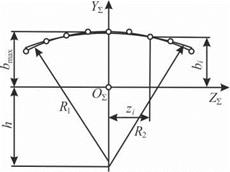
Формообразующую систему представим в виде совокупности следующих координатных систем (рис. 7.1): Sz(X-z О^ Y^ Z3) — ус­ловно неподвижная система, связанная со станиной станка; S3(X3 ОЗ

Y3 Z3) — система заготовки; SB? (XВ? ОВВ Y^1 ZВ?) — система левого валка; SBB (XП ОВВ Y^1 ZВВ) — система правого валка. Система ко­ординат S3 относительно системы S^: повернута вокруг оси X% на угол а и смещена на величину а, повернута вокруг оси Y^ на угол в

Рис. 7.1. Координатная схема бесцентрового суперфинишного станка

и смещена на величину b, смещена по оси Z^ на величину с. Пово­рот системы S3 относительно системы S’z вокруг оси Z’z не введен, поскольку он определяет лишь начало отсчета криволинейной уг­
ловой координаты поверхности заготовки. Системы координат SB и SB относительно системы Sx смещены по осям zB и ZB на ве­личины ^Л и zB, повернуты вокруг оси Хх на угол X против и по часовой стрелке и смещены на величины —v и v соответственно.

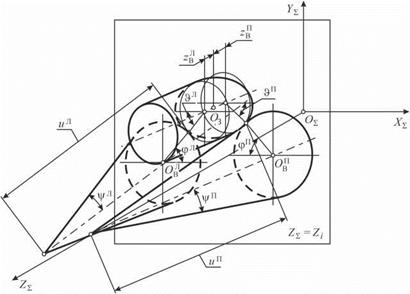
Валки представляют собой тела вращения, как правило, со сложным профилем осевого сечения, который рассчитывается для конкретных размеров заготовки и параметров наладки стан­ка. Поэтому опишем валки как совокупность усеченных кону­сов, каждый из которых задан радиусом R основания, углом у образующей и координатой zB, отсчитываемой вдоль оси конуса. Радиус R основания конуса равен радиусу профиля валка, а угол у образующей — углу касательной к осевому профилю валка в сечении zB. Заготовка в большинстве случаев имеет исходно ци­линдрическую поверхность.

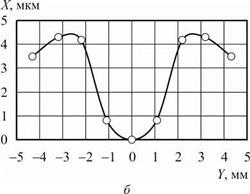
Поверхность цилиндрической заготовки в векторно­параметрической форме в системе S3 опишем следующими уравнениями (рис. 7.2):

— левая сторона:

г3л = — r cosФЛ — i — r sinЬл ■ j + z^ — к, (7.2)

— правая сторона:

гЗП = r cosФП ■ i — r sin дП ■ j + zn ■ к, (7.3)

где r — радиус заготовки; ФЛ, ФП, Z31, zn — угловая и линейная координаты цилиндрической поверхности заготовки.

Поверхность валка, как поверхность конуса, в параметриче­ском виде опишем следующими уравнениями в системах SB и SB соответственно:

— левый валок:

XB = и Л sin уЛ cos фЛ;

YB = и Л sin уЛ sin фЛ;

ZB = R ЛctgyЛ — и Л cos уЛ,

XВ1 = — ип sin уп cos фп;

УВП = ип sin уп sin фп;

ZB = Rпctgyп — ип cos уп,

где Rn, Rп — радиусы оснований конусов; фЛ, фп, иЛ ип — угловая и линейная координаты конической поверхности; уЛ, уп — углы образующих конусов левого и правого валка соответственно.

Рис. 7.2. Схема для определения углов контакта при анализе формооб­разующей траектории при бесцентровом суперфинишировании

 

Уравнения (7.2) и (7.3) заготовки при переходе в систему координат Sz преобразуют на основе формул:

ХХЗ = XЗ cosp + ZЗ sin р + а;

У^З = УЗcosa — (X^inp — ZЗ cos в) sin a + b; > Zzз = — УЗ sina — (ХЗ sinp — Zз cos p) cos a + c.

В выражении (7.6) индексы, характеризующие правую или левую контактную сторону заготовки, для упрощения записи не указаны, так как преобразования идентичны.

Уравнения (7.4) и (7.5) валков при переходе в систему коор­динат Sz преобразуют следующим образом:

— левый валок:

XЛ = XВ — v;

Yb = Y-в cosX — (ZB + zB) sin X; > ZВв = Ybb sinX + (ZB + zB) cos X;

— правый валок:

= XB + v;

YB = YBB cosX + (ZB + zB) sin X; > Z^Bb = — YBnsinX + (ZB + zB) cos X;

где 2X — угол перекрещивания осей валков; 2v — межосевое рас­стояние валков; zB, zB — координата, задающая осевое поло­жение текущего конуса относительно точки 0z перекрещивания осей валков.

Выражения для нормированных касательных к поверхно­стям в системе координат Sz имеют вид:

— левая сторона заготовки:

ТХ = — sindBcospB;

= cos^B cos аЛ + sin дЛ sin aЛ sin рЛ; (7.9)

xBZ = — cosdB sin aЛ + sin cos aЛ sin рЛ;

— правая сторона заготовки:

= sindB cosPn;

x|Y = cosdn cos aB — sin dn sin aB sin pB; (7.10)

t^Z = — cosdB sin aB — sin dB cos aB sin pB;

ТВЛ =-cosy ^тфЛ;

= cos^Л cos фЛ cos X — sin уЛ sin X; т|Л = cosyЛ cos фЛ sin X + sin уЛ cos X;

— правый валок:

= cosy ^тфП;

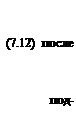= cosyП cos фП cos X + sin уП sin X; т^Л = — cosyП cos фП sin X + sin уП cos X.

В окончательном виде система уравнений (7.1) становки в нее выражений (7.2)-(7.12) примет вид

f1 = и Л sin уЛ cos фЛ + r cos ФЛ cos Р-

— zЛ sin Р — v — a = 0;

f2 = и Л sin уЛ sin фЛ cos X + A sin X + r sin дЛ cos a + + B sin a — b = 0;

f = и Л sin уЛ sin фЛ sin X + A cos X — r sin ФЛ sin a­- B cos a — c = 0;

f4 = иП sin уП cos фП + r cos ФП cos P + z^1 sin P­- v + a = 0;

f5 = и П sin уП sin фП cos X — C sin X + r sin дП cos a + + D sin a — b = 0;

f6 = иП sin уП sin фП sin X — C cos X + r sin дП sin a + + D cos a + c = 0;

f7 = sin дЛ cos P — cos уЛ sin фЛ = 0; f8 = cos ФЛ cos a + sin уЛ sin a sin p —

— cos уЛ cos фЛ cos X + sin уЛ sin X = 0;

f9 = cos ФЛ sin a-sin уЛ cos a sin в +

+ cos уЛ cos фЛ sin X + sin уЛ cos X = 0; f10 = sin ФП cos в — cos уП sin фП = 0; f11 = cos ФП cos a-sin уП sin a sin в- )

— cos уП cos фП cos X — sin уП sin X = 0; f12 = cos ФП sin a + sin уП cos a sin в —

— cos уП cos фП sin X + sin уП cos X = 0;

где A = R Л^уЛ — u Л cos уЛ + z^;

В = r cos ФЛ sin в + cos в ;

C = RП^уП — uП cos уП + z^ ;

D = — rcos ФП sin в + z^ cos в.

Для решения системы трансцендентных уравнений (7.13) используем метод параметрической оптимизации, при котором минимизируется целевая функция Ф:

Ф(^Л, ^П, z^-, z^1, фЛ, фП, иЛ, иП, a, в, a, b, c) =

=Zf? ^ min.

i=1

При решении системы (7.13) необходимо учитывать сле­дующие особенности. Задав плоское сечение (положив = Z,),

уравнения f = 0 и f6 = 0 превращают в тождества (рассматри­ваемые отдельно для каждого из валков и заготовки), из кото­рых выражают неизвестные параметры z^ , z^, иЛ, иП и под­ставляют их в уравнения f1 = f2 = f3 = f4 = 0, что позволяет сокра­тить систему (7.13) до 10 трансцендентных уравнений. Коорди­наты a, b, c определяют положение точки на оси заготовки, от­носительно которой она поворачивается на углы a и в. Чтобы

координаты а и b определялись именно в сечении Zz = Z, следу­ет положить параметр с = Zi. В результате число неизвестных параметров, подлежащих определению на основе оптимизации целевой функции Ф, сокращается с 13 до 8.

Целевая функция Ф, представляющая собой сумму квадра­тов левых частей уравнений системы (7.14), является мульмо — дальной, что обусловлено периодичностью тригонометрических выражений, входящих в ее состав. Для поиска глобального экс­тремума целевой функции Ф использован метод мультистарта. Для многомерной оптимизации применен модифицированный метод Хука-Дживса, который относится к методам поиска нуле­вого порядка и выгодно отличается простотой и эффективно­стью. Метод Хука-Дживса состоит из последовательности шагов исследующего поиска вокруг базисной точки (аналогично поко­ординатному спуску), за которой в случае успеха следует поиск по образцу [71].

Условием окончания поиска служило уменьшение шага до определенной величины, что соответствовало заданной точно­сти определения искомых параметров. Линейные параметры на­ходились с точностью 10-7, угловые параметры — с точностью 10 8, при этом целевая функция в среднем принимала значения Ф = 10-17. Установлено, что в большинстве случаев можно лока­лизовать глобальный минимум с помощью правильного выбора начального приближения. Таким начальным приближением слу­жит решение системы уравнений (7.13) при угле X = 0. Исполь­зование данного приема позволяет избежать нахождения всех экстремумов мульмодальной целевой функции и существенно повысить эффективность решения.

В качестве примера рассчитаем формообразующую траек­торию для трех типов валков, представленных в табл. 7.1. Тео­ретически точные валки для изготовления бомбинированной по­верхности имеют идентичный симметричный профиль, валки для изготовления цилиндрической поверхности — одинаковый несимметричный профиль и развернуты в противоположных направлениях, в результате они симметричны относительно плоскости дВ = 0.

Координаты формообразующей траектории приведены в табл. 7.2 для следующих параметров: цилиндрическая поверх­ность — r = 15 мм, X = = 1,75°, v = 71 мм; бомбинированная по­верхность — r = 10 мм, X = 1,5°, v = = 30 мм; бомбинированная поверхность, обрабатываемая на валках в форме однополостно­го гиперболоида, — r = 15 мм, X = 4,125°, v = 66 мм.

Профили валков суперфинишного станка для обработки
цилиндрической и бомбинированной поверхностей

Таблица 7.1 Валок для цилиндрической поверхности zB, мм -400 -300 -200 -100 0 100 200 300 400 R, мм 68,155 66,606 65,144 63,773 62,499 61,326 60,258 59,301 58,458 V, град 0,911 0,863 0,812 0,758 0,702 0,642 0,580 0,516 0,449 Валок для бомбинированной поверхности 2в, мм -100 -75 -50 -25 0 25 50 75 100 R, мм 23,455 25,661 27,478 28,649 29,051 28,649 27,478 25,661 23,455 V, град -2,073 -1,894 -1,395 -0,732 0 0,732 1,395 1,894 2,073 Валок в форме однополостного гиперболоида 2в, мм -400 -300 -200 -100 0 100 200 300 400 R, мм 63,684 63,169 62,798 62,575 62,500 62,575 62,798 63,169 63,684 V, град 0,134 0,102 0,068 0,034 0 -0,034 -0,068 -0,102 -0,134

Поверхности валков для обработки цилиндрических и бом — бинированных поверхностей получены на основе строгого про­филирования, поэтому они обеспечивают теоретическую траек­торию с известными параметрами и используются как тестовые. Исследования показали, что валки в форме однополостного ги­перболоида для исходно цилиндрической заготовки создают траекторию, близкую к дуге окружности.

Таблица 7.2 Расчетные координаты формообразующей траектории Обработка цилиндрической поверхности Zb, мм -100 -300 -200 -100 0 100 200 300 400 а, мкм -0,53 -0,44 -0,06 -0,12 0 0,12 0,06 0,44 0,53 АЬ, мкм 0,8 0,9 0,12 0 0,8 0 0,12 0,9 0,8 Обработка бомбинированной поверхности Zb, мм -100 -75 -50 -25 0 25 50 75 100 а, мм 1,238 1,207 0,933 0,505 0 -0,505 -0,933 -1,207 -1,238 Ь, мм 14,631 19,201 22,424 24,345 24,983 24,345 22,424 19,201 14,631 ос, град 0,312 0,389 0,869 1,154 1,249 1,154 0,869 0,389 0,312 3, град 12,086 8,944 5,936 2,963 0 -2,963 -5,936 -8,944 -12,086 Обработка на валках в форме однополостного гиперболоида Zb, мм -100 -300 -200 -100 0 100 200 300 400 а, мм 12,689 11,166 8,229 4,353 0 -1,353 -8,229 -11,166 -12,689 Ь, мм 29,148 34,197 37,802 39,992 40,729 39,992 37,802 34,197 29,148 ос, град 0,336 1,327 1,995 2,401 2,537 2,401 1,995 1,327 0,336 3, град 3,983 2,462 1,658 0,84 0 -0,84 -1,658 -2,462 -3,983

 

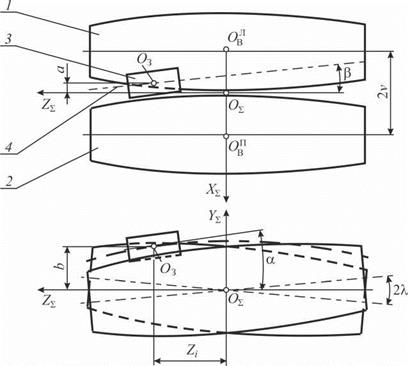
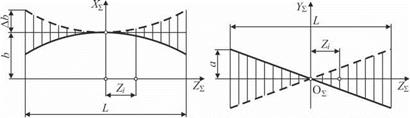
Наиболее актуальными параметрами для прямолинейной траектории при обработке цилиндрических поверхностей явля­ются высота траектории bmax и отклонения в проекциях на вер­тикальную АЬ и горизонтальную Аа плоскости станка. Для ду­говой траектории при обработке бомбинированных поверхно­стей важны радиус траектории R0, вертикальное положение ду­ги, заданное координатой bmax, и отклонения в горизонтальной плоскости Аа (рис. 7.3). На основе табл. 7.2 рассчитаны пара­метры формообразующих траекторий для новой модели, извест­ной модели, а также фактические значениями параметров, кото­рые приведены в табл. 7.3.

Рис. 7.3. Параметры пространственной формообразующей траектории: 1 — левый валок; 2 — правый валок; 3 — заготовка; 4 — формообразующая траектория

Анализ табл. 7.3 показал, что новая математическая модель обеспечивает более высокую точность расчета формообразую­щей траектории, чем предшествующая. Так, для цилиндриче­ской поверхности теоретическая высота траектории составляет ЬТтах = 31,068 мм, полученная по расчету Ьтах = 31,054 мм, а от­клонения АЬ и а не превышают 1 мкм. Для бомбинированной поверхности теоретические радиус дуги окружности RT0 = = 500 мм и высота ЬТтах = 25 мм, полученные по расчету R0 = = 488 мм, bmax = 24,983 мм. Рассчитанные значения углов пово­рота заготовки в вертикальной и горизонтальной плоскости со­ответствуют форме траектории (ось заготовки приближенно яв­ляется касательной к траектории).

Один из наиболее значимых выводов, определяющих прак­тическую ценность разработанной модели, — обоснование воз­можности получения дуговой траектории для цилиндрической заготовки на валках типа однополостных гиперболоидов. При­менение такой технологически простой формы валков делает их универсальными, что особенно актуально в условиях подшип­никовых заводов.

Параметры формообразующей траектории

Таблица 7.3 Расчетная модель Цилиндрическая поверхность Бомбинированная поверхность Ьтах, мм АЬmax, мкм Ааmax, мкм Ьтах, мм Ааmax, мм R0, мм Известная модель 31,031 0,65 0,92 24,97 1,27 480,6 Новая модель 31,054 0,66 0,53 24,98 1,24 488,4 Фактическая 31,068 0 0 25,0 0 500,0

Наладка бесцентровых суперфинишных станков для об­работки цилиндрических поверхностей

В условиях многономенклатурного производства (напри­мер, в подшипниковой промышленности) станок с одним и тем же валковым устройством используют для обработки цилинд­рических деталей различных диаметров d. При этом за номи­нальный диаметр dН детали при профилировании валков прини­мают среднее значение из диапазона обработки [24].

Анализ формообразующей траектории показал, что при по­стоянных валках при обработке заготовок различных диаметров имеют место отклонения, величина которых во много раз пре­восходит допуск на диаметр детали. Поэтому необходима ми­нимизация данных отклонений за счет подналадки суперфи­нишного станка. Известная методика [24], основанная на обоб­щении экспериментальных данных, позволяет установить каче­ственный характер влияния параметров наладки, но не может обеспечить высокой точности расчета. Строгое решение указан­ной задачи возможно только в рамках новой модели, представ­ленной уравнениями (7.13).

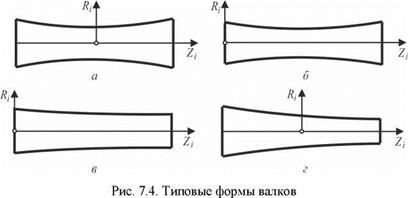
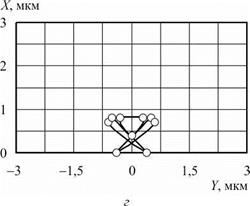
Рассмотрим следующие типы валков для обработки цилин­дрических поверхностей (рис. 7.4): а — однополостный гипербо­лоид (станки фирмы Mikrosa); б — близкий к гиперболоиду с симметричным профилем [39]; в — близкий к гиперболоиду с не­симметричным профилем [24] (отечественные станки); г — ква­зигиперболоид [45].

Установим характер погрешностей, возникающих при обра­ботке заготовок на рассмотренных типах валков. Несмотря на то, что не все из них рассчитаны на основе строгих соотноше­ний, в ряде случаев их применение рационально. Во-первых, валки в виде однополостных гиперболоидов имеют простую геометрическую форму (что, однако, не гарантирует простоту изготовления методом шлифования) и меньшие габаритные размеры по сравнению с другими. Во-вторых, целесообразность применения того или иного типа валков для обработки широко­го диапазона размеров заготовок окончательно не получила тео­ретического обоснования.

В табл. 7.4 представлены результаты расчета профиля дан­ных валков по авторским формулам [24, 39] для X = 1,75°; r = 15 мм при рекомендуемых параметрах наладки станка: а) X = 1,87°, v = 73,28 мм; б) v = 73,055 мм; в) v = 70,469 мм; г) v = 71,0 мм.

Типовые профили валков бесцентровых
суперфинишных станков

Таблица 7.4 Z, мм -400 -300 -200 -100 0 100 200 300 400 R, мм а 63,684 63,169 62,798 62,575 62,500 62,575 62,798 63,169 63,684 б 63,578 63,109 62,772 62,568 62,500 62,568 62,772 63,109 63,578 в 64,993 63,594 62,290 61,087 59,988 59,000 58,126 57,370 56,736 г 66,964 65,698 64,528 63,461 62,499 61,647 60,909 60,286 59,785

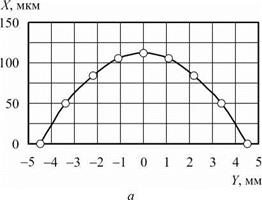
Результаты анализа формообразующей траектории даны на рис. 7.5, где показаны отклонения от номинальной прямой в проекциях на вертикальную и горизонтальную плоскости станка. Расчетные данные приведены для 9 сечений, соответст­вующих табл. 7.4, причем в следующих единицах измерения: по оси ординат — в мкм, а по оси абсцисс для вариантов а и б — в мм, а для в и г — в мкм.

X, мкм З

			д	f
			/
			о—	—о

в

Рис. 7.5. Формообразующая траектория
для различных типов валков

Рис. 7.5. Окончание

Анализ отклонений формообразующей траектории для раз­личных типов валков позволил сделать следующие выводы:

• валки в виде однополостных гиперболоидов создают значительные отклонения формообразующей траектории в вер­тикальной и горизонтальной плоскостях станка, что приводит к возникновению погрешности профиля продольного сечения в виде бочкообразности, поэтому данный тип валков рекоменду­ют использовать только при оптимальных наладках;

• валки, близкие к однополостному гиперболоиду с сим­метричным и несимметричным профилями, обеспечивают от­клонения в вертикальной плоскости станка в пределах 3-5 мкм, подобную погрешность можно считать приемлемой, однако при этом у валков с симметричным профилем отклонения формооб­разующей траектории в горизонтальной плоскости достигают 9 мм, что приводит к несимметричному расположению загото­вок относительно шлифовальных брусков;

• валки, спрофилированные по авторскому методу, обес­печивают погрешность формообразующей траектории в преде­лах 1 мкм, которая обусловлена в первую очередь округлением до 1 мкм исходных значений радиуса валков при их задании в модели.

Рассмотрим отклонения формообразующей траектории, воз­никающие при обработке заготовок различных диаметров на од­ном валковом устройстве. При анализе известные профили валков разделены на две группы: симметричные (рис. 7.4, а, б) и несим­метричные (рис. 7.4, в, г). Анализировали валки, исходно рассчи­танные для диаметра 0 30 мм. Моделировалась обработка загото­вок с диаметрами 0 24 мм и 0 40 мм. Результаты отклонений формообразующей траектории представлены в табл. 7.5, 7.6.

Отклонения формообразующей траектории при d < dH

Таблица 7.5 Z, мм -400 -300 -200 -100 0 100 200 300 400 <г <1 а 0,0564 0,0369 0,0158 0,0081 0 0,0081 0,0158 0,0369 0,0564 б 0,2140 0,1260 0,0604 0,0150 0 0,0150 0,0604 0,1260 0,2140 в 0 0,1308 0,2213 0,2754 0,2901 0,2754 0,2213 0,1308 0 г 0 0,064 0,1086 0,1354 0,1448 0,1354 0,1086 0,064 0 <1 а 2,40 1,80 1,20 0,60 0 -0,60 -1,20 -1,80 -2,40 б 2,50 1,80 1,20 0,60 0 -0,60 -1,20 -1,80 -2,50 в -1,77 -1,31 -0,86 -0,43 0 0,43 0,86 1,31 1,77 г -1,28 -0,95 -0,63 -0,31 0 0,31 0,63 0,95 1,28

Отклонения формообразующей траектории при d > dH

Таблица 7.6 Z, мм -400 -300 -200 -100 0 100 200 300 400 S S <г <1 а 0 0,1099 0,1958 0,2375 0,2493 0,2375 0,1958 0,1099 0 б 0 0,0645 0,1106 0,1361 0,1450 0,1361 0,1106 0,0645 0 в 0,0702 0,0406 0,0186 0,0057 0 0,0057 0,0186 0,0406 0,0702 г 0,0671 0,0379 0,0167 0,0042 0 0,0167 0,0042 0,0379 0,0671 S S <1 а -6,70 -5,05 -3,40 -1,70 0 1,70 3,40 5,05 6,70 б -6,40 -4,80 -3,20 -1,60 0 1,60 3,20 4,80 6,40 в 1,84 1,37 0,90 0,45 0 -0,45 -0,90 -1,37 -1,84 г 1,55 1,16 0,77 0,39 0 -0,39 -0,77 -1,16 -1,55

Характер отклонений формообразующей траектории в проек­циях на вертикальную и горизонтальную плоскости станка показан на рис. 7.6, где для несимметричных валков сплошной линией изо­бражены отклонения для диаметра заготовки больше номинально­го и штриховой линией — для диаметра меньше номинального. У симметричных валков показаны: сплошная линия — для обраба­тываемого диаметра меньше номинального и штриховая линия — для диаметра больше номинального.

Рис. 7.6. Отклонения формообразующей траектории в зависимости от диаметра обрабатываемых заготовок

Отклонения формообразующей траектории в горизонтальной Аа и в вертикальной АЬ плоскостях представляют собой макси­мальную разность номинальных и расчетных значений параметров а и Ь соответственно. При этом отклонение АЬ = bmax — bmn, откло­нение Аа = а, так как номинальное значение а равно нулю.

Установлено, что если диаметр заготовки меньше номи­нального d < dH, то траектория при симметричных валках имеет вогнутый вид, а при несимметричных — выпуклый. Если диа­метр заготовки больше номинального d > dH, то при симметрич­ных валках траектория выпуклая, а при несимметричных — во­гнутая. Отклонения траектории в вертикальной плоскости сим­метричны относительно плоскости Z = 0. Отклонения траекто­рии в горизонтальной плоскости с достаточной точностью ап­проксимируются прямой, симметричной относительно точки 0^.

Отклонения в вертикальной плоскости непосредственно влияют на профиль продольного сечения деталей, а отклонения в горизонтальной плоскости, не выходящие за ширину инстру­мента, мало сказываются на точности обработки. Таким обра­зом, в первую очередь требуется минимизация отклонений фор­мообразующей траектории в вертикальной плоскости.

Для оптимизации наладочных параметров X и v суперфи­нишного станка можно использовать целевую функцию Q(X, v), модифицированную из условной целевой функции G(X, v) с уче­том конструктивных, кинематических и силовых ограничений:

Q(X, v) = G(X, v) + r X(1/V,(X, v)), (7.15)

i=1

где V (X, v) > 0 — ограничения типа неравенств; r, — коэффициен­ты, подбираемые из требований точности и экономичности вы­числений.

Функция G(X, v) представляет собой вектор отклонений формообразующей траектории, формируемый по алгоритму как разность максимальных и минимальных отклонений траектории в вертикальной плоскости:

G (Ф X v) = {bmax — bmin } ^ min,

где Ф — целевая функция, определяемая по выражению (7.14).

В выражении (7.15) конструктивные и кинематические ог­раничения имеют явный вид: X1 < X < X2, vi < v < v2, а силовые ограничения имеют неявный вид V (X, v) > 0 и определяются из граничного условия. Нахождение взаимосвязи параметров на­ладки X, v и углов контакта ФЛ, ФП заготовки с валками осущест­вляют на основе решения системы уравнений (7.13).

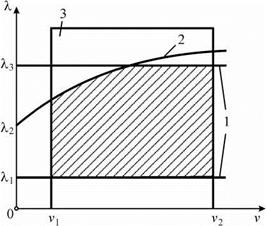
Характерная область работоспособности в координатах па­раметров наладки X, v показана на рис. 7.7. Установлено, что в области работоспособности целевая функция всегда имеет толь­ко один минимум.

В качестве формального метода оптимизации использован модифицированный метод Хука-Дживса, хорошо зарекомендо­вавший себя при выпуклой области работоспособности и вы­пуклой целевой функции. Поскольку используется метод внут­ренней точки, начальное приближение всегда выбирается в до­пустимой точке.

Рис. 7.7. Область работоспособности при наладке бесцентровых суперфинишных станков

Для приведенного примера (см. табл. 7.5, 7.6) была прове­дена оптимизация межосевого расстояния v и угла перекрещи­вания X валков, результаты которой даны в табл. 7.7. Оптимиза­ция выполнялась как по каждому из параметров, так и одновре­менно по обоим параметрам. Обозначения форм валков в табл. 7.7 соответствуют ранее введенным.

Таблица 7.7

Результаты оптимизации параметров v и X

Деталь	r = 12 мм	r = 20 мм
Парамет	ры	v	X	v, X	v	X	v, X
Результаты оптимизации		а	72,95	73,28	73,50	76,80	73,28	79,00
б	71,55	73,06	73,06	75,35	73,06	76,00
в	67,00	70,47	69,00	67,15	70,47	71,50
г	67,50	71,00	68,20	66,90	71,00	73,00
и &	а	1,87	1,879	1,881	1,87	1,785	1,923
б	1,75	1,786	1,785	1,75	1,697	1,765
в	1,75	1,700	1,714	1,75	1,779	1,787
г	1,75	1,711	1,722	1,75	1,780	1,791

Выявлено, что отклонения формообразующей траектории в вертикальной плоскости в большинстве случаев удается мини­мизировать до требуемой величины. Однако отклонения в гори­зонтальной плоскости в меньшей степени поддаются управле­нию, а в ряде случаев минимизация отклонения в вертикальной плоскости приводит к увеличению отклонений в горизонталь­ной плоскости. Поэтому необходима коррекция положения шлифовальных брусков относительно траектории движения за­готовок.

Проведенные эксперименты по оптимизации формообра­зующей траектории позволили сделать следующие выводы:

• оптимальная наладка суперфинишного станка обеспечи­вает минимизацию отклонений формообразующей траектории для деталей: d < dH при увеличении X или уменьшении v (сим­метричные валки) и при уменьшении X и v (несимметричные валки); d > dH — при уменьшении X или увеличении v (симмет­ричные валки), при увеличении X или уменьшении v (несиммет­ричные валки);

• при оптимизации параметра X отклонения траектории в горизонтальной плоскости мало изменяются, а при оптимизации параметра v — для симметричных валков увеличиваются при d < dH и уменьшаются при d > dH, для несимметричных валков — при d < dH уменьшаются и при d > dH увеличиваются;

• отклонения формообразующей траектории в горизон­тальной плоскости при оптимизации снижаются незначительно, поэтому необходима коррекция относительного положения вал­кового устройства и суперфинишных станций станка;

• для несимметричных валков при оптимизации параметра v не удалось снизить отклонения в вертикальной плоскости до требуемой величины для варианта d < dH;

• при соотношении диаметров d и dH, различающемся бо­лее чем в 5 раз, не удается минимизировать отклонения формо­образующей траектории при конструктивно реализуемых налад­ках станка, что определяет диапазон рационального использова­ния валков одного профиля.

При наладке валкового устройства станка актуальной зада­чей является определение требуемой точности установки межо­севого расстояния и угла перекрещивания валков суперфиниш­ного станка. Без решения этой задачи рекомендации по опти­мальной наладке станка утрачивают свою эффективность.

На рис. 7.8 представлены характерные результаты влияния точности геометрической наладки на отклонения формообра­зующей траектории в проекциях на вертикальную и горизон­тальную плоскости станка, рассчитанные для трех вариантов: v = 73,0 мм, X = 1,75°, r = 15 мм; v = 71,0 мм, X = 1,75°, r = 18 мм; v = 71,0 мм, X = 1,6°, r = 15 мм для валков длиной 800 мм с осе­вым профилем, рассчитанным по авторской методике.

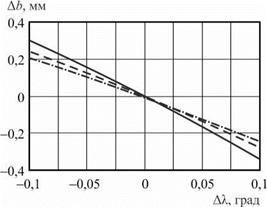
Анализ графиков на рис. 7.8 показал, что погрешность наладки межосевого расстояния v влияет на отклонения формообразующей траектории в вертикальной плоскости в диапазоне ±0,1 мм крайне слабо. Характер полученных кривых (рис. 7.8, а) во многом объяс­няется округлением при исходном задании радиусов валков. От­клонения в горизонтальной плоскости (рис. 7.8, б) близки к линей­ным и не превышают погрешности наладки самого межосевого расстояния. Погрешность наладки угла перекрещивания X вызыва­ет значительные отклонения формообразующей траектории в вер­тикальной плоскости (рис. 7.8, в). При этом ветвь кривой, соответ­ствующая положительному значению AX, имеет больший угол на­клона. Отрицательные значения параметра Ab означают, что траек­тория имеет выпуклый вид.

Характерно, что отклонения в горизонтальной плоскости линейны и симметричны относительно номинального значения наладки (начала системы координат); диапазон изменения от­клонений в зависимости от погрешности наладки межосевого расстояния и угла перекрещивания валков достаточно узкий и слабо зависит от номинальных наладочных параметров и диа­метра детали (рис. 7.8, б, г).

Аналогичные результаты были получены для других форм валков. Отличие состоит в том, что для не строго рассчитанных валков номинальные отклонения формообразующей траектории не равны нулю.

г

Рис. 7.8. Окончание

Проведенные эксперименты позволили сделать следующие выводы:

• наибольшее влияние на отклонения формообразующей траектории оказывает угол X перекрещивания валков;

• погрешность наладки межосевого расстояния v валков в диапазоне +(0,05…0,1) мм приводит к незначительным отклоне­ниям формообразующей траектории в вертикальной плоскости (в пределах 1 мкм);

• погрешность наладки угла X перекрещивания валков в диапазоне ±(0,05…0,1)° вызывает отклонения формообразую­щей траектории в пределах 0,1-0,4 мм;

• зависимости отклонений формообразующей траектории в вертикальной и горизонтальной плоскостях от погрешности наладки угла перекрещивания и межосевого расстояния валков близки к линейным.

Установку межосевого расстояния на станке производят с помощью калибра, закрепляемого в специально предусмотрен­ном отверстии на валковом устройстве в точке перекрещивания осей валков. Угол перекрещивания осей валков выставляют от­дельно для каждого валка с использованием микрометрических винтов и плиток 2-го класса точности.

Таким образом, рекомендуемая точность геометрической на­ладки бесцентрового суперфинишного станка составляет: по углу перекрещивания — AX = 10", по межосевому расстоянию — Av = = 0,1 мм. Для сравнения точность наладки данных параметров, ре­комендуемая отечественными производителями суперфинишных станков [24], составляет 30" и 0,05 мм соответственно.

Наладка бесцентровых суперфинишных станков для об­работки бомбинированных поверхностей

Один из наиболее сложных случаев при бесцентровом су­перфинишировании — обработка бомбинированных поверхно­стей. Для создания бомбинированной поверхности на заготовке формообразующая траектория должна быть дугой окружности определенного радиуса, согласованного по величине с радиусом бомбины. Традиционно обработку бомбинированных поверхно­стей осуществляют на суперфинишных станках с валковыми устройствами, включающими два валка со сложным профилем осевого сечения. Изготовление таких валков требует специали­зированных многокоординатных шлифовальных станков, из-за чего стоимость валкового устройства достигает 40 % от всего суперфинишного станка.

Исследования показали, что на суперфинишном станке с валками типа однополостных гиперболоидов траектория движе­ния цилиндрических заготовок приближенно соответствует дуге окружности в зависимости от геометрической наладки станка. Указанный факт стал основанием для изучения возможности обработки бомбинированных поверхностей на валках, имеющих форму однополостных гиперболоидов.

Установим формообразующую траекторию для цилиндри­ческих заготовок на валках типа однополостных гиперболоидов и оценим ее отклонение от дуги окружности, а также исследуем влияние параметров наладки на радиус дуги аппроксимирую­щей окружности. Для этого вначале проведем численный экспе­римент, в котором рассчитаем координаты формообразующей траектории по формулам (7.13), (7.14) для различных сочетаний размеров заготовки, валков и параметров наладки станка.

В табл. 7.8 представлены некоторые результаты численного эксперимента для следующих исходных данных: угол образую­щей однополостного гиперболоида у = 1°; минимальный радиус валка R = 60 мм, межосевое расстояние валков 2v = 124 мм. Ис­ходно цилиндрические заготовки имеют радиусы r = 10, 20 мм. Точность решения системы (7.13) задана значением целевой функции Ф < 10-6, вычисляемой по выражению (7.14).

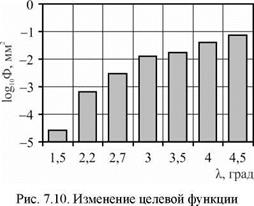
Аппроксимация полученных координат формообразующей траектории (рис. 7.9) проведена по трем точкам и методом наи­меньших квадратов. Для определения инвариантности наладоч­ных параметров расчет выполнен для четырех длин валков (табл. 7.9). Также на рис. 7.10 показано изменение целевой функции Ф для заготовки r = 20 мм (для лучшего масштаба гра­фик построен в логарифмической системе координат).

Радиус Ri аппроксимирующей дуги окружности по трем точкам рассчитан по формуле

где Ab, = bmax — Ь,.

Координаты формообразующей траектории
при суперфинишировании бомбинированных поверхностей
на валках типа однополостных гиперболоидов

град	2, мм	-400	-300	-200	-100	0	100 200 300	400
r = 10 мм
1,5		31,266	31,816	32,210	32,448	32,527	32,448	32,210	31,816	31,266
1,7	30,667	31,482	32,066	32,418	32,536	32,418	32,066	31,482	30,667
2,2	28,828	30,464	31,629	32,329	32,562	32,329	31,629	30,464	28,828
2,5	27,483	29,726	31,313	32,264	32,581	32,264	31,313	29,726	27,483
2,7	26,478	29,179	31,080	32,217	32,595	32,217	31,080	29,179	26,478
3,0	24,795	28,274	30,696	32,138	32,618	32,138	30,696	28,274	24,795
	r = 20 мм
1,5	49,439	49,934	50,291	50,507	50,580	50,507	50,291	49,934	49,439
2,2	47,463	48,817	49,804	50,404	50,606	50,404	49,804	48,817	47,463
2,7	45,636	47,777	49,347	50,307	50,631	50,307	49,347	47,777	45,636
3,0	44,379	47,058	48,985	50,240	50,648	50,240	48,985	47,058	44,379
3,5	42,031	45,709	48,431	50,112	50,681	50,112	48,431	45,709	42,031
4,0	39,376	44,180	47,749	49,965	50,719	49,965	47,749	44,180	39,376
4,5	36,408	42,475	46,984	49,800	50,761	49,800	46,984	42,475	36,408

Рис. 7.9. Схема аппроксимации траектории

Радиус R2 аппроксимирующей дуги окружности методом наименьших квадратов найден на основе минимизации функ­ционала F:

F = X (bi R — Zf — h)2 ^ min,

i=1

где h — вертикальная координата центра дуги окружности.

Таблица 7.9

Радиусы аппроксимирующих окружностей
формообразующей траектории при обработке
бомбинированных поверхностей

X, град	Z, мм Г-100; 1001 Г-200; 2001	Г-300; 3001	О о "-|- о о "-|-
r = 10 мм
1,5	R1, м	63,052	63,044	63,279	63,437
R2, м	63,052	63,022	63,292	63,457
1,7	Ri, м	42,600	42,610	42,732	42,818
R2, м	42,600	42,611	42,741	42,829
2,2	R1, м	21,434	21,434	21,450	21,429
R2, м	21,434	21,435	21,451	21,431
2,5	R1, м	15,782	15,776	15,761	15,697
R2, м	15,782	15,775	15,760	15,697
2,7	R1, м	13,214	13,203	13,174	13,082
R2, м	13,214	13,201	13,171	13,082
3,0	R1, м	10,425	10,409	10,361	10,230
R2, м	10,425	10,406	10,356	10,229

X, град	Z, мм	т о о о о	Г-200; 2001	Г-300; 3001	О О "-|- © о
r = 20 мм
1,5	Ri, м	69,137	69,255	69,673	70,111
R2, м	69,137	69,271	69,711	70,148
2,2	R1, м	24,808	24,932	25,159	25,452
R2, м	24,808	24,949	25,184	25,472
2,7	R1, м	15,467	15,580	15,771	16,018
R2, м	15,467	15,596	15,793	16,036
3,0	R1, м	12,251	12,026	12,537	12,764
R2, м	12,251	12,051	12,558	12,807
3,5	R1, м	8,790	8,893	9,054	9,253
R2, м	8,790	8,907	9,073	9,269
4,0	R1, м	6,638	6,737	6,886	7,059
R2, м	6,638	6,751	6,904	7,074
4,5	R1, м	5,201	5,297	5,435	5,581
R2, м	5,201	5,311	5,452	5,596

Выявлено, что формообразующая траектория отличается от геометрически точной окружности, однако отклонения невели­ки. Расхождения между радиусами R1 и R2 при аппроксимации по трем точкам и методом наименьших квадратов находятся в пределах 0,5 %. Поэтому на практике расчет достаточно вести по трем точкам траектории. Погрешность аппроксимации моно­тонно увеличивается при уменьшении радиуса дуги. Макси­мальная погрешность аппроксимации соответствует наиболь­шей длине валков. Анализ показал, что увеличение высоты b траектории в вертикальной плоскости приводит к уменьшению радиуса R2 аппроксимирующей окружности. При этом отклоне­ния траектории от окружности также увеличиваются. Характе­рен рост кривизны фактической формообразующей траектории по сравнению с кривизной аппроксимирующей окружности.

Оптимизацию наладочных параметров X и v суперфинишно­го станка, позволяющую получить заданную величину b и, как следствие, требуемый радиус R2 формообразующей траектории, можно выполнять как одновременно по обоим указанным пара­метрам, так и по каждому из них в отдельности. Увеличению

высоты b при прочих равных условиях способствуют: увеличе­ние угла перекрещивания осей и длины валков, радиуса заготов­ки, уменьшение межосевого расстояния валков. Угол перекре­щивания осей валков всегда должен быть больше, чем угол об­разующей однополостного гиперболоида. Однако при значи­тельном увеличении угла X возможна ситуация, когда заготовка располагается ниже точки перекрещивания валков и фактически обработка не возможна.

Рассмотрение валков различной длины при одной наладке станка показало, что полученные радиусы аппроксимирующей окружности во всех случаях близки. Например, для заготовки r = 10 мм отклонения находятся в пределах 2 %, а для заготовки r = 20 мм — в пределах 7 %. Поэтому можно сделать вывод о том, что заданная наладка суперфинишного станка обеспечивает определенный радиус дуги окружности вне зависимости от дли­ны валков.

Общие рекомендации по наладке суперфинишного станка при обработке бомбинированных поверхностей можно сформу­лировать следующим образом. Вначале выбирают минимальное межосевое расстояние валков, удовлетворяющее условию сило­вого замыкания контакта. Затем устанавливают угол перекре­щивания осей валков, ограниченный решением геометрической задачи и конструктивными особенностями станка. В последнюю очередь назначают скорость вращения валков и частоту осцил­ляции шлифовальных брусков станка.

Параметры наладки и формообразующей траектории
при суперфинишировании бомбинированных поверхностей

Таблица 7.10 г, мм 5 10 15 20 25 30 50 v, мм 60,1 X, град 2,4 3,5 4,3 5,0 5,6 6,1 8,0 Rmin, м 13,799 7,656 5,687 4,549 3,841 3,376 2,194

При обработке бомбинированных поверхностей на валках в форме однополостных гиперболоидов затруднительно получение малых радиусов траектории движения и, соответственно, радиусов профиля заготовки. Результаты расчета наладок, обеспечивающих минимальные радиусы Rr„,„ дуговой траектории при обработке за­готовок различных диаметров, приведены в табл. 7.10. Из нее вид­но, что с увеличением диаметра заготовок диапазон минимальных радиусов формообразующей траектории расширяется.