Отклонения формы заготовок в партии носят стохастический характер. При статистическом моделировании методом Монте-Карло требуется знание законов и параметров распределений составляющих погрешностей, а также наличия корреляционных связей между ними. Подробные справочные данные по законам распределения погрешностей формы деталей при различных методах обработки в известной литературе отсутствуют. Проведены экспериментальные исследования в условиях ОАО «Саратовский подшипниковый завод». В качестве объектов были взяты по две партии из 50 заготовок колец подшипников при шлифовании на неподвижных опорах и 50 валиков (поршневых пальцев) при бесцентровом шлифовании и суперфинишировании с продольной подачей.
Задача идентификации распределений решалась на основе положений теории вероятностей и математической статистики. Идентификацию эмпирической плотности распределения можно реализовать с помощью различных программных продуктов для статистического анализа данных [69]. Однако основной недостаток известных пакетов программ связан с ограниченным набором аналитических распределений (обычно 7-15 для непрерывных распределений). Поэтому разработана программа для идентификации гистограмм случайных величин. Составленная база теоретических законов распределений включает 30 известных классов непрерывных одномодальных распределений, получивших наибольшее распространение в технике: распределения Вейбулла, Стьюдента, Фишера, Парето, Пирсона, Джонсона, логистическое, логарифмически нормальное, бета-, гамма-, z-распределения и др.
Идентификация распределения проводилась в следующей последовательности:
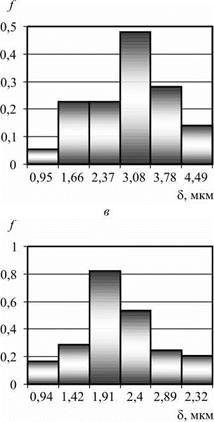
1) по выборке данных строились гистограммы отклонения от круглости, профиля продольного сечения, амплитуд и начальных фаз гармоник поперечного сечения заготовок;
2) вычислялись оценки главных моментов распределений, коэффициенты асимметрии, эксцесса;
3) на основе анализа формы гистограмм, значений моментов и графика в координатах в и р2 выдвигались первоначальные гипотезы о теоретической функции распределения;
4) для выбранных распределений и классов распределений рассчитывались оценки параметров распределения методами моментов и максимального правдоподобия;
5) проверялись сложные статистические гипотезы по критерию согласия на отсутствие различия между теоретическим и эмпирическим распределениями;
6) для распределений, удовлетворяющих критерию согласия, уточнялись параметры по методу наименьших квадратов (если первоначально они рассчитывались по методу моментов);
7) выбирался наилучший закон распределения по наименьшему значению целевой функции в методе наименьших квадратов.
 |
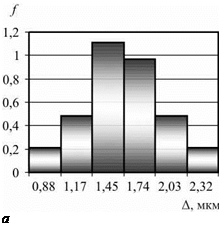Гистограммы отклонения от круглости и профиля продольного сечения после бесцентрового шлифования и суперфиниширования с продольной подачей представлены на рис. 6.13.
/
1,2
1
0,8
0,6
0,4
0,2
0
А, мкм б
|
Рис. 6.13. Окончание г |
В результате идентификации по рассмотренной методике окончательно установлено:
• отклонение от круглости распределено по нормальному или логарифмически нормальному закону;
• отклонение от профиля продольного сечения распределено по нормальному закону;
• амплитуды гармоник поперечного профиля соответствуют бета-распределению (распределению Пирсона второго типа);
• начальные фазы гармоник поперечного профиля соответствуют равномерному распределению.
Для проверки склонности методов бесцентровой абразивной обработки к геометрическому наследованию отклонений формы проведены экспериментальные исследования и выполнен корреляционный анализ.
Рассчитанный коэффициент корреляции при бесцентровом суперфинишировании составил для отклонения от круглости 0,878; для отклонения продольного профиля 0,857. На основе полученных результатов о надежности корреляционных связей, а также нормальности распределения отклонения от круглости и профиля продольного сечения можно выполнить регрессионный анализ. Полученные регрессионные уравнения имеют вид:
• для отклонения от круглости при шлифовании Д2 = = 0,174Ді + 0,694; при суперфинишировании Д2 = 0,257Ді + + 0,118;
• для отклонения профиля продольного сечения 52 = = 0,5198і + 0,469.
Для статистического моделирования необходимы сведения о корреляционных связях между отдельными составляющими погрешности. Поскольку начальные фазы распределены по закону равной вероятности, корреляционный анализ требуется только для амплитуд гармоник. Коэффициент корреляции представляет собой состоятельную оценку независимо от закона распределения случайных величин.
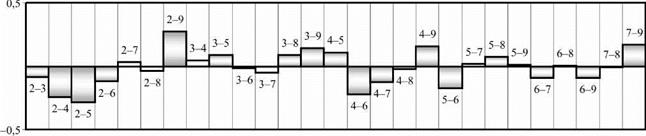
Рассчитан коэффициент корреляции для парных сочетаний амплитуд гармоник со 2 по 9-ю, так как они имеют наибольшие абсолютные значения. Результаты приведены на рис. 6.14 для шлифования с продольной подачей, предшествующей операции суперфиниширования.
Таким образом, при статистическом моделировании необходимо учитывать корреляцию между 2-й и 5-й гармониками при шлифовании с продольной подачей и между 2-й и 3-й, 2-й и 4-й, 2-й и 8-й, 3-й и 4-й, 3-й и 5-й, 3-й и 8-й, 3-й и 9-й, 4-й и 8-й, 4-й
 |
|
|
и 9-й, 7-й и 9-й гармониками при шлифовании с поперечной подачей. Анализ показал, что значимую корреляцию имеют в основном четные гармоники, например 2-я и 4-я, 2-я и 8-я, а также нечетные 3-я и 5-я, 3-я и 9-я, 7-я и 9-я. Из этого следует вывод о наличии в технологической системе периодически действующих факторов. Одним из таких факторов может быть переменная жесткость самой детали, имеющей три асимметричных отверстия. Гармоники 2, 3, 4 и 8 образуют группу взаимосвязанных коррелированных параметров, коэффициент корреляции для их сочетаний изменяется от 0,549 до 0,68. Поэтому при статистическом анализе целесообразно принять единый коэффициент корреляции в виде среднеарифметического значения 0,588.
Для проверки рекомендаций по оптимальной наладке бесцентрового суперфинишного станка модели SZZ-3 по углу перекрещивания 2Х и межосевому расстоянию 2v валков выполнены исследования на основе экстремального эксперимента. Целью являлся поиск оптимальной наладки станка, удовлетворяющей технологическим возможностям оборудования, при которой отклонения от круглости и профиля продольного сечения заготовок будут минимальны. В качестве метода исследования применен метод движения к экстремуму Бокса-Уилсона. Функция отклика задана в виде отношения исходных погрешностей геометрической формы к полученным после суперфиниширования. Указанные отклонения рассматривались отдельно.
Метод Бокса-Уилсона состоит из следующих этапов:
• постановка задачи, выбор откликов и факторов, выбор области эксперимента;
• выбор подобласти линейного приближения;
• выбор модели и плана эксперимента;
• обработка результатов эксперимента;
• интерпретация уравнения регрессии;
• принятие решений после исследования регрессии;
• определение градиента и проведение опытов вдоль этого направления;
• принятие решений после движения по градиенту.
Методом Бокса-Уилсона можно оптимизировать только один отклик, остальные отклики будут рассматриваться как ограничения. В процессе движения по градиенту дополнительные отклики играют роль контролирующих параметров. Движение прекращается при выходе любого из откликов за область допустимых значений или при достижении экстремума главного отклика.
За нулевой уровень приняты стандартные наладки станка, приведенные в руководстве по эксплуатации суперфинишного станка для обработки роликов 016: X = 1,87° и v = 73,28 мм. При стандартных наладках достигнуты следующие значения: отклонение от круглости уд = 1,1 и отклонение профиля продольного сечения У5 = 0,8.
Исходя из теоретических предпосылок, считаем, что поверхность отклика близка к линейной. Точность фиксирования параметров — средняя, поэтому выбирается средний интервал варьирования по всем параметрам — 10 %. Однако по параметру v эти значения выходят за допустимые пределы и не реализуются на станке для данного диаметра заготовки, поэтому диапазон варьирования по межосевому расстоянию уменьшен.
Стратегия метода предполагает, что в выбранной подобласти неизвестную поверхность отклика можно приблизить уравнением регрессии первой степени:
МУ(ХЬ Х2) = во + вх + Р2Х2 + вХХ
где Хі — межосевое расстояние валков; Х2 — угол перекрещивания осей валков.
Для уравнений первого порядка разработаны точные факторные планы. В них все факторы меняются на двух уровнях — верхнем и нижнем. Планы представляют собой перебор всех комбинаций уровней факторов. В данном случае — ПФЭ 22 обладает свойствами ортогональности и рототабельности. План эксперимента и результаты представлены в табл. 6.5, 6.6.
Для оценки значимости каждого коэффициента вычислим оценку его дисперсии:
s2
‘"’воспр
Nn
|
Таблица 6.5 План и результаты двухфакторного эксперимента
|
Коэффициенты регрессионного уравнения
|
Таблица 6.6
|
Если доверительный интервал для коэффициентов регрессии содержит ноль
I bi | < | І0,975; f2 Sbi I,
то гипотеза bt = 0 не отвергается, а соответствующий член уравнения регрессии исключается. Поскольку план ортогональный, это не влечет за собой пересчет других коэффициентов регрессии.
Таким образом, получены следующие уравнения регрессии:
Уд = 1,22 + 0,16X! -0,62X2;
у5= 1,1 — 0,31 X 2 + 0,15 Xі X 2.
Анализ полученных данных и сравнение их с теоретическими результатами позволяют сделать вывод о качественном соответствии рекомендаций по геометрической наладке бесцентровых суперфинишных станков.
Рассмотрим некоторые результаты внедрения на примере деталей поршневых пальцев 6-1НР16092Е.62, 6-1НР16115Е.62. Материал — ШХ15-В ТУ 520-2002. Термическая обработка — закалка и отпуск, твердость 60-64 HRC. Проводилась последовательная оптимальная наладка станков при бесцентровом шлифовании и суперфинишировании. Операция — окончательное шлифование цилиндрической поверхности 016-0005 в два прохода. Технические требования: непостоянство диаметра — 0,009 мм; отклонения профиля продольного сечения — 0,009 мм; шероховатость Ra = 0,63 мкм. Оборудование — станок модели SASL-200×500 (Mikrosa, Германия). Скорость шлифовального круга — 35 м/с, частота вращения ведущего круга — 71 мин-1. Коэффициент проскальзывания на ведущем круге — 0,91. Угол разворота ведущего круга — 2°. Скорость продольной подачи заготовок — 2470 мм/мин. Шлифовальный круг — 375x250x305 14А 12 СТВ, ведущий круг — 225x250x127 75А 12 1В. Операция — бесцентровое суперфиниширование цилиндрической поверхности 016-0005. Технические требования: непостоянство диаметра — 0,009 мм; отклонения профиля продольного сечения — 0,009 мм; шероховатость Ra = 0,08 мкм. Припуск на обработку (диаметр) — 0,005 мм. Оборудование — станок модели SZZ-3 (Mikrosa, Германия) имеет 8 суперфинишных станций. Число двойных ходов при давлении масла 200 Н и величине хода 2,5 мм составляет 2000 дв. х/мин. Скорость продольной подачи заготовок — 0,977 м/мин (при частоте вращения валков 80 мин-1). Угол перекрещивания осей валков — 2°47′. Давление суперфинишных станций 0,1-0,35 МПа. Шлифовальные бруски 20x10x70 64С М14 СМ2 К (2 бруска), 64С М10 СМ2 К (2 бруска), 64С М7 СМ1 К (2 бруска), 64С М10 СТБ (2 бруска). Обработку осуществляли при обильном поливе водной СОЖ.
На рис. 6.15 представлены результаты, полученные при обработке валиков, где показаны: а — среднеарифметическое значение отклонения от круглости; б — среднеарифметическое значение отклонения профиля продольного сечения; в — СКО отклонения от круглости; г — СКО отклонения профиля продольного сечения (в мкм).
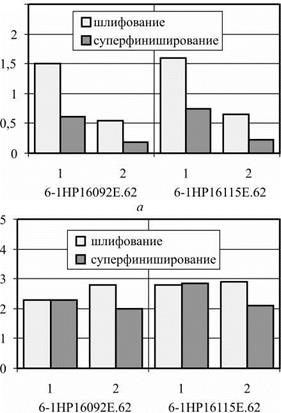Анализ данных рис. 6.15 показал, что оптимальная наладка станков и ремонт валков суперфинишного станка позволили на окончательной операции уменьшить отклонение от круглости в среднем до 2,5 раз, отклонения профиля продольного сечения в среднем на 25 % при снижении среднеквадратического отклонения до 2 раз. Итоговые результаты повышения точности объясняются тем, что при оптимальной наладке станков исходная погрешность базовой поверхности была примерно в 2 раза меньше, чем при стандартной наладке (данный фактор являлся неуп — 2,5
равляемым). Однако коэффициент исправления профиля на операции суперфиниширования на 15-25 % превысил аналогичный коэффициент, характерный для стандартной наладки станка. Также на операции бесцентрового шлифования из-за действия неучтенных факторов разброс параметров в партии был выше, чем при стандартной наладке. Однако после окончательной операции суперфиниширования удалось снизить среднеквадратическое отклонение погрешностей формы в партии.