Формообразование поперечного сечения заготовок при бесцентровом суперфинишировании

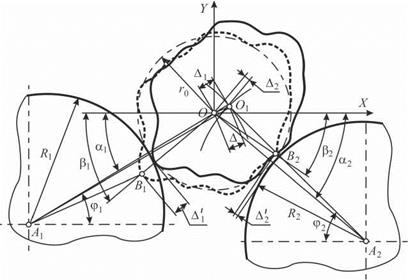
При бесцентровом суперфинишировании заготовка базиру­ется на двух валках, поперечные сечения которых представляют собой окружности радиусами R1 и R2 с центрами в точках А1 и А2 (рис. 6.5). Положение этих окружностей относительно начала системы координат (X О Y) задано углами ai и а2.

Считаем, что при базировании заготовка, описанная уравне­нием (6.7), стремится занять устойчивое положение на двух вал­ках. При этом заготовка под действием силы тяжести смещается

от номинального положения, последовательно перекатываясь по поверхностям валков. Рис. 6.5. Схема базирования заготовки при бесцентровом суперфинишировании

Установим точки контакта на основе максимума зазора, вы­раженного модулем А’ и полярным углом в:

А'(Pi) = {r(Pi +180°)- ri(Pi)} ^max; 1

А2 (р2 ) = {r(360° — р2) — r2 (р2 )} ^ may J.

где r1, r2 — уравнения окружностей левого и правого валков в полярной системе координат.

Проекцию А1 смещения А’ на направление угла а1 находим из треугольника ОА1В1 по теореме косинусов:

(R1 — А1)2 = r12 +(R1 + r0)2 -2r1(R1 + r1)cos(p1 — a1) , (6.9) откуда после преобразований

А1 = R1 — у/r12 + (R1 + r0)2 -2rj(R1 + r)cos(p1 — a). (6.10)

Аналогично находим проекцию Л2 смещения Л^ на направ­ление угла а2 из треугольника ОА2В2:

R2 ~л1 r22 + (R2 + r0)2 — 2r2 (R + r2)cos(p2 — a2). (6.11)

После базирования центр заготовки сместится в точку Оі и расстояние от него до центра левого валка будет равно А1О1 = = R1 + r0 + Ль а до центра правого валка А2О1 = R2 + r0 + Л2. Центр заготовки последовательно движется по левому валку по дуге окружности радиуса А1О1 и по правому валку по дуге ок­ружности радиуса А2О1. Пересечение этих траекторий и будет новым положением центра заготовки О1. Определим координа­ты точки О1 из совместного решения уравнений данных окруж­ностей в проекциях на оси X и Y:

-(R1 + r0) cos a1 + (R1 + r0 + Л1) cos ф1 = = (R2 + r0) cos a2 — (R2 + r0 + Л2) cos ф2;

-(R1 + r0) sin a1 + (R1 + r0 + Л1) sin ф1 =

= -(R2 + r0) sin a2 + (R2 + r0 +Л2) sin ф2,

где ф1 и ф2 — углы наклона отрезков А1О1 и А2О1 к оси X (см. рис. 6.5).

В уравнениях (6.12) первые слагаемые в левой и правой частях представляют собой проекции центров окружностей валков, а вто­рые слагаемые — проекции радиусов траекторий центра заготовки.

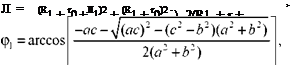Решение системы уравнений (6.12) дает выражения для рас­чета погрешности базирования:

где a = (R2 + r0)cos a2 + (R1 + r0)cos a1;

b = (R2 + r0)sina2 -(R1 + r0)sinaj;

c _ (R2 + ro + A2)2 — (q2 + b2) — (Ri + ro + Ai)2 2( Ri + ro + Ai)

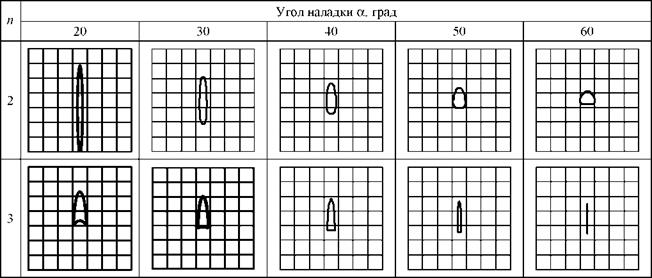
Исследуем траектории движения центра заготовки при ее вращении в зависимости от наладки бесцентрового суперфиниш­ного станка. В табл. 6.1 приведены расчетные траектории центра при одном обороте заготовки со средним радиусом r0 = 8 мм, имеющей отклонение формы в виде 2-, 3-, 4- и 5-й гармоник с ам­плитудами а2 = а3 = а4 = а5 = 1 мкм.

В качестве оптимизируемого параметра выступает суммар­ный угол a установки валков. Радиусы валков приняты R1 = R2 = = 62,5 мм и положение их центров А1 и А2 определено через па­раметры a1, a2 и r0. Так же, как и ранее, начальные фазы гармо­ник взяты равными нулю и углы установки валков относительно заготовки приняты равными a1 = a2.

Траектории движения центра при бесцентровом суперфи­нишировании похожи на траектории, полученные при бесцен­тровом шлифовании. Это объясняется тем, что радиусы валков многократно превышают отклонения формы заготовки и в окре­стности точек контакта мало отличаются от прямых.

Для 2-, 3-, 4- и 5-й гармоник рассчитан критерий K точности базирования в зависимости от наладочных углов валков. Результа­ты расчета представлены в табл. 6.2. Для 2-й гармоники при углах a = 10, 15° и для 3-й гармоники при угле a = 10° имеет место про­вал заготовки между валками в ряде положений при ее вращении. Поэтому критерий K для указанных случаев не вычислен.

Исследование критерия K показало, что для 2-, 3-, 4-, 5-й гар­моник оптимальным углом наладки в диапазоне a = 10… 60° явля­ется максимальное значение 60°. Для приведенных примеров при a = 10.60° значение критерия К изменяется от 1,0 до 4,5. По ана­логии с бесцентровым шлифованием с поперечной подачей можно предположить, что оптимальные углы наладки располагаются в пределах a = 80.110°, но реализация таких углов на суперфи­нишном станке невозможна по силовым ограничениям.

Траектории движения центра заготовки при бесцентровом суперфинишировании

п

Угол наладки а, град

20

30

40

50

60

4

I

А

А

*

А

Е

н

И

5

д

і

Л

1

|

А

Д

1

1

U

м

Таблица 6.2 Критерий K при бесцентровом суперфинишировании n Угол наладки а, град 10 15 20 25 30 35 40 45 50 55 60 2 — — 3,54 2,67 2,19 1,83 1,56 1,36 1,20 1,09 1,00 3 2,41 1,92 1,81 1,79 1,76 1,69 1,61 1,52 1,43 1,32 1,23 4 — 3,27 2,38 1,86 1,61 1,43 1,30 1,20 1,12 1,06 1,01 5 4,50 3,44 2,77 2,32 2,08 1,90 1,65 1,45 1,31 1,23 1,16

Для рассчитанного диапазона наладок критерий К принима­ет значения только больше единицы, что говорит о копировании погрешностей базовой поверхности и наличии тенденции к соз­данию новых погрешностей. При уменьшении отношения ра­диусов валков и заготовки наблюдается некоторое уменьшение критерия K. Однако, как будет показано далее, участие в про­цессе формообразования шлифовального бруска с большой площадью охвата поверхности заготовки создает условия для эффективного исправления погрешностей формы.

При оптимизации процесса бесцентрового суперфиниширо­вания по критерию точности базирования следует учитывать геометрические, кинематические и силовые ограничения. Гео­метрические ограничения накладываются исходя из расчета профиля валков на этапе профилирования или расчета формо­образующей траектории при наладке станка. Ограничения по силовым параметрам имеют нелинейный характер и выявляются при решении задачи силового замыкания контакта.

Помимо математической модели базирования, также разра­ботана модель формообразования поперечного сечения загото­вок при бесцентровом суперфинишировании. Предложенный подход основан на моделировании процесса съема припуска с учетом погрешностей базирования и изменения натягов в тех­нологической системе. В качестве обобщенного критерия фор­мообразования выступает коэффициент К1 исправления профи­ля, равный отношению исходного А отклонения от круглости к полученному после имитационной обработки Аі.

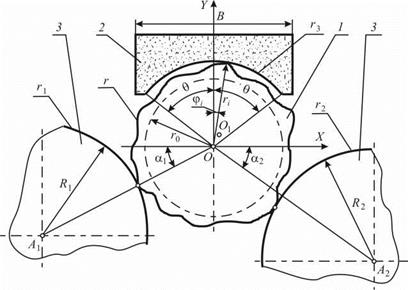
Расчетная схема формообразования представлена на рис. 6.6. Заготовка 1 базируется на двух валках 3. Брусок 2 в приработанном состоянии имеет образующую в виде дуги окружности радиуса r3 с углом охвата 20. Значение угла 0 зависит от соотношения ширины бруска, диаметра заготовки и величины приработки шлифовально­го бруска. Радиус r3 в процессе обработки меняется в пределах по­ловины поля допуска на диаметр заготовки. В рамках предложен­ной модели это не имеет принципиального значения, поэтому ра­диус образующей бруска принят постоянным.

Рис. 6.6. Схема формообразования при бесцентровом суперфинишировании

Поперечное сечение заготовки опишем следующим образом:

p

r = r0 +t + Xan cos(«9-9„^ (6.14)

n=2

где t — припуск на сторону.

В процессе обработки стабилизируются натяги в ТС, создан­ные исходными отклонениями формы заготовки и погрешностями базирования. При определении мгновенных натягов и мгновенных съемов металла приняты следующие допущения. Изменение ра­диуса заготовки по отношению к номинальному вызывает измене­ние натягов в ТС и, соответственно, давления шлифовального бру­ска. При постоянной жесткости резания приращение давления прямо пропорционально приращению снимаемого металла.

Радиальный съем металла 5 в пределах длины контакта за­готовки со шлифовальным бруском:

5 = r — r0 +tj — j + %Ar, (6.15)

где j — текущий оборот заготовки (1 < k < m); m — число оборотов заготовки, необходимое для съема припуска t; % — коэффициент, связанный с жесткостью резания.

При расчете величины 5 учитывают только положительные значения, при отрицательных значениях полагают 5 = 0. За j-й оборот заготовки в каждой точке профиля съем металла про­изойдет только один раз. Съем полного припуска t совершится за m оборотов заготовки.

При каждом текущем обороте заготовки 2jn получаем новый профиль rj, для которого заново рассчитываем погрешности бази­рования. После изменения угла ф до 2тп заготовку считают обра­ботанной. Окончательный съем металла произойдет на величину, большую, чем исходный припуск t. Это объясняется дополнитель­ным съемом металла из-за изменения натягов в ТС. Исходными данными при моделировании являются: радиус детали r0; парамет­ры профиля п; ап и фп; припуск t; максимальное число т оборотов заготовки при обработке; радиусы валков R1 и R2; ширина В шли­фовального бруска; углы а1 и а2 установки валков.

Получив дискретно заданный профиль детали после имита­ционной обработки, необходимо найти его аналитический экви­валент и определить отклонение от круглости. Если считать, что центры средней окружности детали до и после обработки совпа­дают с достаточной точностью, то параметры уравнения профи­ля в виде тригонометрического полинома (6.1) определяют по формулам Бесселя [61], а отклонение от круглости Д1 рассчиты­вают по стандартной методике [62]. В случае, когда полученное значение К1 меньше требуемого [K1], проводят параметриче­скую оптимизацию при наличии ограничений. Единообразное математическое представление профиля детали при формообра­зовании и измерении позволяет проанализировать не только комплексный показатель К1, но и изменение амплитудного со­става погрешностей.

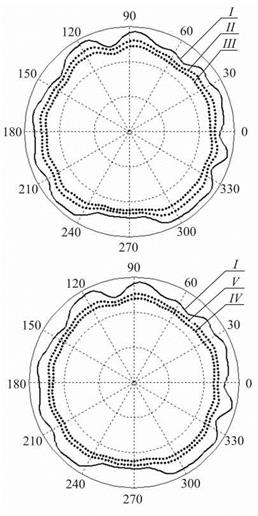
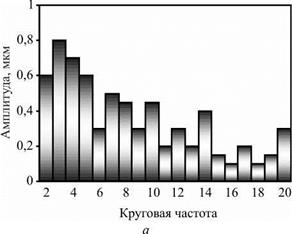
Рассмотрим пример моделирования процесса формообра­зования при следующих параметрах: r0 = 12 мм; t = 0,004 мм; m = 50; R1 = R2 = 60 мм; B = 12 мм; а1 є [35°; 15°]; а2 є [15°; 35 °]. Результаты представлены на рис. 6.7 в виде поперечных профилей детали: I — исходный; II — после обработки при ука­занных параметрах; III — после обработки с оптимальными уг­лами контакта (аі = 22°; а2 = 54°); IV — после обработки с уве­личенным припуском (t = 0,008 мм); V — после обработки с уве­личенной шириной бруска (B = 24 мм). Профили изображены в виде наложенных друг на друга круглограмм с совмещенными центрами, одинаковым радиальным масштабом увеличения и различными средними радиусами записи (для равномерного размещения профилей в зоне записи диаграммы). Амплитуды гармонических погрешностей детали для вариантов I-IV пред­ставлены на рис. 6.8.

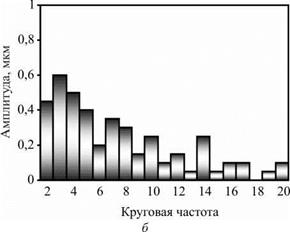
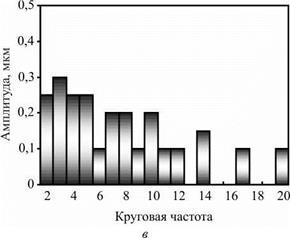
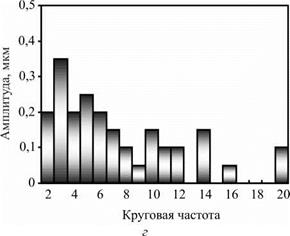
Исходное отклонение от круглости составило Д = 4,2 мкм. После имитационной обработки для вариантов II—V отклоне­ния от круглости Д1 равны 3,1; 2,2; 1,8; 1,7 мкм, коэффициент К1 исправления профиля равен 1,35; 1,91; 2,33; 2,47 соответ­ственно. Таким образом, увеличению критерия формообразо­вания К1 способствуют: увеличение ширины инструмента, припуска на обработку, а также оптимизация наладочных па­раметров станка.

Рис. 6.7. Расчетные круглограммы деталей

Анализ результатов моделирования показал, что наиболь­шее влияние на исправление профиля заготовки оказывают ши­рина шлифовального бруска и припуск на обработку. Однако наличие жестких технологических ограничений приводит к не­обходимости поиска других параметров оптимизации. Поэтому наиболее актуальными параметрами при оптимизации процесса формообразования следует считать углы контакта заготовки с валками. По итогам численных экспериментов рекомендована область оптимальных углов контакта, определяемая соотноше­ниями: а < а2 + 5°; а > 15°; аі + а2 < 90°, получившая приме­нение в разработке нового способа суперфиниширования [49].

Рис. 6.8. Амплитудный состав гармонических погрешностей профиля детали: а — вариант I; б — вариант II

Рис. 6.8. Окончание: в — вариант III; г — вариант IV

Наладка станков при обработке партии заготовок на основе статистического моделирования

Налаживать бесцентровые суперфинишные станки на обра­ботку одной конкретной заготовки нецелесообразно, а в партии отклонения формы заготовок имеют стохастический характер. Выявить одну доминирующую гармонику не всегда возможно, так как обычно имеются несколько гармоник со сравнительно большими амплитудами.

Для решения подобных задач используется метод статистиче­ского моделирования, также называемый методом статистических испытаний Монте-Карло [63]. Он базируется на применении слу­чайных чисел некоторой случайной величины с заданным распре­делением вероятности. Сущность метода статистического модели­рования сводится к построению моделирующего алгоритма, его реализации с помощью программно-технических средств ЭВМ и обработке данных методами математической статистики.

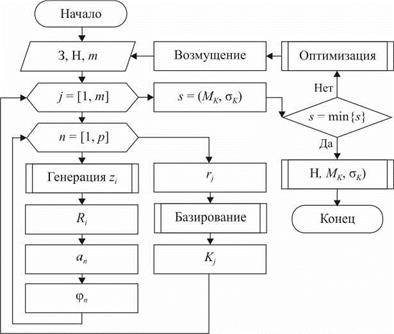
Применительно к наладке станков основная идея метода Мон­те-Карло заключается в моделировании стохастических входных данных (отклонений формы заготовок), многократной реализации аналитической модели базирования и получении вероятностных характеристик, численные значения которых совпадают с резуль­татом решения детерминированной задачи. В результате получают серию частных значений искомой погрешности базирования, ста­тистическая обработка которых дает сведения о влиянии парамет­ров наладки станка при обработке партии заготовок. Исходные данные о погрешностях формы заготовок получают эксперимен­тальным путем, а законы и параметры распределения рассчитыва­ют по формулам математической статистики. Если количество реализаций модели достаточно велико, то полученные результаты моделирования приобретают статистическую устойчивость и с достаточной точностью принимаются в виде оценок искомых па­раметров. Моделирующий алгоритм приведен на рис. 6.9.

Исходными данными при моделировании являются: пара­метры заготовки З (радиус r0, число n гармоник, параметры рас­пределения и границы интервала изменения амплитуд и началь­ных фаз гармоник), параметры наладки станка (углы базирую­щих элементов аь а2, радиусы валков Ль R2) и количество m за­готовок в партии. Число m заготовок в партии назначают, исхо­дя из трудоемкости моделирования, а не из реального техноло­гического процесса. Очевидно, что с увеличением числа реали­заций m возрастает точность и достоверность получаемых ста­тистических оценок.

Рис. 6.9. Моделирующий алгоритм наладки станка

Первый этап моделирования включает генерирование после­довательности случайных равномерно распределенных чисел z для каждой заготовки в партии в зависимости от числа гармоник про­филя. Полученные числа z преобразуют в требуемый закон рас­пределения для амплитуды at и начальной фазы фг — каждой гармо­ники. В результате формируют профиль одной заготовки rj.

На втором этапе рассчитывают погрешность базирования для каждой заготовки по аналитической модели и находят кри­терий точности базирования Kj.

На третьем этапе проводят статистическую обработку кри­терия K, вычисленного для всех заготовок в партии. В результа­те получают математическое ожидание Мк и среднеквадратиче­ское отклонение ок для критерия K. Далее проводят оптимиза­цию по указанным параметрам. Особенность заключается в том, что параметры Мк и ок имеют единый минимум.

Результаты статистического моделирования существенно за­висят от качества исходных последовательностей случайных чи­сел. На практике используют три основных способа генерации случайных чисел: аппаратный, табличный и алгоритмический. Ал­горитмический способ генерации случайных чисел наиболее ра­ционален при моделировании на компьютере. Его сущность состо­ит в том, что равномерно распределенная случайная величина в интервале [0, 1] имеет математическое ожидание m = ‘Л и диспер­сию а2 = 1/12. Получить непрерывное распределение на ЭВМ не-

2

П

у

случайных чисел того же интервала. Такой закон распределения называют квазиравномерным распределением. Случайная величи­на, имеющая квазиравномерное распределение в интервале [0, 1], принимает значения z = i/(2n — 1) с вероятностями pi = 1/2n, i = = 0, …, 2n — 1. В результате математическое ожидание квазиравно­мерной случайной величины совпадает с математическим ожида­нием равномерной случайной последовательности интервала [0, 1], а дисперсия отличается множителем (2n + 1)/(2n — 1), который при достаточно больших n близок к единице. Кроме того, для получе­ния значений z используют формулы (алгоритмы), поэтому такие детерминированные последовательности чисел называют псевдо­случайными.

В нашем случае требуется последовательность из примерно 2105 случайных чисел. Такой объем псевдослучайных чисел с определенным числом разрядов без повторений обеспечивает стандартный датчик случайных чисел random, имеющийся в большинстве языков и сред программирования. С целью улуч­шения качества последовательностей после генерирования пар­тии заготовок применяется метод возмущений, программно реа­лизованный в виде команды randomize. Эта функция позволяет избежать повторения результатов при многократных запусках программы.

Экспериментальные исследования установили, что между не­которыми амплитудами гармоник имеются значимые корреляци­онные связи. Для случайных погрешностей х и у с разными функ-

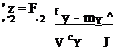циями распределения F(x), F2(y), математическими ожиданиями mx, my и среднеквадратическими отклонениями сх су целесообразно перейти к равномерно распределенным в интервале [0, 1] случай­ным величинам, воспользовавшись преобразованиями:

В этом случае коэффициент линейной корреляции находят по формуле [64]

При таком определении коэффициента корреляции упроща­ется решение задачи генерирования коррелированных случай­ных величин с разными законами распределения и исключается зависимость значения r от вида этих законов.

Воспользуемся последовательностью получения пары кор­релированных случайных чисел с разными законами распреде­ления, изложенной в работе [65]. На первом этапе генерируют три некоррелированных случайных числа А, В, С с равномерным распределением в интервале [0, 1]. Далее из них формируют па­ру коррелированных между собой чисел по формулам

у = ЛІГ* + BJ1-1 r*|;

11 V v (6.18) + 1-1 r* |.

Для выражений (6.18) можно строго доказать, что коэффи­циентом корреляции между случайными величинами yi и у2 яв­ляется r*, если значение г* определялось обычным образом. Числа у1 и у2 в общем случае распределены по симметричному трапецеидальному закону с большим s1 =^| r* | + ^/1-1 r* | и ма­

Далее выполняют преобразование трапецеидального рас­пределения чисел у1 и у2 в равномерное на интервале [0, 1] по следующим формулам:

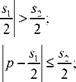— если у, > sx/2, то при р = s2 — yi

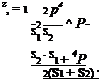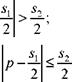— если у, < s1/2, то при р = у,

В результате получаем случайные числа z1 и z2, равномерно распределенные в интервале [0, 1] и имеющие, как показала со­ответствующая численная проверка, коэффициент корреляции |r|, связанный с |r*| соотношением

|r*| = |r| + 0,005086 + 0,01739sin(6,3986|r| + 5,9575). (6.21)

Таким образом, чтобы найти требуемое значение коэффи­циента корреляции r между случайными величинами z1 и z2, не­обходимо при формировании случайных чисел у1, у2 задать ве­личину |r*| по выражению (6.21). Абсолютная систематическая погрешность значения r при этом методе получения двух корре­лированных выборок не превышает 0,0025.

При перестановках в формулах (6.18) двух пар параметров А и В, А и С случайные величины z1 и z2 будут иметь коэффици­ент корреляции 1 — |r|, что позволит сформировать выборки двух случайных величин с коэффициентом корреляции ±(1 — |r|) и произвольными законами распределения.

Суммируемые случайные погрешности можно разделить на некоррелированные между собой группы трех типов: включаю­щие любое число некоррелированных погрешностей; жестко коррелированных между собой погрешностей с r = ±1 относи­тельно какой-либо одной погрешности из этой группы, приня­той за базовую; погрешностей с коэффициентом корреляции пар относительно одной базовой погрешности ±r и ±(1 — |r|). Групп второго и третьего типов может быть несколько, а значение r в каждой из них — произвольным. Если количество погрешностей в группе больше двух, то накладываются ограничения на пере­крестные коэффициенты корреляции. Например, нельзя одно­временно задать значения r12 = 1 и r13 = 1, если r23 Ф 1.

Для генерирования случайных чисел с заданным законом распределения используем метод инверсии, заключающийся в формировании последовательности случайных чисел z,, равно­мерно распределенных в интервале [0, 1], и последующем пре­образовании:

X=F -‘(z,-), (6.22)

где F-1(z,) — функция, обратная функции распределения случай­ной величины X,.

Количество случайных чисел, используемых для получения статистически устойчивой оценки параметров при реализации на ЭВМ, колеблется в широких пределах в зависимости от объ­екта моделирования, оцениваемых параметров, необходимой точности и достоверности результатов моделирования.

Приближенное число испытаний при моделировании мето­дом Монте-Карло определим по формуле

где ґдУ, n_i — коэффициент для вычисления двустороннего дове­рительного интервала математического ожидания; e — допусти­мая ошибка при оценке а.

Для определения допустимой погрешности e воспользуемся неравенством Чебышева, согласно которому для любого рас­пределения с конечным математическим ожиданием М и дис­персией а2 по крайней мере [1 — (1/k2)]100 % значений случай­ной величины находится в интервале М ± ka. Пределы по дан­ному выражению задаются с очень большим запасом. Считая, что не менее 99 % числа испытаний должны попасть в интервал М ± 3а, принимаем максимально допустимую ошибку e при оценке М в 0,2а. Максимальное среднеквадратическое отклоне­ние для амплитуд гармоник составляет 0,1 мкм, поэтому назна­чаем e = 0,02 мкм. При 99%-ном доверительном уровне и ориен­тировочном числе испытаний n = 200 получаем *ду, „_1 = 2,601. Число испытаний по формуле (6.23) равно n = 169. Принимаем число заготовок в партии при моделировании m = 200. Тогда с 99%-ной вероятностью не менее 99 % от числа испытаний при моделировании попадет в интервал (0,1 ± 0,06) мкм.

Экспериментальные исследования выявили, что амплитуды а гармоник распределены по закону Пирсона первого типа (бе­та-распределение), а начальные фазы ф — по закону равной веро­ятности.

Функция плотности вероятности ^-распределения амплитуд гармоник имеет вид

где Г — гамма-функция; n, М — параметры ^-распределения; х — случайная величина.

Гамма-функция имеет вид

Г(у) = JхY-1e-xdx. (6.25)

0

Функция распределения начальных фаз гармоник имеет вид

F (х) = (х — а) / (b — а), (6.26)

где а, b — границы интервала изменения начальной фазы ф.

Поскольку a = 0°, b = 360°, имеем следующее выражение для функции распределения начальных фаз:

F(x) = x /360. (6.27)

В общем случае, зная плотность вероятности f х), необхо­димо выбрать случайное число z, и решить относительно х, ин­тегральное уравнение:

x

j f(xi) dxi = zi,

a

где a — наименьшее значение x,.

Для равномерного распределения обратная функция имеет явный вид, и преобразование случайной величины z, в случай­ную величину xi осуществляют по выражению

x = 360z,. (6.29)

Методика получения случайных величин, имеющих различ­ные законы распределения, с помощью нормированных случай­ных величин изложена в работах [64, 67].

Параметры ^-распределения п и ц, полученные в результате статистической обработки экспериментальных данных, имеют нецелые значения. Поэтому применим следующий метод гене­рации. Вычислим

S = z11/п, S2 = zf, (6.30)

где z1, z2 — независимые друг от друга равномерно распределен­ные случайные числа.

Если S1 + S2 > 1, то возьмем еще одну пару случайных чисел z1, z2 и проделаем те же операции. Если S1 + S2 < 1, то

Полученные по формулам (6.25)-(6.31) распределения яв­ляются нормированными, т. е. находятся в интервале [0, 1]. По-

лучить распределения в интервале [аь а2] можно с помощью по­следующего преобразования:

На основе разработанного алгоритма (рис. 6.9), формул (6.16)-(6.32) и экспериментальных данных проведено модели­рование критерия точности базирования для партии из 200 заго­товок для бесцентрового суперфиниширования [66]. Статисти­ческая обработка результатов показала, что наилучшим образом критерий K описывается нормальным законом при суперфини­шировании. Функция плотности вероятности в этом случае од­нозначно определена двумя параметрами — математическим ожиданием m и среднеквадратическим отклонением а.

По результатам статистического моделирования рассчитаны первые четыре статистические момента (m1, m2, m3, m4), средне­квадратическое отклонение а, показатели асимметрии а3 и экс­цесса а4 для распределения критерия K, которые приведены в табл. 6.3. Параметр наладки станка а имеет тот же смысл, что и ранее.

Таблица 6.3 Начальные моменты распределения критерия K в партии заготовок а m1 m2 а m^ а3 m4 а4 15 1,400 0,123 0,351 0,012 0,277 0,043 2,858 30 0,809 0,049 0,221 0,004 0,007 0,393 2,790 45 0,603 0,020 0,141 0,001 0,001 0,306 3,154

Анализ табл. 6.3 показал, что все варианты характеризуются положительным показателем асимметрии и показателем эксцесса, равным 3 и более. При суперфинишировании наиболее нерацио­нальный угол а = 15° (МО погрешности базирования равно 1,4 мкм и СКО равно 0,351 мкм). При наилучшем угле наладки а = 45° МО уменьшается примерно в 2,3 раза и СКО — в 2,5 раза. Столь большие различия статистических оценок критерия K по
сравнению со шлифованием объясняются тем, что оптимальный вариант наладки находится вне исследуемого диапазона угла а = 15.. .45°. При наличии ограничений на максимальное значение угла а уменьшение МО и СКО составит примерно 50 %.

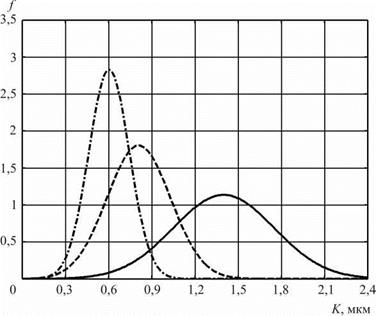
Графики плотности вероятности f соответственно для трех рассчитанных вариантов наладки изображены на рис. 6.10.

Рис. 6.10. Плотность вероятности критерия K в зависимости от наладки станка: сплошная линия — а = 15°; штриховая — а = 30°; штрихпунктирная — а = 45°

Сравнение оценок математического ожидания для критерия базирования с величиной отклонения от круглости показало, что оптимальные варианты наладки шлифовального и суперфиниш­ного станков способствуют активному исправлению профиля поперечного сечения. Кроме того, наименьшему математиче­скому ожиданию также соответствует наименьшее среднеквад­ратическое отклонение (имеют единый минимум).

Для оценок математического ожидания и среднеквадратиче­ского отклонения целесообразно вычислить доверительные ин­тервалы. В случае нормально или асимптотически нормально распределенных величин при больших выборках и неизвестных параметрах распределения (определяемых по эмпирическим данным) используют, согласно работе [68], следующие форму­лы. Доверительный интервал для математического ожидания т, отвечающий доверительной вероятности р = 1 — q/100:

а а

т — tq~i=7, т + tM==T Vn -1 ып -1

где tq — критерий Стьюдента (прир = 0,95 имеем tq = 1,960).

Доверительный интервал для математического ожидания т, отвечающий доверительной вероятности р = 1 — q/100 при нор­мальном распределении:

при асимптотически нормальном распределении

Результаты расчета доверительных интервалов по форму­лам (6.33)-(6.35) для данных из табл. 6.3 приведены в табл. 6.4.

Доверительные интервалы для распределения
критерия K в партии заготовок

Таблица 6.4 а Интервал для т, мкм Интервал для а, мкм 15 0,098 0,017 30 0,062 0,011 45 0,040 0,007

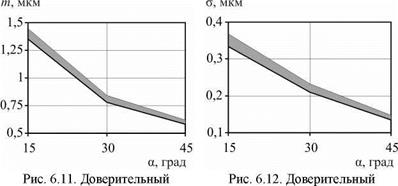
Графическая интерпретация доверительных интервалов ре­зультатов моделирования при бесцентровом суперфиниширова­нии представлена на рис. 6.11 — для математического ожидания, на рис. 6.12 — для среднеквадратического отклонения.

интервал для математического интервал для среднеквадрати-

ожидания ческого отклонения

Анализ табл. 6.4 показал, что с уменьшением точечных оце­нок математического ожидания и среднеквадратического откло­нения уменьшается и величина доверительных интервалов для этих параметров.