ФОРМООБРАЗОВАНИЕ ПОПЕРЕЧНОГО СЕЧЕНИЯ ЗАГОТОВОК ПРИ СУПЕРФИНИШИРОВАНИИ

6.1. Общий подход к обеспечению точности формы
в поперечном сечении заготовок

Бесцентровой абразивной обработке присущи сложные фи­зико-механические и геометро-кинематические закономерности формообразования. В общем случае при обеспечении точности следует учитывать большое число различных по математиче­скому и физическому описанию факторов. Многие из этих фак­торов неуправляемы при обработке, другие же сложно формали­зовать или требуются экспериментальные исследования. Анализ некоторых физических факторов требует дополнительного ус­тановления их функциональной связи с параметрами качества обрабатываемых деталей. Указанные сложности привели к тому, что реализация системного подхода представляет собой трудно разрешимую задачу. Поэтому в настоящее время известны мно­гочисленные частные математические и физические модели, как правило, с одним критерием оптимальности и ограниченным числом учитываемых параметров.

Точность формы поверхностей вращения зависит от точно­сти двух основных элементов — образующей и направляющей. Образующая в общем случае может иметь произвольную форму, но на практике чаще всего представляет собой прямую (цилинд­рические и конические поверхности) или окружность (сфериче­ские и тороидальные поверхности). Для нормирования точности формы в продольном сечении используют комплексный показа­тель — отклонение профиля продольного сечения.

Идеальная форма поперечного сечения тела вращения пред­ставляет собой круг. Точность формы в поперечном сечении нормируют с помощью комплексного показателя — отклонения от круглости, а также частных видов отклонений — овальности и огранки.

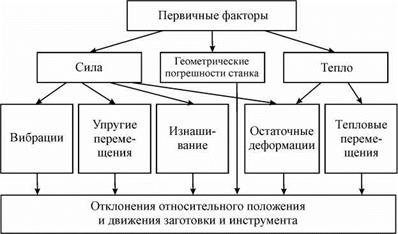
Любое технологическое воздействие имеет соответствую­щую физическую природу, определяющую характер взаимодей­ствия элементов технологической системы. Многочисленные исследования точности машин [1, 3, 4, 11, 16 и др.] показали, что большинство факторов влияют на погрешности через силу и тепло. Последние, в свою очередь, вызывают различного рода перемещения элементов ТС и тем самым нарушают заданное относительное положение или движение элементов ТС. Первич­ные факторы через силу и тепло воздействуют на заготовки, вы­зывая их тепловые и упругие перемещения, изнашивание, оста­точные деформации и вибрации (рис. 6.1). К первичным факто­рам также можно отнести геометрические погрешности элемен­тов станка, которые непосредственно влияют на нарушение от­носительного движения инструмента и заготовки.

Рис. 6.1. Влияние первичных факторов на точность обработки

Наиболее известен расчетно-аналитический метод опреде­ления суммарной погрешности механической обработки, соз­данный научными школами А. П. Соколовского и В. М. Кована, который опирается на принцип суперпозиции. Действие каждой из составляющих погрешности рассматривается независимо от других, а суммарная погрешность складывается суммированием элементарных по определенным правилам. Метод оправдывает себя в очень жестко регламентированных условиях, когда пара­метры технологических процессов не изменяются или изменя­ются незначительно. В общем случае суммарная погрешность формируется из первичных погрешностей, общее число которых превышает 20.

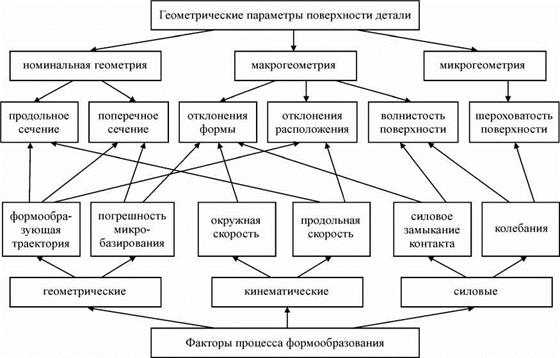
Функциональные связи геометрических, кинематических и силовых параметров формообразования и геометрии деталей при бесцентровой абразивной обработке показаны на рис. 6.2.

Экспериментальными исследованиями установлена значи­тельная склонность бесцентрового шлифования и суперфини­ширования к технологическому наследованию погрешностей формы поверхностей заготовок. Технологическим наследовани­ем называют явление переноса свойств объектов от предшест­вующих технологических операций к последующим. Научный анализ вопросов технологического наследования пока не нашел в технической литературе [1, 3, 4] достаточно полного отраже­ния. Представление процесса наследования обычно восприни­мается как процесс детерминированный. Это означает, что при одном и том же комплексе исходных параметров при каждом последующем повторении операций будет возникать один и тот же результат. Вместе с тем становится очевидным, что детерми­нированный подход к явлению несколько обедняет его пред­ставление. Более полным должен быть учет случайного фактора. Действительно, любой технологический процесс характеризует­ся целым рядом параметров, которые имеют случайный харак­тер. Все эти параметры случайным образом суммируются в ходе технологического процесса, поэтому и результат представляется случайной величиной.

Основными моментами технологической наследственности являются установление факта переноса определенного свойства от предшествующей операции к последующим, а также количе­ственная сторона вопроса. Объективное существование наслед­ственных связей не означает, что во всех случаях их необходимо

Рис. 6.2. Функциональные связи параметров формообразования и геометрии деталей при бесцентровом суперфинишировании

учитывать. Если, например, речь идет об изготовлении машино­строительных изделий нормальной точности, наследственная до­ля погрешности может оказаться сравнительно малой. Основны­ми будут традиционные погрешности, характерные для большин­ства технологических процессов изготовления машин. В тех же случаях, когда допустимые погрешности должны быть малыми по величине и их устранение представляется достаточно сложной технологической задачей, наследственная доля допуска может не только быть соизмеримой с допуском, но и превосходить его. Следовательно, закономерности технологического наследования необходимо использовать прежде всего в прецизионном машино­строении.

Анализ литературных данных, экспериментальные исследо­вания и многолетний опыт эксплуатации станков в подшипни­ковой промышленности показали, что вклад геометрических, кинематических и силовых факторов при бесцентровом шлифо­вании составляет примерно 50 %.

Предлагаемая методология исследований рассматривает процесс формообразования с декомпозицией на подсистемы и описание их детерминированными и стохастическими моделя­ми. Основной является формообразующая подсистема, заданная детерминированными геометрическими, кинематическими и си­ловыми параметрами. Именно в этой подсистеме формируются показатели технологической надежности. Влияние других под­систем рассматривается в виде возмущающих воздействий. В большинстве случаев они имеют стохастическую природу.

Для анализа процесса формообразования создана система критериальных оценок точности обработки через параметры на­ладки оборудования, включающая: результирующий вектор от­клонений формообразующей траектории; приведенную погреш­ность базирования; статистические коэффициенты исправления формы заготовок. Результирующий вектор отклонений траекто­рии заготовок относительно инструмента определяется по детер­минированным геометрическим моделям с учетом погрешностей элементов формообразующей подсистемы станка и точности ус­тановки наладочных параметров. Приведенная погрешность ба­зирования представляет собой безразмерный коэффициент, пока­зывающий отношение среднеарифметического значения (САЗ) мгновенных погрешностей базирования при перемещении заго­товки к отклонению формы заготовки, вызывающей эту погреш­ность. Статистические коэффициенты исправления формы заго­товок (как правило, среднеарифметическое значение и средне­квадратическое отклонение (СКО)) формируются на основании экспериментальных данных или в результате моделирования по методу Монте-Карло с учетом стохастической природы этих дан­ных. При минимизации целевой функции основной критерий вы­бирается по максиминному принципу, а остальные критерии ста­новятся ограничениями задачи.

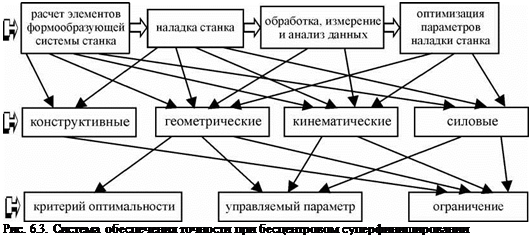
Задача обеспечения точности решается на этапах проекти­рования, наладки станков, обработки, измерения и подналадки станков на основе оптимизации (рис. 6.3). На этапе проектиро­вания выполняют расчет формообразующих элементов: профи­лирование ведущего круга бесцентровых шлифовальных стан­ков и валков суперфинишных станков, расчет параметров уст­ройства правки абразивных кругов, формообразование валков суперфинишного станка.

На этапе наладки в первую очередь определяют кинематиче­ские и силовые параметры процесса, их изменение в зависимости от геометрической наладки станка. Устанавливают влияние точ­ности наладочных параметров на погрешности относительной траектории заготовки и инструмента. При суперфинишировании различных деталей на валках постоянного профиля рассчитывают параметры формообразующей траектории.

Измерительная задача при исследовании процессов образо­вания погрешностей в условиях технологического наследования состоит в том, чтобы построить измерение не величины, а про­цесса и оценить возможные погрешности измерения процесса. Методологическая основа такого подхода к решению задачи из­мерения состоит в том, что процесс, с точки зрения классифика­ции причин появления погрешностей, можно представить как

траекторию относительного движения, отображенную в обраба­тываемой реальной поверхности, которую, в свою очередь, можно разделить на номинальную (заданную в технологических документах) и возмущенную (определяющую появление по­грешностей поверхности).

При измерении наследуемых геометрических отклонений воз­никают две проблемы: минимизация методической составляющей погрешности измерения и получение в процессе измерения ин­формации о наследуемой составляющей погрешности. Решение этих проблем связано как с разработкой методов и средств измере­ний, так и с выбором эффективных методов обработки измери­тельной информации. Особенность измерения в процессе обработ­ки состоит в том, что, стремясь уменьшить погрешность измерения за счет сокращения метрологической размерной цепи, за измери­тельную базу принимают обрабатываемую поверхность. Послед­нее приводит к двух — или трехточечным схемам измерения, где из­меряется величина, отличная от радиуса поверхности.

В процессе обработки рассматривают формообразование отклонений формы поверхностей из-за погрешностей базирова­ния, зависящих как от параметров наладки станков, так и от ис­ходной геометрии заготовок [51]. Выявление этих погрешностей на этапе измерения позволяет оптимизировать процесс обработ­ки введением подналадки. Как правило, величина подналадки мала по сравнению с основной наладкой, но в ряде случаев не­обходим проверочный расчет кинематических и силовых пара­метров. Для нахождения оптимальных наладочных параметров требуется применение формальных методов оптимизации.

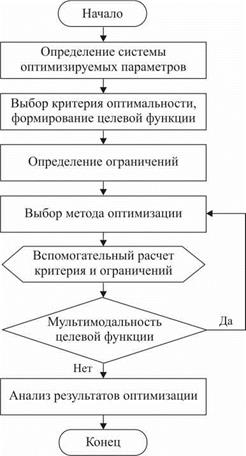
Постановка и решение задачи оптимизации геометро­кинематических параметров процесса бесцентровой абразивной обработки (рис. 6.4) включают следующие основные подэтапы:

• выделение системы оптимизируемых параметров;

• формулировка критерия оптимизации, определение це­левой функции;

• определение системы ограничений;

• выбор конкретного метода оптимизации.

Рис. 6.4. Структурная схема оптимизации

На первом подэтапе определяют систему оптимизируемых па­раметров, которыми возможно управлять при наладке станка и от которых зависят критерии точности обработки. Среди данных па­раметров выделяют внешние — формирующие окончательную це­левую функцию, и внутренние — используемые для вспомогатель­ных расчетов критериев и ограничений. Внешними параметрами являются углы контакта заготовки с базирующими элементами станка и параметры наладки бесцентрового суперфинишного стан­ка (угол перекрещивания и межосевое расстояние валков). К внут­ренним параметрам относят переменные, подлежащие определе­нию в геометрической, кинематической и силовой задачах при численном методе их решения. Необходимость во внутренних па­раметрах возникает, когда целевая функция рассчитывается по ал­горитму, а внешние параметры определяются через внутренние.

Учтены ограничения трех типов: параметрические, функцио­нальные и критериальные. Параметрические ограничения в данном случае имеют вид неравенств для отдельных параметров. К ним относят в первую очередь конструктивные ограничения при налад­ке станков с продольной подачей. Функциональные ограничения выражаются в виде равенств или неравенств функций от различ­ных параметров. Такими ограничениями служат решения кинема­тической и силовой задач. Критериальное ограничение имеет ме­сто, когда один из критериев выступает как ограничение. Тогда на­кладывается ограничение на предельные значения данного выход­ного параметра, исходя из технических требований к детали.

Целевая функция формируется по максиминному критерию, т. е. наиболее неблагополучному с позиций выполнения условий работоспособности выходного параметра. В общем виде целевая функция F(X) определяется по выражению

F(X) = max min У (X), (6.1)

XeDxje[1:m] 1

где Х — вектор оптимизируемых параметров; Dx — область рабо­тоспособности; m — число выходных параметров (критериев).

Запас работоспособности У для 7-го выходного параметра:

Sj = (Tj — yj)/Tj (6.2)

или

S = (Т; — yjj, (6.3)

где yj — выходной параметр; Tj — техническое требование для 7-го выходного параметра; уном/ — номинальное значение; 5;- — харак­теристика рассеяния j-го выходного параметра (например, трех — сигмовый допуск).

Безусловная целевая функция F(X) определена выражением (6.1) и с учетом ограничений преобразовывается в функцию Q(X) на основе метода штрафных функций:

Q(X) = F(X) + U(X), (6.4)

где U(X) — функция штрафа.

Функция штрафа U(X) учитывает нарушение ограничений типа равенств фі (X) = 0 и неравенств ф, (X) > 0 и имеет вид

n m

U(X) = гX (Фг (X))2 + ГXminty, (X)}2, (6.5)

і=і j=i

где n, m — число ограничений типа равенств и неравенств соот­ветственно; г1, г2 — коэффициенты, подбираемые исходя из тре­бований точности и экономичности вычислений.

При наладке технологического оборудования на обработку партий заготовок возникает необходимость в учете стохастиче­ского характера некоторых параметров моделей. Для решения подобных задач предназначен метод статистического моделиро­вания, также называемый методом статистических испытаний Монте-Карло [52]. Он базируется на применении случайных чи­сел некоторой случайной величины с заданным распределением вероятности. Сущность метода статистического моделирования сводится к построению моделирующего алгоритма, его реализа­ции с помощью программно-технических средств ЭВМ и обра­ботке данных методами математической статистики.

Применительно к задаче наладки технологического обору­дования основная идея метода Монте-Карло заключается в мо­делировании стохастических входных данных, многократной реализации аналитической модели базирования и получении ве­роятностных характеристик, численные значения которых сов­падают с результатом решения детерминированной задачи. В результате получают серию частных значений искомой по­грешности базирования, статистическая обработка которых дает сведения о влиянии параметров наладки станка на точность об­работки партии заготовок. Исходные данные о погрешностях формы заготовок получают экспериментальным путем, а законы и параметры распределения рассчитывают по формулам мате­матической статистики. Если количество реализаций достаточно велико, то полученные результаты моделирования приобретают статистическую устойчивость и с достаточной точностью при­нимаются в виде оценок искомых параметров.

Таким образом, предложенная методология обеспечения точности бесцентровой абразивной обработки основана на оп­тимизации геометро-кинематических параметров формообразо­вания на этапах проектирования и эксплуатации оборудования с учетом детерминированных и стохастических факторов и тех­нологической наследственности.

Отклонения формы принято описывать тригонометриче­ским полиномом, так как большинство факторов процесса фор­мообразования имеют периодический характер [54]. Таким об­разом, поперечное сечение заготовки в полярной системе коор­динат задается тригонометрическим полиномом вида

p

r = r + Xan cos(«9-9„), (6.6)

n=2

где r0 — радиус средней окружности профиля заготовки; n — кру­говая частота (текущий номер гармоники); ап — амплитуда n-й гармоники; ф — полярный угол; фп — начальная фаза n-й гармо­ники; р — максимальное число гармоник.

Описание поперечного профиля заготовки формулой (6.6) подразумевает, что в качестве базовой окружности выступает средняя окружность, полученная методом наименьших квадра­тов. Первая гармоника не рассматривается, так как она в первом приближении представляет собой эксцентриситет центров сред­ней окружности и начала системы координат [55].

Для бесцентрового суперфиниширования характерна склон­ность к геометрическому наследованию погрешностей формы. Причем в процесс формообразования существенный вклад вносит погрешность базирования, когда копируются исходные погреш­ности формы заготовки и формируются новые, обусловленные собственно погрешностями базирования. Многочисленные ис­следования доказали, что процесс бесцентрового базирования управляем за счет наладки станков. Теоретические основы для указанных технологических операций заложены в 60-70-х гг. ХХ в. и отражены как в конструктивных особенностях станков, так и в методиках их наладки. Однако многолетний опыт экс­плуатации подобного оборудования показал, что во многих слу­чаях требуемая точность формы заготовок в поперечном сечении не обеспечивается.

Анализ существующих математических моделей базирова­ния при бесцентровом суперфинишировании [56-59] установил, что погрешность расчета по ним составляет в среднем 50-100 %. Такая существенная погрешность вызвана значительными уп­рощениями и допущениями при формализации задачи. В каче­стве критериев в известных работах предложены отношения возникающих при обработке натягов в технологической системе или амплитуд гармоник обрабатываемой поверхности к величи­не исходной погрешности базовой поверхности заготовки.

Общий недостаток указанных работ — отсутствие визуализа­ции при вращении заготовки, что не позволило оценить погрешно­сти решения. Другой недостаток, присущий почти всем исследова­ниям, заключается в раздельном рассмотрении гармоник. Сумми­рование результатов для отдельных гармоник дает некорректные результаты, так как принцип суперпозиций не выполняется даже при нулевых начальных фазах гармоник. Кроме того, предложен­ные критерии, описывающие процесс базирования или формообра­зования, не всегда имеют однозначную математическую трактовку и, как следствие, не позволяют эффективно управлять процессом. Приведенные факты указывают на необходимость пересмотра тео­ретических аспектов формообразования поперечного сечения де­талей при бесцентровой абразивной обработке.

При анализе формообразования поперечного сечения не­обходимо вначале рассчитать погрешность базирования. По определению, погрешность базирования — отклонение факти­чески достигнутого положения заготовки от требуемого. Под требуемым положением следует понимать положение геомет­рически точной цилиндрической заготовки, заданное наладоч­ными параметрами станка, относительно которого устанавли­вают инструмент.

ГОСТ 21495-76 содержит 24 стандартизованных термина и их определения, однако с их помощью не удается корректно описать процесс бесцентрового базирования. В работе [60] от­мечено, что часть из них следует исключить как несоответст­вующие сути вопроса и в то же время ввести ряд новых терми­нов, а для некоторых известных терминов следует дать иные оп­ределения. При базировании заготовок нужно использовать од­ну или несколько взаимосвязанных декартовых или полярных систем координат (последние целесообразны для тел вращения). Системы координат подразделяют по назначению — на основные и дополнительные, по стабильности положения в пространстве — на неподвижные и подвижные. Основная система используется для отсчета заданного при базировании заготовки номинального положения или размера и для координирования дополнительных систем. Дополнительная система определяет достигнутое при базировании заготовки положение в основной системе коорди­нат. Подвижная система координат необходима в случае, когда при базировании у заготовки отнимают не все степени свободы.

Бесцентровая обработка имеет особенность — заготовка со­храняет несколько степеней свободы — прямолинейные переме­щения в плоскости, перпендикулярной ее оси и возможность поворота при обработке с продольной подачей. Тогда основная неподвижная декартовая система координат имеет начало в цен­тре профиля заготовки, находящейся в номинальном положе­нии. Дополнительную подвижную полярную систему координат необходимо связать с центром профиля заготовки в процессе ее вращения (и перемещения). Таким образом, положение допол­нительной подвижной системы координат в основной непод­вижной декартовой системе координат и определит искомую погрешность базирования.

При бесцентровой обработке заготовка непрерывно враща­ется и центр ее сечения постоянно смещается. Поэтому погреш­ность базирования А представляет собой переменную величину. После одного оборота центр профиля заготовки опишет некото­рый замкнутый контур, который и характеризует погрешность базирования.

Предлагается критерий точности бесцентрового базирова­ния в виде среднего арифметического радиусов, определяющих центр профиля в основной системе координат, при одном обо­роте заготовки:

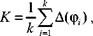(6.7)

где фг- — угол поворота заготовки; k — число расчетных точек тра­ектории.

Критерий K имеет однозначное математическое описание, измеряется в миллиметрах. Он всегда представляет собой поло­жительное число, так как величина А есть модуль радиус­вектора. Деление на число точек k введено для нормирования критерия K. Также предложенный критерий не зависит от ис­ходного выбора начала дополнительной подвижной системы координат.