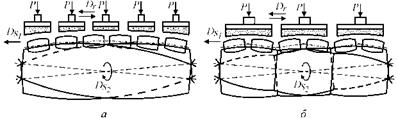
При суперфинишировании бомбинированных поверхностей в зависимости от их размеров и применяемого оборудования возможны две схемы обработки: с движением заготовки по дуге окружности под всеми суперфинишными станциями (рис. 5.8, а) и с движением заготовки по дуге окружности под каждой из суперфинишных станций (рис. 5.8, б). Соответственно применяют два варианта валков: одно — и многоволновые (как правило, по числу суперфинишных станций станка). Также в зависимости от диаметра и величины радиуса бомбины заготовка исходно может быть цилиндрической или бомбинированной с радиусом, близким к радиусу бомбины детали.
Исходная посылка состоит в том, что образующая заготовки однозначно определена траекторией ее движения на валковом устройстве [47, 48]. Профиль осевого сечения валков должен задавать дуговую формообразующую траекторию относительно направления осцилляции брусков.
|
Рис. 5.8. Схемы бесцентрового суперфиниширования бомбинированных поверхностей |
Для создания бомбинированной поверхности на детали траектория ее движения представляет собой дугу окружности радиуса R, согласованного по величине с радиусом бомбины R1. В первом приближении можно считать радиусы равными R = R1. Необходимо отметить, что в данной схеме формообразования заготовка имеет точечный контакт с валками. При этом для принятия устойчивого положения в процессе движения заготовка может дополнительно поворачиваться в вертикальной плоскости. Это следует учитывать при назначении R < R1. Более точные данные по выбору радиуса R получают на основе экспериментальных данных. Формально данное условие выполняется, если ось заготовки в любой момент является касательной к окружности радиуса R, определенной в системе суперфинишного станка требуемыми наладочными координатами. Полагаем, что скорость вращения валков многократно превышает скорость продольной подачи заготовки.
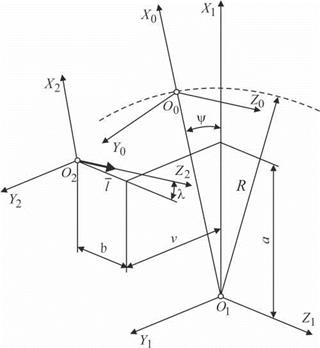
Введем в рассмотрение следующие координатные системы (рис. 5.9): S0(X0 О0 Y0 Z0) — система заготовки; S1(X1 О1 Y Z1) — условно неподвижная вспомогательная система; S2(X2 О2 Y2 Z2) — система валка. Система координат Si по отношению к системе S0
|
Рис. 5.9. Координатная схема профилирования валков для обработки бомбинированных поверхностей |
повернута вокруг оси Y против часовой стрелки на угол у и смещена в этом же направлении на величину — R. Система координат S2 по отношению к системе Si повернута вокруг оси Y против часовой стрелки на угол X и смещена по оси X на величину а, по оси Y — на величину v и по оси Z — на величину — b.
Наладочная координата а совместно с координатой v определяет максимальный расчетный радиус валка. Координата b предназначена для расчета многоволновых валков и задает положение текущей волны относительно плоскости Z1 = 0.
Для преобразования координат поверхности детали из системы S0 в систему S2 воспользуемся матричным равенством:
Г1 = M21M10 ‘ ro, (531)
 |
 |
 |
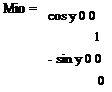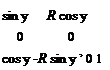где М21 — матрица перехода из системы координат S1 в систему S2; М10 — матрица перехода из системы координат S0 в систему Si. Матрица перехода М10 имеет вид
где у — независимый угловой параметр; R — радиус траектории движения заготовок.
Матрица перехода М21 имеет вид
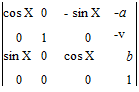(5.33)
где 2X — угол перекрещивания осей валков; 2v — межосевое расстояние валков; а — вертикальная наладочная координата станка; b — координата, задающая положение текущей волны для многоволновых валков.
Поверхность цилиндрической заготовки (рис. 5.10, а) в векторно-параметрической форме в системе S0 опишем уравнением
r0 = — r sin ф-i + r cos Ф ■ j + lt ■ к, (5.34)
где r — радиус заготовки; ф, к — криволинейные координаты цилиндрической поверхности.
Поверхность бомбинированной заготовки (рис. 5.10, б) в векторно-параметрической форме в системе S0 опишем уравнением
r0 = — ri sinф■ i + ri cosФ ■ j + lt ■ к, (5.35)
где r — текущий радиус заготовки, rt = ^R2 -1f -^Jr? -12 + r1;
r1 — максимальный радиус бомбинированной заготовки; R1 — радиус бомбины.
В проекциях уравнения, описывающие семейство поверхностей валка для исходно цилиндрической заготовки:
 |
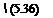
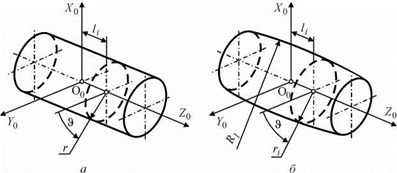X2 = — rsinOcos(y-X) + lj sin(y-X) + Rcos(y-X)-a; Y2 = r cos O — v;
Z2 = r sin Osin(y — X) + lt cos(y — X) — R sin(y — X) + b.
 |
 |
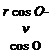
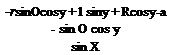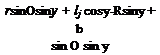Для определения искомой поверхности валка необходимо найти контактную линию из условия пересечения нормали к поверхности заготовки с осью валка. Данное условие в системе координат S1 имеет вид
(5.37)
 |
 |
Из выражения (5.37) установим связь между криволинейными координатами O и l{.
Уравнение (5.38) так же, как и в случае профилирования валков для обработки цилиндрических деталей, имеет два реше-
ния Ф1 и Ф2. Выбор правильного корня очевиден и задан началом отсчета угла Ф (см. рис. 5.9).
Окончательно поверхность валка опишется уравнениями:
X2 = — rsin$cos(y — X) + lt sin(y — X) + Rcos(y — X) — a; Y2 = r cos Ф — v;
Z2 =r sin$sin(y — X) + lt cos(y — X) — Rsin(y — X) + b; t ф= lt sin(y-X) + Rcos(y-X) — acosX-bsinX v cos(y-X)
Аналогично можно получить уравнения, описывающие поверхность валка, образованную исходно бомбинированной заготовкой. Эти уравнения не приведены, так как исследования показали, что при радиусе бомбины R = 500.. .3000 мм получаемые результаты мало отличаются от данных для цилиндрической заготовки.
При произвольном выборе параметров наладки станка возможен случай, когда ось заготовки будет находиться ниже осей валков. При этом формальное решение по изложенной методике также имеет место, однако оно противоречит геометрическому смыслу задачи. Условие расположения оси заготовки выше осей валков приближенно выражают следующим неравенством:
a < 0,5Lctgn — 0,5L sin X — r secn, (5.40)
где n = arcsin(0,5L/R); L — длина валка.
Профиль валка как тела вращения целесообразно задавать
координатами (Z2, R2), где R2 =*JX2 + Y22 . Однако в этом случае
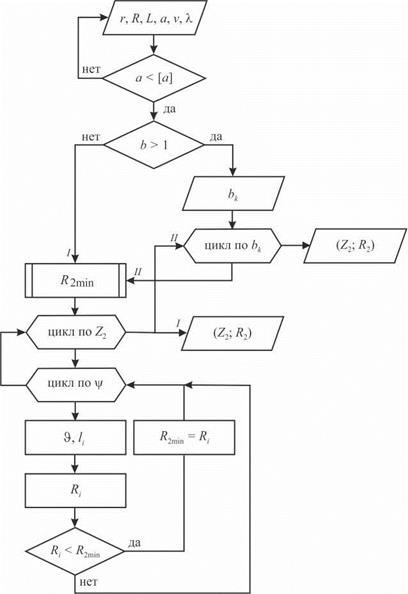
число неизвестных параметров превышает число составленных уравнений, поэтому требуется численный метод решения. Алгоритм численного профилирования валков дан на рис. 5.11. Последовательность расчета профиля валка:
• вводят исходные данные заготовки и параметров наладки станка;
• проверяют параметры наладки станка на выполнение условия расположения заготовки выше осей валков — формула (5.40);
|
Рис. 5.11. Алгоритм профилирования валков бесцентрового суперфинишного станка для обработки бомбинированных поверхностей |
• задают тип валка (одно-, многоволновый);
• для многоволнового валка подсчитывают координаты bk (к — число волн) и организуют цикл по bk;
• организуют цикл по осевому сечению Z2;
• организуют цикл по угловому параметру у;
• решают систему из двух последних уравнений (5.39) относительно неизвестных криволинейных координат Ф и lі;
• рассчитывают радиусы валка R;
• находят минимальный радиус валка в данном сечении R2mn,
• выводят данные (Z2, R2).
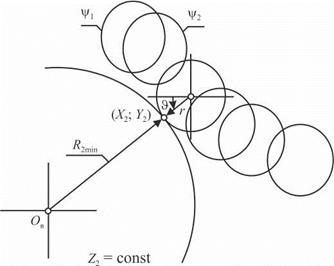
Геометрическую сущность метода численного профилирования поясняет рис. 5.12. В торцевой плоскости валка Z2 = const, находят следы ее пересечения деталью при различных углах у. Независимым параметром при этом является только угол Ф, так как последнее уравнение (3.39) позволяет установить его связь с параметром 1,. Затем по итерационной процедуре определяют радиус валка R2min как минимальное расстояние от его центра 0в до точек пересечения детали с плоскостью.
|
Рис. 5.12. Схема определения радиуса валка при численном профилировании |
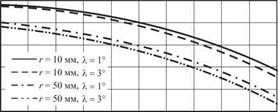
Для определения наладочного параметра а можно воспользоваться номограммой (рис. 5.13), где в зависимости от соотношения L/R приведены допустимые значения параметра а в процентном отношении от радиуса R бомбины для диапазона Le [0; 800], Re [800; 3000] мм. При этом не следует выбирать длину валков (участков валка) больше, чем радиус бомбины.
a/R, %
100 95 90 85 80 75
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
L/R
Рис. 5.13. Номограмма для определения параметра наладки а
Пример расчета профиля валков для наладок, используемых на станках SZASLE (Mikrosa, Германия), приведен в табл. 5.4 и на рис. 5.14. Исходные данные: r = 10 мм; R = 1000 мм; X = 1,5°; v = 30,0 мм; а = 975 мм; L = 400 мм (одноволновые), L = 600 мм (многоволновые).
Профиль одноволнового валка
для обработки бомбинированных деталей
|
Таблица 5.4
|
|
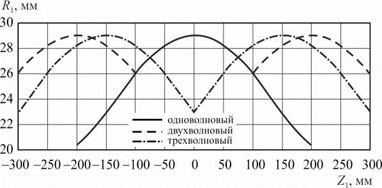
Рис. 5.14. Профиль валков для обработки бомбинированных поверхностей |
В общем случае профиль валка несимметричен относительно плоскости Z2 = 0 как для одно-, так и для многоволновых валков. Однако для реальных наладок станка (R > 300 мм, X < 3°, L < 800 мм) отклонения в точках профиля с противоположными координатами составляют несколько микрометров. Поэтому с позиции простоты изготовления профиль валков для обработки бомбинированных поверхностей можно считать симметричным относительно плоскости Z2 = 0. При этом оба валка имеют одинаковый профиль. Для многоволновых валков все участки его профиля (волны) также симметричны.
На рис. 5.15 дан график зависимости угла у от координаты Z2 валка. Анализ этого графика, характерного для различных сочетаний размеров заготовки и наладочных параметров суперфинишного станка, позволяет утверждать о линейной зависимости. Причем в сечении Z2 = 0 выполняется соотношение у = X. Установленный факт позволяет оптимизировать процедуру численного профилирования.
Большое значение при численном профилировании имеет дискретность задания угла у. Исследования показали, что при точности определения координат профиля валка 0,1 мкм можно ограничиться точностью задания угла у, равной 0,05°. Приведенная рекомендация позволяет уменьшить затраты машинного времени при итерационной процедуре поиска минимального радиуса валка в торцевом сечении.
Z2, мм
Рис. 5.15. Зависимость угла у от координаты Z2
Рассмотрим влияние основных параметров процесса формообразования на расчетный профиль валка для обработки бом — бинированных поверхностей.
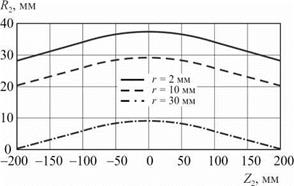
Радиус r заготовки практически не влияет на профиль валка, изменяя при прочих равных условиях только максимальный радиус валка (рис. 5.16). Исходные данные: R = 1000 мм; X = 1,5°; v = 30,0 мм; а = 975 мм; L = = 400 мм при r = 2; 10; 30 мм.
|
Рис. 5.16. Влияние радиуса r заготовки на профиль валков при обработке бомбинированных поверхностей |
Угол X перекрещивания осей валков в пределах 0…30 мало влияет на профиль валка. В табл. 5.5 представлены профили валков, рассчитанные для параметров r = 10 мм; R = 1000 мм; v = 30,0 мм; а = 975 мм; L = 400 мм при X = 0; 3°.
|
Таблица 5.5 Влияние угла перекрещивания осей на профиль валков
|
Наибольшее влияние на профиль валка оказывает радиус R траектории движения заготовок. Установлено, что увеличение радиуса R при прочих равных условиях приводит к уменьшению кривизны профиля и разности максимального и минимального радиусов валка.
|
Рис. 5.17. Обработка бомбинированных роликов на бесцентровом суперфинишном станке модели SZASLE-50×500 |
Методика расчета профиля валков бесцентрового суперфинишного станка модели SZASLE-50X500 для обработки роликов с модифицированной бомбиной 024×24 и 026×26 для подшипников 2319КМ, 2320М, 32319М, 42415М прошла опытную проверку на ОАО «Саратовский подшипниковый завод» (рис. 5.17). Испытания показали, что обеспечиваются точность диаметра в пределах 0,01 мм, радиус бомбины R5000-1000, несимметричность бомбины по диаметру — не более 0,01 мм.