Валковые устройства для обработки конических поверхностей

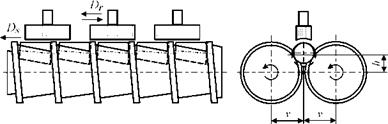
При обработке конических поверхностей валковая система бесцентрового суперфинишного станка (рис. 5.3) включает два параллельных валка с винтовыми канавками, один из которых является ведущим, а другой — поддерживающим (рис. 5.4).

Рис. 5.3. Схема суперфиниширования конических поверхностей деталей

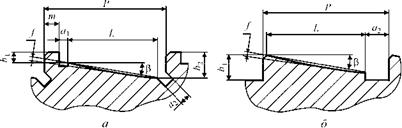
Рис. 5.4. Валки для суперфиниширования конических поверхностей: а — ведущий валок; б — поддерживающий валок

Заготовки ориентированы на валках образующей конуса па­раллельно направлению осцилляции шлифовальных брусков.

Винтовая поверхность валка состоит из двух частей, которые формируют коническая и торцевая поверхности заготовки. При этом часть винтовой поверхности валков, образованную кониче­ской поверхностью и предназначенную для базирования загото­вок, назовем рабочей, а другую часть винтовой поверхности, образованную основаниями усеченного конуса — вспомогатель­ной. Продольное перемещение производит боковой участок вспомогательной поверхности валка, контактирующий с боль­шим основанием конуса заготовки.

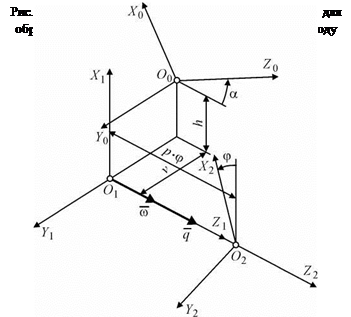
Введем в рассмотрение следующие координатные системы (рис. 5.5): S0(X0 О0 Y0 Z0) — система заготовки; S1(X1 О1 Y1 Z1) —

вспомогательная условно неподвижная система; S2(X2 О2 Y2 Z2) — система валка. Система координат S1 по отношению к системе S0 повернута вокруг оси Y против часовой стрелки на угол а и смещена на величину v по оси Y и на величину h по оси Х. Вин­товое движение задают параметрыр и ф в системе S2. На рис. 5.5 показана правая винтовая линия. В связи с равенством угла об­разующей конуса и угла перекрещивания осей конической заго­товки и валков из условий формообразования в дальнейших расчетах они имеют одинаковое обозначение а.

Поверхность валка определим как совокупность линий кон­такта заготовки и валка при их относительном винтовом движении. Для нахождения характеристики необходимо совместить коорди­натную систему S0 с системой S2 и выделить контактные линии по кинематическому условию. Винтовая поверхность, образованная конусом при перекрещивании осей, является нелинейчатой.

Коническую поверхность заготовки опишем в параметриче­ском виде следующими уравнениями:

Х0 = u sin а cos ф;

Y0 = u sin а sin ф; >

Z0 = rctga — u cos a,

где u, ф — криволинейные координаты конической поверхности; r — радиус основания конуса; a — угол образующей конуса.

Торцевую поверхность заготовки опишем как поверхность круга следующими уравнениями:

X0 = r cos ft; Y0 = r sin ft; > Z0 = Z

где rj, ft — криволинейные координаты круга; z — координата, за­дающая осевое положение круга.

Переход из системы S0 в систему S1 осуществим с помощью следующей матрицы:

cos а	0	sin а	h
0	1	0	—v
— sin а	0	cos а	0
0	0	0	1

Проекции единичного вектора нормали в соответствии с формулой (5.17) примут вид

nx = (cos2 a sin $ + sin2 a)cos ф + cos a cos $ sin ф; ny = -(cos2 asin $+sin2 a)sin ф + cos a cos $ cos ф;

nz = sin a cos a(1 — sin $).

Вектор скорости винтового движения определим по формуле

+ ч.	ЮУ ry	ю rz	л _ +j ■	( Чу +	Юх r	Ю r	л _ + к ■	( 4z +	Юх г	юУ " Г
V	У	z	У	V	х	z	У	V	х	у У

У

ГУ

+ ч-

= г

Без нарушения общности в выражении (5.19) примем ю = = 1 рад/с. Тогда имеем:

юх = 0; ay = 0; юг = 1. (5.20)

При этом проекции вектора поступательного движения

qx = 0; qy = 0; qz = р.

В окончательном виде кинематическое условие (cos2a sin ft+ sin2 a + h)(u sin a cos ft — v) — — (cos a cos ft — v)(0,5u sin 2a sin ft+

+ (Rctga — u cos a) sin a + h) +

+ [pep + 0,5 sin 2a(1 — sin ft)] = = 0.

Уравнение (5.22) содержит три независимых параметра u, ft и p, поэтому не может быть решено в явном виде. Для опреде­ления поверхности валка необходимо совместное решение уравнений (5.10), (5.14) и (5.22) с использованием параметриче­ской оптимизации.

Однако если кинематическое условие составить в системе ко­ординат, связанной с заготовкой, то угловой параметр p винтового движения в него не войдет, что упростит решение. При этом тре­буется выбрать системы координат таким образом, чтобы одна из осей системы заготовки была направлена по кратчайшему межосе­вому перпендикуляру. Аналогичный подход использован в [46], поэтому ограничимся выводом формул без подробных пояснений.

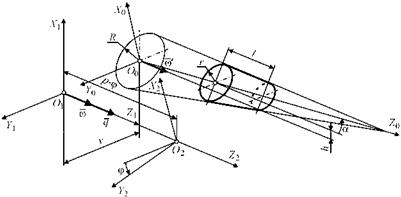
Введем в рассмотрение следующие координатные системы (рис. 5.6): S0(X0 О0 Y0 Z0) — система заготовки; S1(X1 О1 Y1 Z1) —

вспомогательная условно неподвижная система; S2(X2 О2 Y2 Z2) — система валка. Система координат S1 по отношению к системе S0 повернута вокруг оси Y против часовой стрелки на угол a и смещена по оси Y на величину v. Заготовка описана в виде усе­ченного конуса длиной l, расположенного на расстоянии h по оси Х в системе координат S0.

Коническую поверхность заготовки опишем в параметриче­ском виде следующим образом:

X0 = u sin a cos ft;

Y0 = u sin a sin ft; )

Z0 = Rctga — u cos a,

где R — радиус основания продолженного конуса, R = r + h/cosa.

В координатной форме уравнения семейства поверхностей валка:

X2 = (X0 cos а + Z0 sin а) cos ф + (Y0 — v) sin ф;

Y2 = —(X0 cosa + Z0 sina)sinф + (Y0 — v)cosф; > Z2 = —X0 sin a + Z0 cos a — рф — h / tga.

Относительное движение заготовки и валка определено скользящим вектором угловой скорости w и свободным векто­ром поступательного движения q. В результате приведения вектора w к точке О0 с помощью замены w’ = ю дополнительно появляется вектор-момент m (ю) = R • ю. Тогда выражение для скорости относительного движения примет следующий вид:

V0 = wr + m(w) + q,

где r — радиус-вектор текущей точки конической поверхности; R0 (0; v; 0) — радиус-вектор точки приложения скользящего век­тора ю.

Кинематическое условие в окончательном виде:

(Rctga cos a — u )sin a sin Ф + (v cos a — p sin a)cos a cos Ф+
+ (v sin a — p cos a)sin a = 0.

Уравнение (5.26) относительно параметра Ф является транс­цендентным, однако его можно преобразовать в квадратное уравнение, введя замену переменной:

(p sin 2a — v cos 2a)tg2 — +

Ф

+ 2 sin a(Rctga cos a — u)tg— + v = 0.

Уравнение (5.27) устанавливает связь между параметрами и и Ф. Данное уравнение имеет два решения, соответствующие двум контактным линиям.

Совместное решение уравнений (5.23), (5.24), (5.27) с секу­щими плоскостями позволяет получить осевое, торцевое или нормальное сечения валка. Осевое сечение поверхности валка получим, приняв Y1 = 0:

2 Ф

(p sin 2a — v cos2a)tg — +

Ф

+ 2sin a(Rctga cos a — и )tg— + v = 0; и sin a sin Ф-v

tg9 =———————————————— ;

и sin a cos a(cos Ф -1) + R cos a

X2 = (u sin a cos a(cos Ф -1) + R cos a)cos ф +

+ (u sin a sin Ф — v) sin ф;

Z2 = —u sin2 acos Ф+

+ (Rctga — u cos a) cos a — pф — h / tga.

Система уравнений (5.28) выражает в параметрической форме осевое сечение валка. Хотя в формулы входят перемен­ные u, Ф и ф, но так как две из них уже связаны кинематическим
условием, то независимых параметров только два. Поэтому ре­шение находят относительно переменных ft и ф при фиксиро­ванных значениях параметра u = R/sina — z/cosa, где координата ze [h/sina; h/sina + /].

Аналогичным образом получено кинематическое условие для торцевой круговой поверхности заготовки:

Анализ уравнения (5.29) показал, что для реальных наладок суперфинишного станка v + pctga > r и контактная линия рас­полагается вне круговой поверхности заготовки радиуса г. По­этому формировать вспомогательную часть винтовой поверхно­сти валка будут окружности сопряжения конической и торцевых поверхностей заготовки. Переходная поверхность, образованная малым основанием усеченного конуса заготовки, функциональ­ного назначения не имеет.

Переходная кривая будет получена на валке, если сообщить окружности основания конуса в системе S0 винтовое движение (осевое сечение):

Г sin ft — v

^ф=———— !———:—;

Г cos a cos ft+ zi sin a

X2 = (r cos a cos ft + zt sin a)cos ф + (rj sin ft — v) sin ф; Z2 = —j sin acos ft + z cos a — рф — h / tga,

где r — радиус круговинтовой линии, r = R — zt tga; zt — коорди­ната круговинтовой линии.

Построение круговинтовых линий также дало возможность рассмотреть и рабочую часть винтовой поверхности валка, а их совместный анализ в общей системе координат позволил оце­нить характер сопряжения и сформировать винтовую поверх­ность в целом.

Таким образом, поверхность валка для обработки конических поверхностей представляет собой нелинейчатую винтовую по­
верхность, включающую рабочий участок, обеспечивающий бази­рование заготовок при обработке, и вспомогательный, обеспечи­вающий продольную подачу. Рабочий участок валка определяют по формулам (5.28) на основе кинематического условия касания поверхностей, а вспомогательный участок — по формулам (5.30) как след, оставленный круговинтовыми линиями окружностей со­пряжения конической и торцевых поверхностей заготовки.

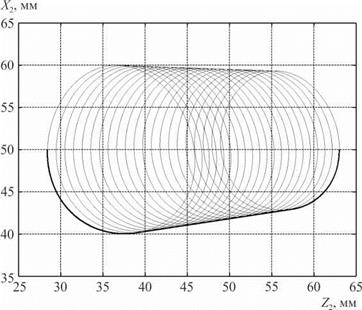
В табл. 5.3 и на рис. 5.7 приведен пример расчета осевого се­чения валка для следующих исходных данных: r = 10 мм; а = 5°; l = 20 мм; p = 40 мм; h = 30 мм; v = 40 мм.

В общем случае рабочий участок осевого сечения валка полу­чается криволинейным. Оценить такой профиль валка можно, используя угол профиля в и стрелу прогиба f (см. рис. 5.4). Прак­тическое значение также имеет ширина переходных кривых h1 и h2, которая определяет дополнительные участки профиля а1, а2 и шаг р винтовой поверхности валка. Для приведенного примера получе­ны параметры профиля: в = 8°36’6"; f = -0,004 мм; h1 = 10,4 мм; h2 = 5,6 мм (табл. 5.3).

Таблица 5.3

Осевой профиль валка для обработки конических поверхностей

Но­ мер- точ­ ки	Параметры	Коорд про<	инаты иля	Но­ мер точ­ ки	Параметры	Коорд про<	инаты иля
Ф, град	и, мм	Z2, мм	X2, мм	Ф, град	и, мм	Z2, мм	X2, мм
1	42,5	—	28,452	49,998	13	—	106,707	46,297	41,225
2	54,7	—	28,596	47,877	14	—	104,699	48,142	41,504
3	66,9	—	29,155	45,810	15	—	102,691	49,987	41,783
4	79,1	—	30,154	43,903	16	—	100,684	51,833	42,063
5	91,3	—	31,589	42,269	17	—	98,676	53,680	42,343
6	103,5	—	33,414	41,019	18	—	96,668	55,528	42,624
7	115,7	—	35,531	40,247	19	—	94,661	57,376	42,904
8	127,9	—	37,788	40,016	20	142,77	—	58,373	43,135
9	—	114,737	38,927	40,114	21	156,91	—	60,144	44,005
10	—	112,730	40,768	40,391	22	171,05	—	61,551	45,355
11	—	110,722	42,610	40,669	23	185,19	—	62,504	47,066
12	—	108,714	44,453	40,947	24	199,33	—	62,973	49,003

Рис. 5.7. Профиль валка для обработки конических поверхностей

Рассмотрим влияние основных параметров формообразова­ния на профиль осевого сечения валка для обработки кониче­ских деталей.

Проведенный численный анализ установил, что для реаль­ных наладок суперфинишного станка рабочий и вспомогатель­ный участки осевого профиля валка имеют плавное сопряжение с одной точкой контакта.

Профиль рабочего участка валка криволинейный, характер­ная форма — вогнутость в пределах f = —0,001 —0,01 мм для ис­

пользуемых наладок станка. Выпуклый профиль наблюдается лишь в случаях h > v и при больших углах а, что не свойственно суперфинишированию конических деталей. Угол профиля в валка всегда больше, чем угол а конической детали, и обычно удовлетворяет соотношению в = (1,5_2)а.

Наибольшее влияние на профиль рабочего участка оказы­вают следующие параметры: угол а конической заготовки (угол перекрещивания осей валка и заготовки), шаг р винтовой по­верхности и соотношение h/v вертикальной и горизонтальной наладочных координат станка.

Увеличение угла а приводит к увеличению параметров профиля в и f причем увеличивается не только абсолютная ве­личина угла профиля в, но и соотношение в/а. Увеличение шага р или соотношения h/v ведет к одновременному увеличению уг­ла в и уменьшению стрелы прогиба f При некоторых соотноше­ниях h/v профиль валка будет прямолинейным (f = 0) в доста­точно широком диапазоне изменения угла а.

Ширина переходных кривых зависит от тех же параметров, что и профиль рабочего участка. Шаг р винтовой поверхности и радиус r основания конической заготовки однозначно влияют на параметры h и h2 — при их увеличении они также увеличивают­ся. С ростом угла а ширина переходной кривой большего торца hi возрастает, а меньшего торца h2 — убывает. Повышение соот­ношения h/v приводит к одновременному увеличению ширины обеих переходных кривых.