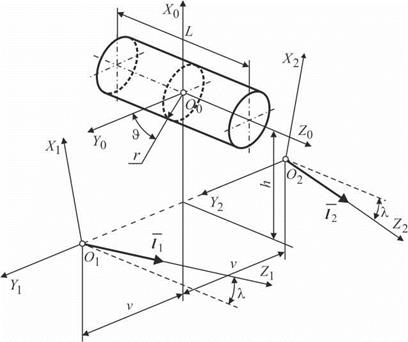
Поверхность валков определим как тела вращения, непрерывно касающиеся виртуального цилиндра заготовок (потока цилиндрических заготовок). Введем в рассмотрение следующие координатные системы (рис. 5.1): S0(X0 О0 Y0 Z0) — система заготовки; S1(X1 О1 Y1 Z1) и S2(X2 О2 Y2 Z2) — системы левого и правого валков соответственно. Системы координат S1 и S2 по отношению к системе S0 повернуты вокруг оси Y по и против часовой стрелки на угол X и смещены по оси X на величину h и по оси Y на величины — v и v соответственно.
Наладочную координату h не устанавливают непосредственно на станке, а получают при заданной геометрии валка, радиусе заготовки и наладочных координатах v, X. Поэтому вместо координаты h целесообразно задавать так называемый «номинальный» радиус R валков в точке перекрещивания. В результате значение h будет определено очевидным образом.
Поверхность цилиндрической заготовки в векторно-параметрической форме в системе S0 опишем уравнением
r0 =-r sin Ь-i + r cos j + z-k, (5.1)
где r — радиус заготовки; Ф, z — криволинейные координаты цилиндрической поверхности.
|
Рис. 5.1. Координатная схема профилирования валков при обработке цилиндрических поверхностей |
Для преобразования координат поверхности заготовки из системы S0 в систему Si воспользуемся матричным равенством:
ri = M10 ■ r0, (5.2)
где М10 — матрица перехода из системы координат S0 в систему S1. Матрица перехода М10 имеет вид
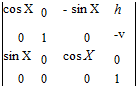 (5.3)
(5.3)
где X — угол перекрещивания осей валка и заготовки; 2v — межосевое расстояние валков; h — вертикальная наладочная координата станка.
В проекциях уравнения, описывающие семейство поверхностей левого валка S1, принимают следующий вид:
![]() X1 = — r sin ftcos X-z sin X + h cos X; Y1 = r cos ft-v; )
X1 = — r sin ftcos X-z sin X + h cos X; Y1 = r cos ft-v; )
Z1 =-r sin ftsin X + z cos X + h sin X.
Для определения искомой поверхности валка по уравнениям (5.4) необходимо найти контактную линию. С учетом наличия осей зацепления составим кинематическое условие в виде определителя, аналогичного изложенному в [43].
Для левого валка кинематическое условие, составленное в системе координат S0, имеет вид
|
h — r sin ft |
r cos ft-v |
z |
||
|
— sin ft |
cos ft |
0 |
= 0. |
(5.5) |
|
sin X |
0 |
cos X |
Из выражения (5.5) установим связь между криволинейными координатами ft и z:
Уравнение (5.6) относительно угла Ф имеет два решения — Ф1 и Ф2, что формально связано с периодичностью функции тангенса. Геометрический смысл заключается в том, что на поверхности цилиндра в заданном сечении есть две контактные точки, нормали в которых пересекают ось валка, при этом Ф2 = Ф1 + 180°.
Поверхность левого валка в окончательном виде опишется уравнениями:
Х1 = —r sin dcos X — z sin X + h cos X;
Y1 = r cos Ф — v;
![]() Z1 =— rsin$sinX + zcosX + hsinX; r
Z1 =— rsin$sinX + zcosX + hsinX; r
![]()
h — zctgX
v
Профиль валка как тела вращения целесообразно задавать в цилиндрической системе координатами (Z1, R), где R1 =
+ Y12 . Тогда последовательность расчета по формулам
(5.7) следующая. При фиксированном значении ze [-L/2; L/2] из последнего уравнения (5.7) находят криволинейную координату Ф, которую затем подставляют в выражения для X1; Y1; Z1 (L — длина валков).
Для дальнейшего изготовления и контроля валков в качестве фиксированного параметра при расчете удобно задавать непосредственно координату Z1 валка. Тогда для определения параметра Ф необходимо решить следующее трансцендентное уравнение:
r sin X sin Ф — (h — vtg Ф) cos XctgX + Z1 = 0. (5.8)
Аналогичным образом получены уравнения для правого валка:
X1 = — r sin $cos X + z sin X + h cos X;
Y = r cos Л+v;
![]() Zj =r sin $sin X + z cos X + h sin X; r
Zj =r sin $sin X + z cos X + h sin X; r
![]() ztgX-h
ztgX-h
v
Пример расчета профиля валков для наладок, используемых на станках SZZ-3 (Mikrosa, Германия), приведен в табл. 5.1. Исходные данные: r = 10 мм; R = 62,5 мм; X = 1,75°; v = 64,0 мм; h = 34,062 мм; L = 800 мм.
Левый и правый валки имеют одинаковый профиль, но развернуты в противоположных направлениях, поэтому они симметричны относительно плоскости Z1 = 0. Поверхность валка имеет форму, близкую к поверхности однополостного гиперболоида. Так, при радиусе заготовки, равном нулю, цилиндр превращается в прямую и образует однополостный гиперболоид. Таким образом, полученную поверхность валка можно назвать квазигиперболоидом. Форма таких валков и способ их изготовления запатентованы [45].
|
Таблица 5.1 Профиль валков для обработки цилиндрических поверхностей
|
Рассмотрим влияние основных параметров процесса формообразования на изменение расчетного профиля валка.
Увеличение угла X перекрещивания осей валка и заготовки приводит к увеличению кривизны валка и разности его максимального и минимального радиусов. Данный факт нежелателен
как с точки зрения кинематики процесса, так и трудоемкости изготовления валка. С другой стороны, угол X вместе с окружной скоростью валка определяют продольную скорость заготовок. Поэтому при проектировании следует назначать минимальную величину исходного угла перекрещивания осей валков при обеспечении требуемой продольной скорости заготовок.
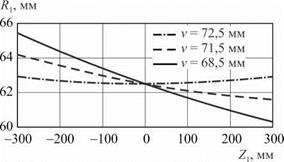
Изменение наладочных координат v, h суперфинишного станка при постоянном номинальном радиусе R валка приводит к идентичным результатам. При уменьшении v (или увеличении h) профиль валка меняется таким образом, что увеличивается разность его максимального и минимального радиусов. В табл. 5.2 и на рис. 5.2 представлены результаты расчета профиля валков для исходных данных: r = 10 мм; R = 62,5 мм; X = 1,5°; L = 600 мм. При этом изменялось значение v = 72,5; 71,5; 68,5 мм, которому соответствовали h = 0; 12,0; 23,749 мм.
Таблица 5.2
Изменение профиля валка в зависимости
от межосевого расстояния v
|
R1, мм |
v, мм |
Z1, мм |
|||||
|
-300 |
-200 |
-100 |
0 |
100 |
200 |
300 |
|
|
72,5 |
62,924 |
62,689 |
62,547 |
62,500 |
62,547 |
62,689 |
62,924 |
|
71,5 |
64,206 |
63,548 |
62,979 |
62,500 |
62,113 |
61,819 |
61,620 |
|
68,5 |
65,439 |
64,380 |
63,399 |
62,500 |
61,684 |
60,957 |
60,319 |
|
Рис. 5.2. Влияние наладочного параметра v на профиль валка |
Из рис. 5.2 видно, что при h = 0 профиль валка симметричен относительно плоскости Zi = 0. При увеличении h поверхность валка представляет собой часть поверхности квазигиперболоида, расположенную на соответствующем расстоянии от точки перекрещивания.