Расчет температурных полей поверхности детали. разных сталей в зоне шлифования

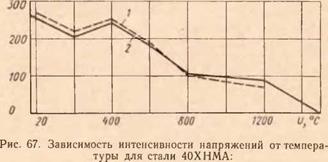
В соответствии с методикой расчета на ЭВМ температур­ного поля зоны шлифования, изложенной выше, необ­ходимо построить ряд экспериментальных графиков и аппроксимировать соответствующие этим графикам функ­ции для ввода их в программу ЭВМ. В частности, необ­ходимо построить графики и получить по ним аналити­ческие зависимости влияния температуры на теплофизи­ческие свойства металлов (для учета внешней нелиней­ности), на сопротивление сталей разных марок пласти­ческому деформированию (для учета внутренней нелиней­ности) и построить график безразмерного критерия П (б), являющегося характеристической функцией тем­пературного поля детали в зоне шлифования.

Так как все исследуемые на обрабатываемость шлифо­ванием марки сталей и сплавов были разбиты ранее на пять групп, с объединением внутри каждой группы ста­лей, близких по обрабатываемости и приближенно по структурно-химическому составу, то построение соответ­ствующих графиков и вывод аналитических зависимостей будет производиться только для характерных представи­телей: группа углеродистых сталей — У10; группа леги­рованных конструкционных сталей — 40ХНМА; группа хромистых сталей— 1X13; группа хромоникелевых спла­вов— Х18Н10Т; группа быстрорежущих сталей—Р18.

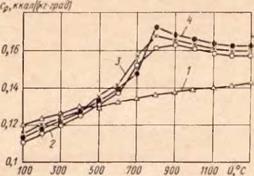
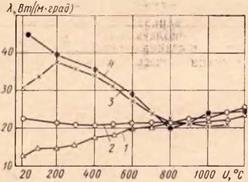
Вывод зависимости влияния температуры на теплофи­зические свойства металлов. График изменения от темпе­ратуры теплоемкости разных сталей (представителей раз­ных групп), построенный по справочным данным, приве­ден на рис. 57. Для хромистых и быстрорежущих сталей 1X13 и Р18 (кривая 2), легированных (стали 40ХНМА и ЗОХГСНА — кривая 3) и углеродистых (сталь У10 — кривая 4), зависимость ср—U близка по характеру кри — 162

пых и по абсолютным значениям ср для разных значений U. Мри этом в зоне U = 800° С на графике для всех трех ірупп сталей наблюдается перелом кривых.

Рис. 57. Влияние температуры на изменение тепло­емкости разных сталей по справочным данным (/ — X 18НІ0Т; 2 — Р18; 3 — 40ХНМА; 4 — У10)

Четвертая группа — хромоникелевые (аустенитные) сплавы (сталь Х18Н10Т — кривая 1) имеет линейную за­висимость ср—U с малым углом наклона. Усреднением по

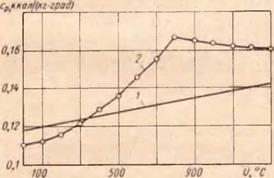
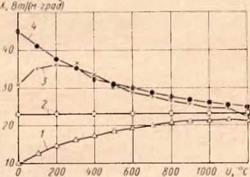
Рис. 58. Аппроксимация зависимости теплоемкости от температуры (/ — сталь Х18Н10Т; 2 — другие стали)

всем известным точкам выбраны параметры линейной зави­симости, после чего аппроксимирующая функция для хромо­никелевых сплавов (сталь Х18Н10Т) приняла вид (рис.58) с. = 0,19Ы0-2{У + 0,118. (64)

Так как приведенные на рис. 57 кривые ср—U для сталей трех других групп являются статистическими со значи­тельным интервалом рассеивания, целесообразно их объединить в одну. При аппроксимации кривых 2, 3, 4 (см. рис. 57) некоторой функцией нужно учесть вероят­ность того, что при расчете может понадобиться темпера­тура, выходящая за пределы 1300° С. Из анализа кривых (рис. 57) можно предположить, что при более высокой температуре (>1300° С) значения ср остаются постоян­ными. Следовательно, при аппроксимации нужно преду­смотреть у искомой функции наличие горизонтальной асимптоты при U > 1300° С.

Усредняя кривые 2, 3 и 4 в одну (рис. 58), получим

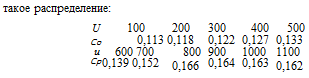Так как в зоне U = 800° С наблюдается излом кривых 2, 3 и 4 (см. рис. 57), для упрощения получаемых функций целесообразно провести аппроксимацию кусочно: до

U = 800° С одним аналитическим выражением, а для U > 800° С — другим.

Для получения более простого выражения необхо­димо, чтобы график проходил через начало координат, для этого надо вычесть ср =0,11. Тогда

U 100° 200° 300° 400° 500° 600° 700° 800°

Ср — 0,11 0,003 0,008 0,012 0,017 0,023 0,029 0,042 0,056

Покажем, что кривая, определяемая функцией вида

У = ахь, (65)

при соответствующем подборе параметров довольно точно аппроксимирует ломаную. Проверим, может ли функция у = ахь аппроксимировать данную ниже зависимость.

Логарифмируя уравнение (65), получим

lg У = b lg л: + lg а.

В координатах lg х, lg у эта зависимость линейна: Y = Ьх + lg а, (66)

где Y = lg у, X = lg л:.

Рассмотрим зависимость ср— U (табл. 11) в коорди­натах, описанных уравнением (66).

164

1/ и °С	ср-0М	lgt;	— —0,11)	и в °С	Vой	lg и	lg (с — -0,11)
100	0,003	2	—2,5229	500	0,023	2,6990	— 1,6383
200	0,008	2,3010	—2,0969	600	0,029	2,7782	— 1,5376
:юо	0,012	2,4771	— 1,9208	700	0,042	2,8451	— 1,3768
-100	0,017	2,6021	— 1,7636	800	0,056	2,9031	— 1,2518

Таблица 11

Зависимость ср — U

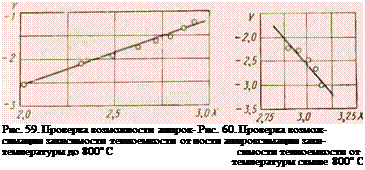Построим зависимость в координатах XY. Из графика (рис. 59) видно, что точки располагаются по линейной зависимости, т. е. кривая, описанная уравнением (65), пригодна для аппроксимации рассматриваемой функ-

ции ср — U. Определяя из рис. 59 параметры линейной зависимости, имеем

Y = 1,5814* — 5,8428,

т. е. b = 1,5314, lga = —5,8428, а = 0,1436 • КГ4. Следовательно,

ср = 0,1436- ІСґД/1-5814 + 0,11 (0<; £/ ==£; 800°С). (67)

Для аппроксимации второго участка нужно выяснить, к какой асимптоте будет стремиться ср — U при U —* оо. Из рис. 57 можно заключить, что уравнение асимптоты будет иметь вид ср — 0,16. Тогда вычитая асимптоту,

165

получим следующее табличное задание аппроксимируе­мой зависимости:

U………………. 800°С 900°С 1000°С 1100°С 1200°С

ср — 0,16 • • 0,006 0,005 0,003 0,002 0,001

Аппроксимирующую кривую можно выбрать из класса кривых, имеющих нулевую асимптоту при U-• оо: ср = аи~ь. Проверка в координатах X=|g£7, Y = lgc„

показывает, что эта функция вполне пригодна для аппрок­симации данной функциональной зависимости (рис. 60):

X Ig (/…………………….. 2,9031 2,9542 3,0000 3,0414 3,0792

Y lg (Ср — 0,16) ■ • —2,2218 —2,3010 —2,5229 —2,6990 —3,000

Определяя из рис. 60 параметры линейной зависимости, имеем

Y = —3.4505Х + 7,7953.

Перейдя к координатам ср U, получим

ср = 6,237 . ЮЧ/"3-‘*» + 0,16 (U > 800°С). (68)

Для углеродистых, легированных, хромистых и быстро­режущих сталей имеем

| 0,1436-И) и* ‘ли —[- 0,11; 0<t/^800°;

Ср= 6,237-7U~3-4505 0,16); 800° < U,

а для хромоникелевых сплавов

Ср — 0,191.10-а(У + 0,118.

График изменения от температуры коэффициента теп­лопроводности разных сталей, построенный по справоч­ным данным, приведен на рис. 61. Из графика видно, что 166

псе четыре группы имеют различный характер изменения коэффициента теплопроводности в зависимости от темпе­ратуры. Учитывая статистический характер представлен­ных кривых (средние значения для нескольких сталей данной группы), можно принять для хромистых и быстро­режущих сталей А, = const. Так как все кривые имеют явную тенденцию к сближению и после U = 800° С прак­тически сливаются в одну, можно считать, что все они имеют общую горизонтальную асимптоту на уровне хро­мистых и быстрорежущих сталей, для которых X = 23.

Для выявления особенностей функциональных зави­симостей и упрощения задачи подбора аппроксимирую­щих функций «вычтем» асимптоту из кривых графика (рис. 61). Применяя методику расчета, аналогичную изложенной выше, получим: для углеродистых сталей I = 22,ЗЭ^0-*07 I(W + 23;

для легированных конструкционных сталей к = = 0,148 (U + 50) е " ‘-‘ (с/+ 50) | 23;

для хромоникелевых аустенитных сплавов X = 23 •— 13 е — °’0(Ш.

На рис. 62 даны кривые, построенные по полученным функциям. Таким образом, для всех групп сталей спра­вочные зависимости ср (U) и X (U) аппроксимированы аналитическими функциями для последующего ввода их в программу ЭВМ. Сравнение справочных данных ср и X с аппроксимирующими их функциями показало, что абсолютные отклонения расчетных кривых лежат в пре­делах ср ^ ±5%, X = ±5%.

Математическая обработка экспериментальной зависи­мости влияния температуры на сопротивление сталей пла­стической деформации шлифованием. Количество тепла, выделяемого при резании нагретого металла, будет за­

сгруппированные по химическому составу и структурному сходству сталей (приближенно). Из графиков видно, что выводить единую усредненную зависимость а, (U)

е1 шл

для сталей каждой группы нецелесообразно, так как при сохранении приближенного вида кривой внутри каждой группы разные стали значительно отличаются друг от друга ординатами. Поэтому выберем представителей от каждой группы и ограничимся выводом аналитических

1 — экспериментальная; 2 — приближенно-расчетная

зависимостей а, (U) и расчетом температурных полей

£/шл

для отдельных сталей — представителей этих групп: углеродистые—У10А; легированные конструкцион­ные— 40ХНМА и ЗОХГСНА; хромистые— 1X13; бы­строрежущие— Р18; хромоникелевые— Х18Н10Т. Экспериментальные зависимости и (U) для этих

£1ШЛ

сталей имеют неудобный для аналитической аппроксима­ции вид. Задача усложняется еще тем, что для температуры, превышающей точку плавления (U > Нпл), сопротивле­ние пластическому деформированию очевидно пренебре­жимо мало, т. е. нужно обеспечить при аппроксимации нулевые асимптоты при U—> оо. При этом для U >■ U„„ значения а, должны быть весьма малы.

£ішл

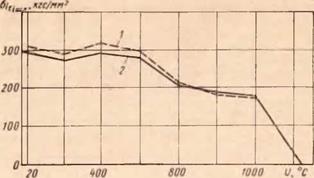
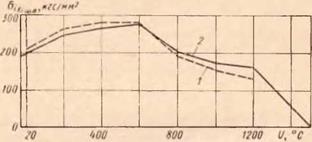
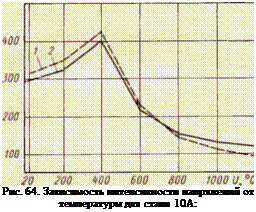
Рис. 65. Зависимость интенсивности напряжений от тем пературы для стали Р18:

/ — экспериментальная; 2 — приближенно-расчетная Рис. 66. Зависимость интенсивности напряжений от темпе­ратуры для стали 1X13:

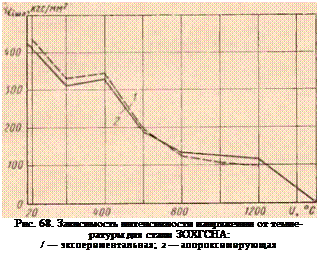
/ — экспериментальная; 2 — аппроксимирующая бц^кге/ни? 1 — экспериментальная; 2 — аппроксимирующая

При последующей аппроксимации широко исполь­зовались наложения более простых (чем заданная) за­висимостей и методика, примененная при получении функ­ции ср (U), описанная выше. Ниже приводятся только результаты аналитической и графической аппроксимации функций af (U) для разных сталей. Так, экспери-

е/шл

ментальная и приближенно-расчетная зависимость о,- (U) для стали У10А имеет вид, как на рис. 64.

г/шл

Приближенно-расчетная зависимость имеет вид

о — = ЗбОе-0’128-10-* 4-

‘Ч шл (УІ0А)

— 250е-о. и-м-ч/ і іЗОе-о. ооі-ю-» (i/-woo)*

Результаты аппроксимации остальных исследованных сталей приведены на рис. 65—69. Кривые 2 этих графиков построены по следующим функциям:

_j_ 1 I 64»-°.л-,и’* (£/—П50)« 95g-2.28.10-*и.

о,- = 252,9e~°‘12’10~’u — f-

<е/ шл (40XHMA) 1

+ 0I032e3-,0_,t/-3-10-*1′ + 0,13 • 10- (73)

a. = 424,9t»-o. i6.io-i/ .

,{Ч шл (30ХГСНА) ’

-f — 89,5e-1•28+0’64•10-2£;-0•08■10■*c;, j
-f 24,7c_ч•в8+I•6,i•I0**t/-0•IД•,<,■*t/, -f-
+ 57ile~63’36+0-105t/-M4’10_4£/-

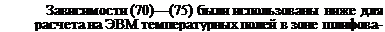
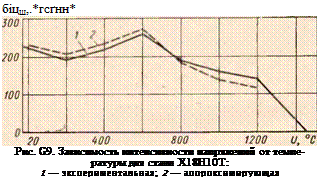
= 143,5е~10_*° (£/—600)’« +

ния на поверхности сталей шести перечисленных марок (представителей пяти различных групп сталей) и позво­лили более правильно учесть сопротивление деформи­рованию срезаемых и еще не остывших слоев металла в зоне резания и тем самым более точно и правильно опре­делить при расчете температуры интенсивность тепловых источников — зерен. Без такой поправки интенсивности тепловых источников оказываются сильно завышенными.

Задание для ЭВМ и результаты расчета температурных полей шлифуемой поверхности для различных сталей и условий шлифования. При анализе температурного поля зоны шлифования рациональным способом представления 172

искомой функции U (a, t) является графический. Но так как эта функция двумерна, ее геометрическая интерпре­тация (при двух текущих значениях аргумента) неудобна.

Учитывая, что нас интересует распределение U (a, /) по глубине а в довольно малых пределах (от 0 до 10 мкм), то в тонком поверхностном слое можно взять несколько дискретных глубин и рассмотреть процесс во времени Ua (/) на этих глубинах. Для расчета были взяты глубины, равные 2, 5 и 10 мкм (среднее значение толщины срезае­мого слоя одним зерном для исследуемых условий состав­ляет порядка 5 мкм).

Так как количество зерен круга, участвующих в ра­боте «друг за другом» на длине дуги контакта, в зависи­мости от характеристики круга может колебаться в зна­чительных пределах, расчет производили в нескольких вариантах для различного количества импульсов, дей­ствующих на участок поверхности от момента входа до выхода из контакта с кругом.

Выше было обосновано, что наиболее вероятное коли­чество зерен, работающих «друг за другом» (при различ­ной зернистости кругов и различной степени их затупле­ния), находится в пределах 8—20. Поэтому далее для расчета принимается количество импульсов 8, 12 и 20.

При одинаковой длине дуги контакта, принятой для расчета /; = 1,0 мм, время прохождения всей длины дуги контакта через зону шлифования равно (при уд = 20 м/мин

t[_ = = 0,003 с. Тогда шаг по времени h и

точки lt вводить массивом в память машины не нужно, их можно вычислить:

//=4*-з = i—(k — 1); а = h ^k—- ip) ;

/<+2=4*-і =h(k———— ;

Время действия теплового импульса при диаметре затупления вершины зерна 0,1 мм и при у* = 35 м/с со­ставляет 3 10"6 с.

Таким образом, для каждого k-ro импульса будем иметь четыре точки по времени в которых и будет вы­числяться температура для заданной глубины а. Вычисле­ние температуры в каждой точке (а it) производится по описанному выше алгоритму. Наглядное представление

tl

t

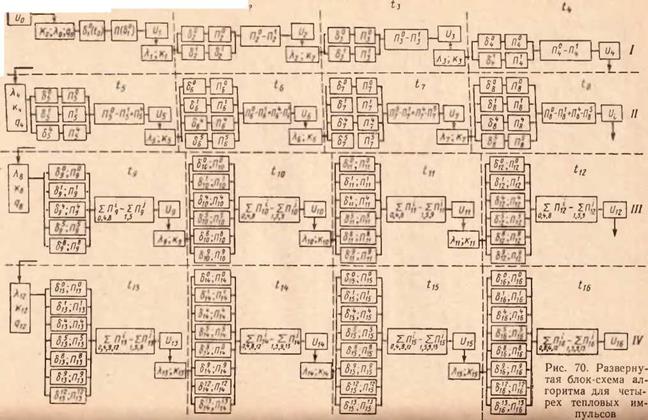
о характере счета участвующих в расчете факторов и структуре алгоритма дает развернутая блок-схема (рис. 70) для случая четырех импульсов и одной глубины а. Соответствующие значения а, X и q брали из выведенных в предыдущих пунктах функций с (U), А, (U) и о,. (U).

ЄІШЛ

В качестве Uо взята температура (/„ = 0° С (пренебре­гая разницей между 0° С и t/K0M = 18-^20° С).

Расчет производили на ЭВМ «Минск-22».

В результате счета были получены искомые значения U (Xj t,), по которым были построены приведенные ниже

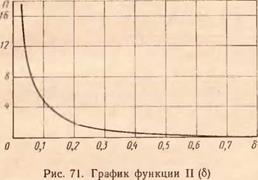
графики. Кроме того, получены значения безразмерного параметра 6* и соответствующие им функции П (б;). Это дало возможность построить график функции П (б) (рис. 71), по которому можно быстро (без программирова­ния и расчета на ЭВМ) определить температуру для ана­логичных тепловых процессов (другие /, х, п и пр.) по описанному выше алгоритму и приведенной блок-схеме. С использованием графических зависимостей о (U), с ({/), А, (U) можно также без ЭВМ производить ориенти­ровочный расчет температуры даже с учетом изменения теплофизических и прочностных свойств материала.

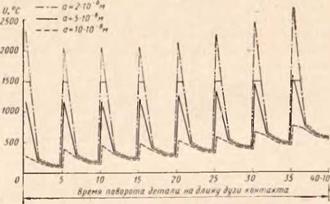
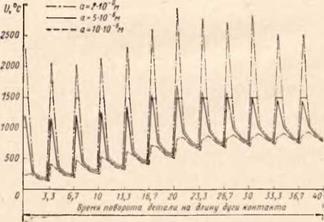
Результаты расчета температурных полей, действую­щих в поверхностных слоях детали (а — — 2, 5 и 10 мкм) в зоне шлифования для стали ЗОХГСНА, представленные в координатах «температура — время», приведены в виде графиков на рис. 72—74. Графики для сталей остальных марок имеют аналогичный вид, отличаются только уров­нем колебаний температурных полей и поэтому не приво-

Рис. 72 Изменение температуры при шлифовании стали ЗОХГСНА на различной глубине (а) от поверхности за время прохождения уча­стком детали длины дуги контакта (при восьми зернах-импульсах)

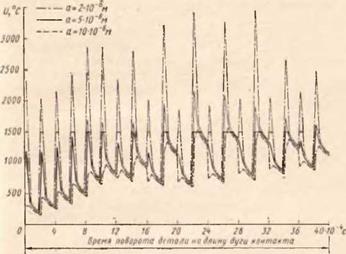
Рис. 73. Изменение температуры при шлифовании стали ЗОХГСНА на различной глубине (а) от поверхности за время прохождения уча­стком детали длины дуги контакта (при 12 зернах-импульсах)

дятся. По оси абсцисс графиков отложено время прохожде­ния точкой поверхности детали длины дуги контакта (в рассматриваемом случае L ~ 1,0 мм), т. е. время от момента входа малого участка поверхности детали в зону действия зерен круга до момента выхода из нее.

Поэтому на графиках, очевидно, следует обратить внимание на крайние точки (или линии) колебания тем-

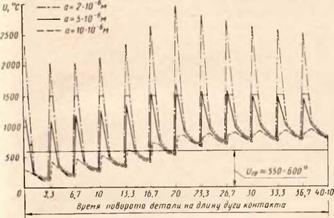
Рис. 74. Изменение температуры при шлифовании стали ЗОХГСНА на различной глубине (а) от поверхности за время прохождения уча­стком детали длины дуги контакта (при 20 зернах-импульсах)

пературного поля — максимальную и минимальную тем­пературы. Графики показывают температурное поле по времени нестационарно и иррегулярно, т. е. по времени температурные колебания перемещаются в область более высокой температуры.

Количество зерен, участвующих в работе, или коли­чество тепловых импульсов, также оказывает влияние на характер и расположение по оси U температурного поля. Поэтому в дальнейшем определение характерных темпе­ратурных величин производится для различного коли­чества импульсов и с учетом времени действия той или иной температуры. На графиках для стали ЗОХГСНА при­ведены данные расчета для 8, 12 и 20 импульсов, дей-

ствие которых наиболее вероятно для средних режимов круглого шлифования кругами средней зернистости (т. е. sBp 1—2 мм/мин, зернистость круга 25—50).

Вначале рассмотрим максимальную температуру (пики, образующиеся в момент окончания действия теплового импульса). Характерно, что для всех сталей эта темпера­тура для слоя а = 2 мкм (а для отдельных сталей и для слоя а — 5 мкм) превышает температуру плавления ме­таллов, что физически невозможно. Это проявление влия­ния одного из допущений, сделанных в расчетной схеме, а именно, что металл изотропен и при расчете не учиты­ваются фазовые превращения в нем в процессе распростра­нения тепла (скрытая теплота плавления).

Из графиков видно, что зона возможного расплавле­ния металла невелика (а 2 мкм, максимум до 5 мкм) и температура U /> £/пл столь кратковременна, что физи­ческого расплавления металла может и не наступить. В работах [6, 7, 31] описана методика эксперименталь­ного измерения температуры контакта абразивных зерен при шлифовании, в основу которой положен термоэлек­трический эффект, возникающий между материалом абра­зивных зерен из карбида кремния и шлифуемым металлом. Температура контакта по разработанной методике опре­делялась при шлифовании большой группы металлов и сплавов. Было установлено, что с повышением скорости температура непрерывно растет и, например, для стали 40 при скорости шлифования 20 м/с достигает температуры плавления. Для сплава BTI4 температура плавления достигается уже при скорости 15 м/с. После этих скоростей температура остается на уровне максимума, близкого к температуре плавления.

В расчетах температуры нагрева поверхности шлифо­вания детали в зоне контакта [51 ] температура также достигает и превышает точку плавления. На это же ука­зывается в работе [35]. Однако даже допущение, что возможно кратковременное расплавление малых объемов металла, существенно меняет математическую модель процесса распространения тепла в зоне шлифования, которая была использована в данном расчете. Необхо­димо в этом случае ставить для уравнения теплопровод­ности задачу Стефана, учитывающую фазовые превраще­ния в процессе распространения тепла.

В силу особенностей исследуемого процесса математи­ческое описание выглядит следующим образом. До момента 178

плавления слоев металла, прогретых до температуры плавления, имеем обычную задачу теплопроводности с ис­точником р (0, t) на границе х — 0:

^- = х1-^-(1)</<т1Л0<А-<со), (76)

где т — время появления слоев металла с температурой плавления.

С появлением прогретых до ипл слоев металла учиты­ваем фазовые превращения:

(т, </< :•-, 0 <*<£), (77)

а ниже g < х < оо, где U < U„„ продолжает действовать;

ОТ/,

dt — 1 дх* ‘

На границе фазовых превращений ставится условие

, dUt(lt) ^ dUy (I,/)
дх ~ А‘ дх

где (У, — температура твердой фазы;

U. — температура жидкой фазы;

/. і и — теплопроводность соответственно жидкой и твердой фаз;

g — координата фронта (по глубине) фазового перехода.

После окончания работы источника в результате охлаждения расплавленная зона выродится и процесс дальнейшего охлаждения будет описываться уравне­нием (76), но без источника. Это — существенно нелиней­ная задача, которая в этом случае не решается. Задача настоящего исследования заключается в определении температуры, до которой успевают охладиться снимаемые слои металла к моменту подхода очередного зерна круга.

Задачи Стефана заключаются главным образом в опре­делении объемов расплавленного металла, и возможной температуры его нагрева выше точек плавления. Решение такой задачи очень важно для исследований, связанных с определением качества поверхностных слоев шлифо­ванных деталей и возможных структурных изменений в поверхностных слоях.

По расчету максимальная температура, возникающая в тонких поверхностных слоях, физически может дости­гать температуры плавления, от которой и происходит остывание, ориентировочно описываемое принятой расчет­ной схемой.

Для оценки обрабатываемости сталей шлифованием необходимо знать минимальную температуру, до которой успевают остыть поверхностные слои в зоне резания. Сначала отметим несколько общих признаков, которые характеризуют все графики (см. рис. 72—74). Это, во — первых, практически одинаковая температура остывания (к моменту действия очередного теплового импульса) точек, расположенных на различной интересующей нас глубине от поверхности а = 2; 5 и 10 мкм, поэтому в даль­нейшем не будем рассматривать градиент температуры остывания, а примем одну среднюю для всех глубин температуру остывания (для а = 5 мкм). Во-вторых, чем больше количество импульсов, тем выше температура остывания, так как интервалы времени от импульса до импульса сокращаются. В-третьих, наблюдается нелиней­ное повышение температуры остывания по длине дуги контакта. При этом в первое время от начала входа в зону контакта это повышение происходит быстро, а затем в оставшееся до выхода из контакта время наблюдается незначительное повышение уровня, особенно для 12 и 20 импульсов.

Почти для всех сталей при 20 импульсах в зоне высо­кой температуры остывания (во второй половине графика по времени) наблюдается чередование подскоков и паде­ний температуры остывания (см. рис. 74). Вероятно, это связано с резким изменением зависимости а, (U) для

е/шл

диапазона температуры, в котором учитывались значе­ния а и q. При этом очень высокая температура приводила к падению < и q оказывался мал в следующем импульсе, что, в свою очередь, значительно снижало температуру остывания и приводило к возрастанию а, и q, а это опять повышало температуру. Вероятно, это связано с дискрет­ностью принятой методики счета. В реальном процессе будет происходить плавное нивелирование, что и на­блюдается на графиках при 8 и 12 импульсах. В связи с этим для 20 импульсов температура остывания бралась по средним значениям между максимальной и минималь­ной температурой остывания.

Рассмотрим в качестве примера один из графиков (например, сталь 40ХНМА с количеством импульсов 12, рис. 75) и определим на нем характерные (интересующие пас) температурные интервалы. Вначале ограничим макси­мально возможные уровни нагревания (пики) температу­рой плавления стали 40ХНМА U„n ^ 1500° С.

В силу допущений, принятых при обосновании одно­мерной схемы теплопередачи, можно измерять время

Рис. 75. Изменение температуры при шлифовании стали 40ХНМА на различной глубине (а) от поверхности за время прохождения уча­стком детали длины дуги контакта (при 12 зернах-импульсах)

в длине пройденного рассматриваемым сечением пути по дуге контакта. Так как одновременно на дуге не может находиться больше двух режущих зерен (даже для п = = 20), то для каждого момента времени можно получить эпюру температуры остывания. Это будет основание (постоянная составляющая) температурного поля на дуге контакта. На эту составляющую накладываются быстро перемещающиеся высокотемпературные пики (темпера­тура под зерном). Постоянная составляющая температур­ного поля определяет механические характеристики ме­талла в зоне шлифования.

Для удобства оценок целесообразно ввести некоторую среднюю температуру по дуге контакта, которая будет определять среднее сопротивление стали пластическому деформированию, характеризующее в конечном итоге

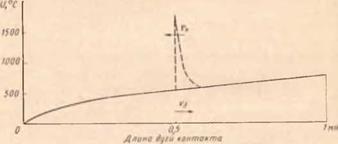
обрабатываемость стали шлифованием. В качестве такой средней температуры принята среднеинтегральная тем­пература остывания. Так, для эпюры на рис. 76 средне­интегральная температура составила 550° С, это — сред­няя температура на дуге контакта для стали 40ХНМА при количестве режущих зерен п = 12.

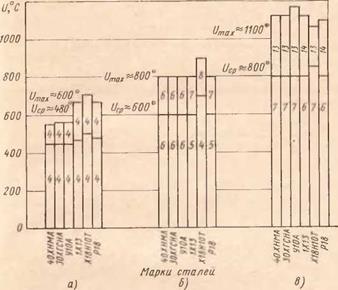
Обработав подобным образом все графики, построим диаграмму средней и максимальной температуры остыва­ния для сталей всех марок и 8, 12 и 20 импульсах (рис. 77). Характерно, что средняя и максимальная температура

Рис. 76. Постоянная составляющая (минимальная температура остывания) температурного поля поверхности детали в зоне шлифования

остывания для сталей всех марок отличается незначи­тельно в связи с тем, что остывание всех металлов проис­ходит от температуры плавления, незначительно отлича­ющейся для сталей всех марок, что позволяет рассматри­вать ее значения только в связи с количеством действу­ющих импульсов — зерен. На каждом столбике выше U(P цифрой обозначено количество импульсов в зоне от U, mt до (Уср, а ниже Uср — количество импульсов, находя­щихся в зоне температуры ниже Ucp

Для оценки температуры металла, в котором рабо­тает абразивное зерно, следует рассмотреть путь зерна круга по различным температурным участкам зоны кон­такта. Абразивное зерно круга входит в контакт с обраба­тываемым металлом, нагретым до температуры 800° С (см. рис. 40 и 41). Таким образом, зерно круга начинает врезание (самый неблагоприятный момент по нагрузке) в наиболее нагретый и легкообрабатываемый металл. Далее в зависимости от количества импульсов проходит ДО Vg (для 8 импульсов) до 2/я (для 20 импульсов) всего 182

мути (равного длине дуги контакта) по металлу, нагре­тому от Umax до / и только оставшуюся часть пути при температуре ниже Uср. При определении интенсивности источника не учитывалось трение боковых поверхностей зерен и трение связки круга о металл, в связи с чем можно считать, что величина £/ср достаточно надежно характе­ризует температурное состояние обрабатываемого металла.

Рис. 77. Средняя температура поверхностного слоя (0,005 мм) в момент прохождения очередного зерна круга дуги контакта для разных сталей и различного количества импульсов-зерен (а — 8; б — 12; в — 20)

Средняя температура остывания для сталей всех марок (рис. 77) для наиболее вероятного количества зерен (успе­вающих поработать на длине дуги контакта) — 8, 12, 20 соответственно составляет 480—500, 550—600 и 800° С.

В некоторых исследованиях [20, 21, 35, 51] темпера­тура в зоне шлифования определялась экспериментально путем шлифования полуискусственных термопар. В связи с определенной инерционностью термопар и несовершен­ством методов тарирования и измерения эта температура отражает некоторые средние значения контактной тем­пературы. Значение этой температуры находится между

Uшах и Uср и ориентировочно подтверждает полученные расчетные значения температуры остывания.

Сравнительные расчеты показывают, что на уровень температуры остывания преобладающее влияние оказы-

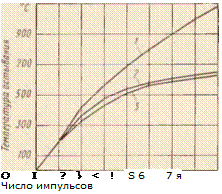Рис. 78. Температура ос­тывания для разного числа импульсов:

/ — линейный расчет при q. К с = const; 2 — расчет с учетом только q (U) 3 — расчет на ЭВМ с учетом <7 (С/), X (£/) и с (£/)

вает зависимость механических характеристик от тем­пературы, т. е. q (U). Зависимости с (U) и ^ (U) сказы­ваются существенно для максимальной температуры (сразу после нагрева), а для температуры остывания лишь в «холодной» зоне, т. е. для первых трех-четырех импуль­сов (табл. 12 и рис. 78).

Таблица 12 Варианты расчета температуры остывания для разного количества импульсов (от 1 до 8) Температура в °С ьарианты расчета У. и, и, V, иь и. V, Линейный расчет («7; X; с = const) 248 423 566 690 801 902 996 1083 Учтено только ят 248 366 475 542 577 606 627 648 Расчет на ЭВМ с учетом Я (to. >■ (U), c(U) 248 327 415 520 567 593 617 640

Поэтому для анализа температуры остывания практи­чески достаточна точность, даваемая приближенной фор­мулой (63), которая с учетом зависимости q (U) прини­мает вид

Следует отметить, что учет изменения теплофизиче­ских характеристик металла методом кусочно-постоянной аппроксимации в формуле (80) неприемлем, так как вслед­ствие больших интервалов времени между работой отдель­ных зерен над одним и тем же сечением поверхности детали колебания температуры очень существенны и не выдерживается условие малости изменения температуры в интервале постоянства Л, и с.

Формула (80) позволяет учесть только наиболее су­щественный фактор для температуры остывания q(U), но ее сравнительная простота позволяет во много раз сократить трудоемкость счета. Это дает возможность использовать ЭВМ малой мощности, а при необходимости выполнять расчеты и без ЭВМ.

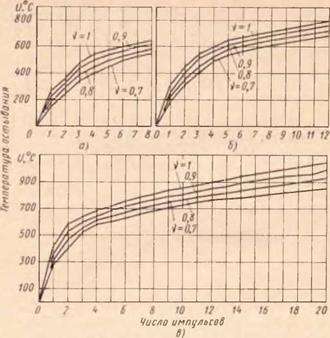
Полученная формула (80) позволяет выявить одну важную особенность температурного поля зоны шлифо­вания. Из формулы видно, что решающим фактором, влияющим на уровень температуры остывания на дуге контакта (см. рис. 78), является средняя скорость убы­вания зависимости q (U), так как пропорциональное уменьшение q (в некоторых пределах) мало сказывается на температуре остывания. Это означает, что температур­ное поле в зоне шлифования слабо зависит от доли тепла, подаваемого в деталь, и, следовательно, устойчиво к изме­нению интенсивности теплового источника. Для иллю­страции этого явления произведем расчет (рис. 79) изме­нения температуры остывания для стали ЗОХГСНА и различного количества импульсов в зависимости от изме­нения коэффициента теплоподвода (v — доля тепла, под­водимого к детали, табл. 13).

Анализ зависимости температуры остывания от коэф­фициента теплопроводности для сталей остальных марок позволил получить приближенную зависимость

(81)

Рис. 79. Изменение температуры остывания в зависимости от изменения доли тепла, отводимого в деталь (v):

а — для восьми импульсов; б — для 12 импульсов; в — для 20 им-
пульсов

Средняя температура остывания для разного
количества импульсов

Таблица 13 Количество тепловых импульсов п Доля тепла, подводимого к детали, V 1,0 0,9 0,8 0,7 Средняя температура остывания (7С1) в °С 8 500 490 462 440 12 595 580 563 550 20 703 685 670 650

іде б(Уср и Лі/—изменение (в процентах) средней тем­пературы остывания и интенсивности источника.

Таким образом, снижение подводимого к детали в зоне резания единичным зерном количества тепла даже на 30% уменьшает среднюю температуру остывания в зоне шли­фования только на 10%.

Слабое влияние интенсивности источника на измене­ние температуры остывания становится понятным, если учесть особенность температурного поля зоны шлифова­ния. Эта особенность заключается в том, что если доля гепла, отводимого в деталь при резании единичным зер­ном, уменьшится, то последующее зерно будет работать в среде более «холодного» и, следовательно, более проч­ного металла, а это приведет к возрастанию общего тепло­выделения и автоматическому повышению температуры металла, срезаемого последующими зернами. Таким обра­зом, сделанное ранее в расчетах допущение о переходе 100%-ного тепла в деталь (сразу после действия источника тепла—зерна) не может существенно повлиять на изменение температуры остывания, определяющей обрабатывае­мость сталей шлифованием.

Примененная в расчете методика «от отдельных импуль­сов (зерен) —■ к общему температурному полю зоны шли­фования», а также учет зависимости теплофизических и механических характеристик сталей от температуры позволили более точно установить характер температур­ного поля детали в зоне шлифования. Особенностью тем­пературного поля зоны шлифования является резкое изменение температуры во времени и по дуге контакта детали с кругом. Очевидно, что для расчета такого поля применение методики, когда в качестве источника тепла принимается условная геометрическая площадь контакта детали с кругом, не отражает реальные колебания темпе­ратуры в зоне шлифования.

Выражение (63) дает возможность оценки любой тем­пературы, а также ее длительности, градиента и зон рас­пространения. При этом расчет учитывает многообразные технологические условия обработки (количество режу­щих зерен, степень их затупления, длина дуги контакта) и может быть использован для решения различных приклад­ных задач.

Таким образом, аналитически решена задача описания температуры в любой точке глубины поверхностного

слоя в любое время (в пределах прохождения зоны кон­такта) с учетом непрерывно меняющейся остаточной тем­пературы, «наследственно» полученной от действия лю­бого количества ранее работавших зерен, что позволило определить температуру срезаемых зернами круга слоев металла.