В работах посвященных теплофизике процессов механической обработки, коэффициент теплопроводности А и теплоемкость с для металла считаются постоянными. В этом случае уравнение теплопроводности (31) линейно и легко решается известными методами математической физики. Отдельные исследователи, учитывая, что теплофизические характеристики металла зависят от температуры, вводят в уравнение их средние значения для исследуемого интервала температуры. Это справедливо только для стационарного процесса. Для нестационарного процесса этот прием дает приемлемую точность лишь в сравнительно узком диапазоне температуры (порядка 200° С для большинства металлов). По данным ряда теоретических и экспериментальных исследований, максимальная температура в зоне шлифования, как уже отмечалось, достигает величин, близких к температуре плавления. Таким образом, имеет смысл оценить степень влияния зависимости теплофизических характеристик металла от температуры на температурное поле зоны шлифования.
Интенсивность источника — зерна q определена ранее через интенсивность напряжений металла в зоне сдвига at-.
Так как ai зависит не только от скорости деформации, но и от температуры деформируемого металла, количество тепла, выделяемого при резании, зависит от температуры срезаемого слоя металла. Следовательно, интенсивность источника q является функцией температуры.
Строгий учет зависимостей A (U), с (U) и q (U) приводит к необходимости решать существенно нелинейное уравнение теплопроводности с внутренней — A (U), с (U) и внешней— q(U), нелинейностями. Для учета влияния этих зависимостей в первом приближении применен метод кусочно-постоянной аппроксимации функций A (U), с (U) и q (U), т. е. непрерывные зависимости заменены кусочнопостоянными (рис. 55). Это позволило воспользоваться линейным решением выражения (53), применяя его к небольшим интервалам времени (рис. 56), за которые температура не успевает сильно измениться, и корректируя каждый раз значения А и с.
Зависимость q (U) используется для определения интенсивности і-го источника в зависимости от температуры, до которой успевает остыть срезаемый металл, нагретый действием предыдущих зерен, к моменту подхода і-го источника — зерна.
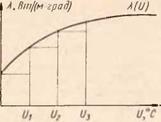При реализации этого алгоритма на ЭВМ оказалось целесообразным несколько видоизменить решение выражения (53). Для реализации внутренней нелинейности введем соответст — Рис. 55. Зависимость теплопро — вующие новые временные водности от температуры интервалы (рис. 56) с учетом
 |
разбивки периода остывания на три равные части. При принятой разбивке в точке с индексом, который делится на четыре, источник начинает действовать, а в точке с индексом на единицу больше заканчивает. Тогда для А-го интервала (с шагом А—пе-
риодом работы импульсов) имеем следующие точки: окончание работы А-го источника
ti = 4^ — з = т + (А— 1) А;
остывание
f/+i=(4ft-3)+i =h[k—-
^+2=<4А-3)+2 = A (А—— jj — j ;
начало работы следующего источника: ti — f 3 =4k ~ hk,
где k — номер источника; h — шаг разбивки точек остывания.
Шаг h вводится потому, что для различного количества импульсов при постоянной дуге контакта он будет меняться.
Обобщая формулы (57) и (58), ввели безразмерный критерий
1=0
Функция П (6) может быть применена и для ручных расчетов, для чего имеет смысл изучить и затабулировать ее.
Новая методика учета в уравнениях теплопроводности ^ непрерывно изменяющейся по времени (остаточной) температуры и реализация этого влияния в безразмерном критерии открывает большие возможности расчета нестационарных иррегулярных тепловых полей, образованных совокупным действием многих подвижных тепловых источников.