Полученное интегральное решение применимо лишь в зоне шлифования (полоса шириной OL, см. рис. 49), так как только в этом случае правомочно допущение о теплоизоляции границы и возможен учет отвода тепла по другим каналам (кроме детали) вследствие изменения интенсивности теплового источника. Вне зоны шлифования теплоотвод в СОЖ и воздух происходит по закону Ньютона, т. е. необходимо ставить вне участка OL краевые условия третьего рода. Тогда будем иметь составную задачу. Применим интегральное решение только при 0 <С у < L, так как для проверки основной гипотезы необходима только температура в зоне шлифования, потому что только эта температура существенна при анализе обрабатываемости материалов шлифованием.
Прежде чем переходить к рассмотрению теплоотвода по направлениям Z и Y, отметим еще раз масштабные соотношения размеров источников тепла (зерен) и глубину поверхностных слоев детали в направлении X. прогрев которых необходимо определить. Размер источника не-
сколько больше круга диаметром /3 = 0,1 мм (так как надо еще учесть зону пластического сдвига), а среднестатистическая толщина среза одним зерном составляет, как было показано, порядка 0,005 мм, т. е. в 20 раз (линейно) меньше.
По отношению к такой толщине источник — зерно будет представлять плоский тепловой источник, по крайней мере, до глубины, соизмеримой с размерами самого источника. А так как в любых сечениях вдоль траектории движения зерна по всей ширине зоны контакта (справа и слева от рассматриваемого источника) действуют аналогичные источники—зерна, лишь сдвинутые на очень
|
II*
Рис. 51. Расчетная схема |
небольшие отрезки времени, большой потери тепла в направлениях Y и Z, можно полагать, не произойдет, так как риски от отдельных зерен по ширине перекрывают друг друга. Некоторая потеря тепла и его нивелирование по направлениям Y и Z будет, но численно ее могут компенсировать трение связки о металл и источники тепловыделения на зерне, которые здесь не учитывались, в частности, боковое трение зерна о металл, трение стружки о зерно и гидравлическое сжатие глубинных слоев.
Таким образом, в зоне контакта (зона ОМРН, см. рис. 48) можно полагать преимущественно одномерное распределение тепла в глубь металла (по крайней мере, до глубины, равной толщине среза), исключая поверхностные (YZ) границы зоны контакта, где отвод тепла будет двумерным. Однако ширина «запретной» зоны по периметру зоны контакта будет небольшой, соизмеримой с толщиной среза (а = 0,005 мм), т. е. с глубиной рассматриваемого нагреваемого слоя.
Таким образом, для решения локальной задачи, касающейся тонких поверхностных слоев детали в зоне
контакта с кругом, целесообразно упростить принятую расчетную схему. Вырежем в полупространстве х ^ О полубесконечный стержень (рис. 51) с осью, перпендикулярной границе полупространства, и весьма малым поперечным сечением. Размеры сечения стержня будем считать существенно меньшими по сравнению с размерами источника — зерна. Исследуем распределение температуры по выделенному стержню.
При сделанных предположениях можно решать одномерную задачу теплопроводности, когда на конце полу — бесконечного стержня в течение некоторого времени действует источник тепла. Промежуток времени действия источника (нагрев) определяется временем прохождения источника — зерна через поперечное сечение стержня.
Рис. 52. Схема интенсивности источников и их действия во времени
На рис. 51 показана графическая расчетная схема с учетом многократного действия источников. Схема действия источников во времени может быть получена (рис. 52) из схемы для плоской задачи (см. рис. 49) как сечение ее любой прямой (в любой точке длины линии контакта), например А А, параллельной оси Т. Таким образом, след источника в виде параллелограмма выродился в линейные отрезки оси Т.
![]()
Интенсивность источника может быть задана функцией
Так как одномерная задача получается из плоской опусканием пространственной координаты у, можно сразу получить для нее интегральное решение. Функция Грина для полубесконечного стержня с вторым краевым условием имеет вид
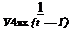
![]()
G(x, t, х’, f) =
Учитывая выражение (47) по аналогии с решением па стр. 150, сразу получим
и(^і) = и0 + ^{-тШ=ге~^п dt’. (481 Ф.) 1 4 л ч (/ — t )
0
В этом случае интегрирование практически ведется по всем интервалам (Г,-; Тt + т) с отличной от нуля интенсивностью источников, лежащим левее точки Ґ = t (см. рис. 52).
Учитывая проведенное выше осреднение интенсивности источника, можем положить q (t) = q = const.
В этом случае интеграл в решении уравнения (48) может быть выражен через специальные функции.
Рассмотрим интервал времени 0 < t <С т. Для этого интервала интегральное решение уравнения (48) примет
ВИД
| ІЛІ
Функции in erfc x изучены и затабулированы. Таблица первых шести функций приведена в работе [23]. В сочетании с таблицами выражение (53) вполне пригодно для инженерных расчетов и позволяет строить температурное поле детали в зоне шлифования как результат совокупного действия зерен-источников с учетом их движения по дуге контакта.
Для анализа обрабатываемости сталей шлифованием наиболее существенна температура остывания; это температура, до которой успеет остыть металл в рассматриваемом сечении (нагретый действием предыдущих зерен) к моменту подхода очередного зерна.
Принимая, что зерна на круге расположены равномерно, получим Ть = ІТ (см. рис. 52); Tt — время входа в рассматриваемое сечение і + 1 зерна. Температура металла в этот момент и определяет его теплофизическое и механическое состояние. Из выражения (53) можно получить формулу, определяющую температуру остывания в зависимости от номера (пі) последнего прошедшего через сечение источника. Для этого вычислим значение U (х, t) для t = тТ:
1
рии процесса.
Применение безразмерных критериев позволяет установить общие зависимости для различных условий шлифования, не обращаясь к конкретным числам. Рассмотрим изменение этих критериев для различных количеств действующих зерен-источников на глубинах, необходимых для оценки обрабатываемости (табл. 9).
под оператором суммирования в ряд Тейлора в окрестности (а = 0, 6 = 0) и ограничиваясь в силу быстрой сходимости получающегося ряда двумя первыми членами разложения, получим с учетом выражения (58):
где m = 1, 2, . .п.
Погрешность формулы (59) для сформулированных выше условий не превышает 1,5%. Формула (59) позволяет без построения всего температурного поля сразу находить интересующую нас температуру остывания.
При интегрировании для упрощения было сделано допущение, что q (t) = q = const, т. e. была усреднена 156
|
Изменение температуры от интенсивности и длительности действия источника
|
|
t/ (остывание kt = 100т)
|
интенсивность источника. Но из рис. 44 видно, что зависимость q (t) имеет большие колебания около ее среднего значения. Простота полученных решений (53) и (59) позволяет оценить эффект усреднения интенсивности источника. Так как зависимость q (і) кусочно-постоянна, интеграл для нее вычисляется по формулам (53) и (59), которые содержат только больше слагаемых. Для упрощения оценок отбросим в q (t) постоянную составляющую и рассмотрим различие температурных полей от двух источников (рис. 53).
Суммарные количества тепла, выделяемого этими источниками, примерно одинаково;
= 10<7-0,1т = qi Q2 = qr.
Соотношение времен т и 0,1т и интенсивностей q и 10<7 примерно соответствует пропорциям на эпюре интенсивностей (см. рис. 44). При оценке температуры остывания учтем, что время остывания в условиях шлифования составляет примерно 100т. Расчет по формулам (51) и (59) максимальной температуры прогрева и температуры остывания дает соотношения, приведенные в табл. 10.
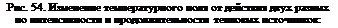
 Изменение температурного поля на шлифуемой поверхности от действия тепловых импульсов разной интенсивности и длительности приведено на рис. 54.
Изменение температурного поля на шлифуемой поверхности от действия тепловых импульсов разной интенсивности и длительности приведено на рис. 54.
Как видно, изменения интенсивностей источников затронули только высокотемпературную зону, занимаю-
100 т
/ — от пластической деформации; 2 — от трения
щую не более 3% общего поля. Существенная для оценки обрабатываемости температура остывания, как следует из графика и табл. Ю, практически не изменилась (особенно для глубинных слоев *>0). Таким образом, для оценки температуры остывания осреднение интенсивности источника практически не влияет на рассчитываемую температуру остывания.
Дальнейший анализ высокотемпературной зоны показывает, что максимальная температура даже усредненного по интенсивности тепловыделения источника оказывается выше температуры плавления стали. Для оценки максимальной температуры необходимо учитывать, кроме переменной интенсивности источника, возможность фазовых превращений в металле, т. е. ставить задачу Стефана.