Расчетная тепловая схема и анализ. температурного поля поверхности детали. в зоне шлифования

Среднестатистические модели схем взаимодействия шлифовального круга с деталью (см. рис. 40 и 41), выпол­ненные с соблюдением относительного масштаба в размерах зерен их углублений в металл, длины зоны контакта и прочих размеров, положены в основу геометрических очертаний теплосодержащего слоя детали в зоне контакта ее с кругом. Из этих схем следует, что в процессе шлифо­вания каждый элементарный участок поверхности детали (соизмеримый с шириной риски от одного зерна) от мо­мента входа в зону контакта с кругом до момента выхода из нее испытывает действие ряда тепловых импульсов, являющихся результатом воздействия отдельных зерен круга. Ниже предпринята попытка аналитически описать
температурное поле поверхности детали в зоне контакта (в пространстве и времени), являющееся результатом совместного воздействия отдельных подвижных источни­ков — зерен.

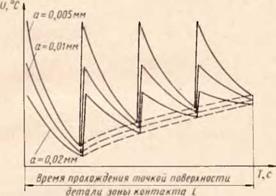
Целью расчета является построение графиков в коор­динатах температура U — время Т по типу приведенных на рис. 45 для различных условий шлифования. По оси абсцисс графика откладывается время, за которое эле-

Рис. 45. Предполагаемый характер изменения тем­пературы поверхности детали (на разной глубине а) за время Т прохождения точкой поверхности зоны контакта

ментарный участок поверхности проходит длину зоны контакта. За это время элементарный участок поверхности детали подвергается действию тепловых импульсов — зерен, количество которых может колебаться в значи­тельных пределах в зависимости от технологических усло­вий шлифования (зернистости круга, диаметров детали и круга). На рис. 45 в качестве примера приведен предпо­лагаемый плоский график U—Т для условных четырех тепловых импульсов. Одно семейство кривых иллюстри­рует изменение температуры слоев детали, расположен­ных на разной глубине от ее поверхности, а второе семейство кривых (штриховая линия) проходит через точки наименьшей температуры, до которой успевает остыть тот или иной слой к моменту подхода очередного теплового импульса.

Последнее семейство кривых дает искомую темпера­туру, определяющую механические свойства металла в мо­мент его резания.

Из масштабных схем взаимодействия круга с деталью (см. рис. 40 и 41) видно, что кривизна детали в пределах длины зоны контакта несущественно влияет на геометри­ческую схему взаимодействия круга с деталью, поэтому

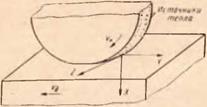Рис. 46. Объемная схема
взаимодействия круга с де-
талью

для составления расчетной схемы можно допустить, что деталь представляет собой полупространство (рис. 46). В процессе шлифования зона действия источников (дуга контакта) передвигается по поверхности детали со ско­ростью уд, а сами источники — зерна перемещаются вдоль дуги контакта со скоростью ук. Пренебрегая кри­визной круга в зоне контакта и изменением интенсивности источников в зависимости от положения на дуге контакта, можно принять в качестве исходной тепловой схемы модель, приведенную на рис. 47. Введем систему коор­динат. Ось X направим в полупространство перпенди­кулярно его границе, ось У— по границе вдоль вектора скорости (v осьZ—по границе полупространства перпендикулярно и.

В уравнении (31) полагается, что теплофизические характеристики материала не зависят не только от тем­пературы, но и от координат, т. е. материал изотро­пен, не учитываются структура материала и возможная его теплофизическая неоднородность. Для материала использованы усредненные значения теплофизических характеристик.

Регулируя отвод тепла в стружку, в зерна круга, в СОЖ путем изменения интенсивности теплового источ­ника, можно принять границу полупространства теплоизо­лированной.

При сделанных допущениях задача о распределении температуры детали в зоне шлифования математически формулируется следующим образом:

источник тепла расположен на границе полупространства при х — 0).

Описание работы источников и решение задачи можно представить геометрической схемой. Уравнение (31) опре­деляет функцию U (х, у, z, і) как функцию точки четырех­мерного пространства XYZT (Т — координата времени). Тогда действие источников происходит в гиперплоскости YZT, уравнение которой х — 0. Можно описать действие источников в гиперплоскости YZT геометрически при помощи некоторых трехмерных форм. Прежде чем строить геометрические аналоги в координатах YZT, рассмотрим частный случай, более простой и наглядный для плоской задачи, для сечения Z = 0 (рис. 47). Начало координат выбираем так, чтобы в момент t 0 круг начал входить в контакт с рассматриваемым участком поверхности де­тали OL, равным длине зоны контакта АВ — L (точка В относится к кругу, а О — к детали; при t = 0 они совпа­дают).

В такой постановке задачи функцию U (х, у, t) можно рассматривать как функцию точки трехмерного простран­ства XYT, а действие источников проходит в плоскости

YT. Построим геометрическую схему действия источни­ков в плоскости YT. Точками А и В обозначим концы зоны контакта. Примем, что зона контакта перемещается вдоль границы детали со скоростью ид. Поэтому закон движения начала зоны контакта (точка В) и конца (точка А) составит

У в = V;

Ya = vJ— L-

L

войдет в контакт и начнется выход его из зоны контакта,

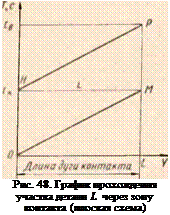который закончится в мо­мент ів — 2 tK. Графически это движение в координатах YT изображено на рис. 48. ОтО до /к участок 0L входит в зону контакта и в момент /к совпадает с ней (НМ = L), а далее начинает выходить (сокращаясь по линии HP) и заканчивает выход в точке Р в момент времени /„ = 2tK.

Рассмотрим схему дейст­вия тепловых источников

зерен на рассматриваемый участок поверхности детали 0L (см. рис. 47), для чего изобразим на круге ряд ис-

Таким образом, каждый источник оставляет на услов­ной плоскости YT графика (рис. 49) след (во времени) в виде заштрихованного параллелограмма.

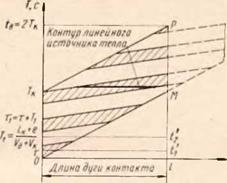Рис. 49. График прохож­дения участка детали L через зону контакта с действием ряда тепловых импульсов (плоская схе,- ма)

Уравнение процесса для рассматриваемой плоской схемы (z = 0) получится из уравнения (36) опусканием переменной г:

Интегрирование во втором интеграле практически ведется по заштрихованным областям (см. рис. 49), рас­положенным ниже прямой = t, соответствующей интересующему нас моменту времени t.

Если положить условие ф (я, у) = U0 = const, что вполне реально, то первый интеграл в уравнении (46) существенно упрощается. Непосредственные вычисления показывают что

+ е

Таким образом, при вполне реальном начальном усло­вии Uо = const интегральное решение задачи (39)—(41) имеет вид

V (х, у, 0 =

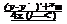
я (<Л п

4лх (t — С)

£ Di

где Dt — — заштрихованные области, лежащие ниже пря­мой ti = t (см. рис. 49).

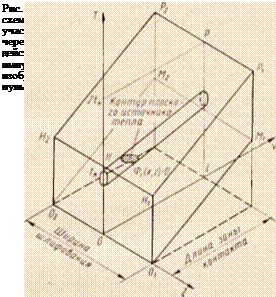
Полученное решение можно обобщить для расчетной объемной схемы на случай пространственной задачи тепло­проводности, описываемой уравнением (31). Плоская схема действия источников (во времени и одном направле­нии пространства У) становится трехмерной, так как добавляется координата Z (по ширине источника — зерна и всей ширине шлифования). Параллелограммы на рис. 49 превращаются в цилиндры (рис. 50), направляющими ко­торых являются контуры источников — зеренФ, (z, х) = 0, а образующими — прямые, параллельные прямой:

) У = (Од + »к) U z = 0.

Эти цилиндры, являющиеся следами во времени кон­туров плоских YZ источников —зерен, заполняют парал­лелепипед ОjO.#j. M,Л4 гРгР2 (для длины L зоны кон­такта) в соответствии с частотой расположения зерен на круге (в плоскости YZ) и временем вступления зерен в ра­боту друг за другом (по координате Т). На рис. 50 условно показан один источник и его след. В общем случае эти цилиндры-следы заключены между плоскостями

у = 0; у = L; у = vRt у = vj — L0.

Интенсивность источника для объемной схемы распре­делится так:

q (у, z, t) (внутри цилиндров); О (вне их).

Для полупространства функция Грина имеет вид

где Df — область действия і-го источника — зерна в системе YZT, ограниченная поверхностью Ф(. (у, г) = 0.

Интегрирование ведется с учетом ряда источников тепла, попавших в рассматриваемую зону. Если интере­сующая нас точка с координатами (х, у, z, t) попадает внутрь цилиндра (см. рис. 50), т. е. в зону действия тепло­вого источника р0 (у, z, t), то происходит нагревание и температура повышается; если точка оказывается вне действия источника и р (у, z, t) 0, то происходит про­цесс остывания.