Работа пластического деформирования. и трения в срезаемом слое и расчет интенсивности. тепловых источников — зерен круга

Прежде чем перейти к составлению расчетной тепловой схемы и формулированию начальных и краевых условий задачи, установим интенсивность теплового источника — абразивного зерна — путем анализа работы пластиче­ского деформирования и трения в срезаемом слое; эта величина существенно влияет на точность определения температуры тела. При пластическом деформировании металлов обычно принимается, что затраченная работа внешних сил равна сумме работ сжатия и сдвига, трения и диспергирования поверхности обрабатываемой детали.

Рассмотрим вначале в общем виде эти составляющие баланса энергии. Силы сжатия, сдвига и трения подчи­няются законам пластического деформирования и отно­сятся к категории массовых сил, действующих в объеме деформирования. Кроме массовой и поверхностной силы, связанной с диспергированием, т. е. образованием новых поверхностей, в скоростных процессах деформирования определенную роль играют инерционные силы. Так как в деформируемом теле под действием внешних сил отдель­ные точки его приходят в движение, выведем вначале общее уравнение движения.

Внутри тела малой поверхностью dS выделим эле­ментарный объем dV. Рассмотрим системы действующих

па этот объем сил [1 ]. Поверхностная сила p„dS, массо — >

вая сила р/7 и сила инерции pwdV действуют на объем dV, который движется с ускорением w. Распространяя дей­ствие сил на все деформируемое тело, получим три силы:

Таким образом, работа деформирования расходуется на увеличение кинетической энергии отдельных точек тела в процессе деформации и на собственно деформирова­ние тела. Та часть работы, которая идет на сообщение ки­нетической энергии тела, характеризуется скоростной функцией L, а работа деформации — функцией диссипа­ции энергии Е.

Скоростное деформирование имеет свои особенности, которые обусловливают существенные различия в про­цессе деформирования металлов. С увеличением ско­рости деформации возрастает сопротивление пластиче­ской деформации. Повышение механических свойств зависит от конечной скорости распространения дислока­ций внутри кристалла [1]. При скоростном деформиро­вании дислокация не успевает выходить на поверхность границы зерна. Особенно сильно это влияние проявляется на горячей обработке металлов, когда скорость переме­щения дислокаций значительно снижается. В этом случае оказывается весьма существенной (как уже указывалось ранее) зависимость интенсивности напряжений от скорости и температуры:

Oi = f(v, U).

При скоростном деформировании, кроме изменения сопротивления металла пластической деформации, су­щественную роль начинают играть инерционные силы.

Возникающие инерционные силы изменяют поля скоро­стей, скорости деформаций, деформации, напряжения перераспределяют работу деформирования по объему металла. Особенностью скоростного деформирования является возможность образования и распространения волн в металлах. Однако эти явления находятся в настоя­щее время в стадии начального исследования.

Многими исследованиями установлено, что деформи­рование при высоких скоростях приводит к локализации области пластических деформаций. Особенность в этом случае заключается в том, что накопленная при скорост­ном деформировании кинетическая энергия переходит в месте ее образования в работу деформирования. При этом пластическая деформация локализуется в области максимума накоплений кинетической энергии [1] и вы­полняется условие

Li —|— Е —— (Т^Є^ .

Тогда формула (35) запишется следующим образом: А = [ | j | olei dV dt.

‘(О (Г)"

Вычислить это выражение трудно вследствие слож­ности экспериментального определения сколько-нибудь точных значений объема деформируемой зоны V и интен­сивности скорости деформации є,-. Кроме того, неизвестен закон распределения напряжений в зоне сдвига и в зоне трения. Поэтому рассмотрим работу деформирования и трения, выраженную в конечных величинах сил и пере­мещений применительно к принятой расчетной форме абразивного зерна.

На рис. 42 дана схема резания одним зерном круга и зоны контакта зерна с металлом, по которым возникают составляющие сил Pt :PZs—сила от сопротивления металла сдвигу по поверхности сдвига Ss Р, —сила трения по

2тр

вершине зерна (площадке /3), по поверхности 5В и Р „ —

2тр

сила трения по боковым поверхностям зерна S6.

Тогда

а интенсивность теплового источника зерна соответственно 136

составит (если считать, что вся работа переходит в тепло) Я V» “Ь? тр Ру К’

В отношении распределения тепла между металлом, зерном и охлаждающей средой имеются различные точки зрения. Так в работе [51 ] принято, что в металл переходит 80% тепла, в работе [59] — 81—46%, а в работе [50] —

Рис. 42. Зоны контакта зерна с металлом

100%. Нам представляется, что тепловой баланс сильно изменяется во времени. С течением времени большая часть тепла забирается с поверхности детали охлаждающей средой (жидкостью и воздухом). Однако в момент реза­ния и в течение очень короткого промежутка времени до прихода следующего зерна в зоне контакта основная масса (близкая к 100%) идет на нагрев металла, так как подвод охлаждающей среды в зону контакта затруднен, а теплопроводность металлов в десятки раз больше тепло­проводности электрокорунда и СОЖ-

Учитывая, что тепловыделение рассматривается в мо­мент действия источника — зерна и далее в течение очень короткого времени до подхода следующего зерна, при­
нимаем, что в эти периоды времени почти все тепло пе­реходит в деталь.

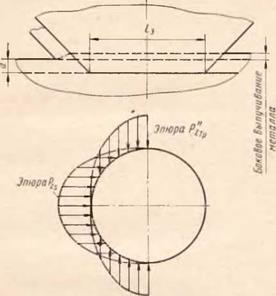
На рис. 43 даны схемы поверхностей, по которым происходит тепловыделение. По поверхности 5S (половины усеченного конуса с образующей О’А) действует сила Рг, по поверхности 5б (половины усеченного конуса

с образующей O’N) действует сила Р » и по поверхности

, *ТР

5В (круга радиуса 00’ = — j-) действует сила Р ■ , т. е.

п _ l/~aj25 cos ft с •’i sin Pi ‘

Р • = 0,5prs5B; Р • = 0,5рт55б.

тр *Ч>

Так как требуется определить нагрев глубинных слоев металла, расположенных перпендикулярно к обработан-

Рис. 43. Схемы поверх­ностей тепловыделения

ной поверхности, принимаем условно поверхность дей­ствия источника, через которую подается тепло, совпадаю­щей с обработанной поверхностью, т. е. в виде плоского источника тепла с контурами полуокружностей радиусов О К и 00".

Выше были определены силы P2i и Р ‘ . Остается неиз-

гтр

вестной сила бокового трения Р « .Из схемы видно, что

гтр

тепловыделение от этой силы происходит в направлении нормали к образующей конуса O’N, направленного под углом 45° к горизонтальной плоскости, принятой за пло­скость действия источника. Следовательно, в глубинные слои обработанной поверхности может перейти только часть общего тепла от силы бокового трения Р « . На осно­вании этого тепловыделение от бокового трения металла о зерно в дальнейших расчетах не учитывается.

Для определения удельной интенсивности источника каждая сила относится к площади, на которой она дей­ствует:

V325cos Р

о. =————— й—

sin р 1 к>

9тР = 0,5|тт5ук = 0,5-0,3tsuk = 0,15tsuk.

Сопоставление величин qs и qTp показывает, что qTP составляет только 4% от qs-

Эти силы действуют на разных участках источника: qs — по поверхности полукольца с радиусами ОК и О’О,

a qTр—по площади окружности радиуса 0’0 = ~-.

На рис. 44 приведена эпюра интенсивности источника по

осевому сечению зерна. Так как qs и <7тр действуют на разных участках, для удоб­ства расчетов усредним интен­сивность qs и qrр по всей площади их действия. Тогда

Qs =

Qtp — ^тр^в — Рис. 44. Эпюра интенсивности

„ г, источника тепла по осевому

Поверхность с>5 находим, сечению зерна

исходя из следующих сооб­ражений. Для определения силы Рг& необходимо собрать по поверхности конуса О’А (см. рис. 43) проекции эле­ментарных сил на направление скорости (см. рис. 42) и

отнести их к площадке шириной О’А = . и длиной /,

sin рj

(диаметр зерна). Тогда без учета уширения зерна от ко-

е в/,

">’са Ss~Smfr-

Пренебрегая наклоном этой площадки к горизонталь­ной плоскости = 22°), будем считать, что весь тепловой поток, нормальный к О’А, переходит в глубинные слои поверхности детали. При /3 = 0,1 мм, а = 0,005 мм, pt = 22° Ss = 0,00133 мм2, a Qs = 4 0,00133ок. т, 0,00532 скт,.

Соответственно,

лі’

Sn = -4- = 0,0079 мм2;

QTp = 0,15-0,0079укт5 = 0,001 18укт5.

Тепловыделение, вызванное трением зерна (с площад­кой /3 = 0,1 мм) о металл, составляет только 20% от тепловыделения пластического деформирования, хотя с ростом площадки /3 количество тепла от трения будет увеличиваться:

Q = Qs + Qjp = 0,0065yKTs. при 5 = 5s + 5„

__ Q [0,0065ukts

Qcp — Яо — -^- — 0,00133 + 0,079

С учетом ts = y*= имеем q0 0,41

Это значение принято в качестве расчетной средней величины интенсивности плоского источника тепла, макси­мальные размеры которого по длине (в осевом сечении зерна) составляют (как это видно из расчета площадей

5s и 5„) —|- /3. Значение q0 учитывает тепловыделе­

ние от пластического сдвига в зоне максимальных каса­тельных напряжений и трения по вершине зерна и не учитывает трение стружки по поверхностям зерна, боко­вого трения зерен о металл и некоторого тепловыделения в зоне гидростатического сжатия.