Силы сопротивления пластическому. деформированию и трению при шлифовании

Единой методики определения аналитическим путем действующих сил резания пока нет. Это связано главным образом со сложностью картины пластического течения деформируемого металла при резании, наличием наряду

со сдвигом одновременно действующих напряжений сжа­тия и влиянием сил трения. Одновременный учет этих факторов (сдвига, сжатия и трения), значительно меня­ющихся с изменением многообразных условий процесса резания, весьма затруднен. Обычно при рассмотрении сил резания делаются допущения, в результате которых пренебрегают теми или иными составляющими; чаще пренебрегают силами трения по задней грани инструмента.

В общем случае при определении равнодействующей силы резания следует исходить из равновесия ряда актив­ных (внешних) и реактивных (внутренних) сил, действу­ющих на режущий инструмент. К этим силам относятся: сила сдвига (от т5), действующая в направлении плоскости сдвига (Pj), сила сжатия (в направлении нормальных напряжений а), сила трения стружки по передней грани и сила трения обработанного металла о заднюю грань инструмента. Обычно каждую из этих составляющих определяют отдельно, исходя из условий, имеющих место в точке ее приложения. Так, сила сдвига рассматривается обычно как образующаяся только от действия максималь­ных напряжений сдвига в направлении плоскости сдвига (без учета нормальных напряжений), а сила трения по задней грани определяется из условий задачи статиче­ского упругого вдавливания. Так как эмпирическое опре­деление силы трения отдельно от других сил очень за­труднено, а при аналитическом исследовании факторов, влияющих на эту силу, допускается определенный про­извольный выбор коэффициента трения, то ее определение в разных работах производится по-разному. Так, в одних работах сила трения на задней грани инструмента связы­вается с силами, действующими на передней грани, в дру­гих отвергается такая связь.

Для правильного определения составляющих сил ре­зания большое значение имеет распределение напряжений в примыкающей к срезу области. Рассмотренные выше напряжения были связаны с пластическими деформа­циями. Однако в объемах, прилегающих к пластически деформируемой зоне и не имеющих свободных поверхно­стей для перехода напряжений в пластические деформа­ции, возникают большие напряжения гидростатического давления (всестороннего сжатия), не вызывающие зна­чительных пластических деформаций (закон неизменяе­мости объемов) и постепенно переходящих (с удалением от очага их образования) в упругие напряжения и дефор — 72

мации, также уменьшающиеся с удалением от места пла­стической деформации.

Определим составляющие сил резания Р. и Ру (на 1 мм ширины среза) с учетом трения обрабатываемого металла по передней и задней поверхностям зерна, осно­вываясь на эпюре распределения напряжений, построен­ной вдоль контактных поверхностей инструмента и обра­батываемого металла с использованием нормальных и касательных напряжений по характерным направлениям, полученным ранее.

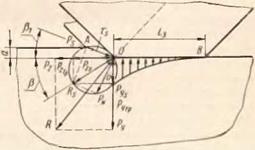На рис. 29 дана схема резания стружки одним зерном круга, построенная для следующих технологических уело-

вий обработки: толщина среза а = 0,005 мм (характерная для средних подач чистового шлифования), угол при вер­шине зерна 90°, передний угол зерна у = —45°, усадка стружки і] 1,35, Pj = 22°, площадка затупления зерна /3 =0,1 мм, соответствующая среднему состоянию за- тупленности зерен электрокорунда, образующаяся через 5—10 мин работы круга. Наличие значительных площадок затупления зерен и отрицательный передний угол [17, 29] объясняют весьма большое и устойчивое отношение

Р,

резании металлическим инструментом

Очень малая толщина среза и стружки при значитель­ных размерах самого зерна дает возможность отметить некоторые особенности (рис. 29): малая толщина среза обеспечивает более полное соответствие условиям пло­ского деформированного состояния; при малой толщине среза можно считать все силы приложенными к режущей

кромке (точке О), причем эти силы могут быть приведены к одной равнодействующей, так как моменты сил незна­чительны.

Используя известные свойства кругов Мора о геометри­ческом суммировании касательных и нормальных напря­жений 161 ] и помещая точку пересечения вектора каса­тельных и нормальных напряжений вначале координат (см. рис. 29), построим эпюру распределения напряжений, полагая, что размер напряженных зон различен в разных местах контура.

Используя соотношение —— = 1,5 [формулы (21) и

Тс

(23)], где о и т5 — средние напряжения по всей напря­женной зоне, построим эпюру распределения напряжений от верхней границы зоны сдвига (условно линии ОА) до конца площадки трения точки О. Круг Мора между направлениями t, и а дает распределение напряжений, возникших в результате пластического течения металла в зоне линии ОА, причем наличие нормальных напряже­ний является обязательным условием, подготавливающим и обеспечивающим сдвиг в направлении О А. Именно дей­ствие, с одной стороны, передней поверхности инструмента, а с другой — действие сил от нормальных напряжений (ниже линии О А) обеспечивают пластическое течение металла в направлении ОА. При этом напряжения сдвига ts и потребное для сдвига нормальное напряжение о я» 1,5ts определяются свойствами металла (ts f (аг)), а напряженная зона — длиной линии ОА (следовательно, а и Pj). При этом положение линии О А (угол Pj) уже учи­тывает трение стружки по передней грани, так как угол рх определен экспериментально по усадке стружки шлифо­вания, на величине которой уже сказалась сила трения стружки по передней грани [17, 61 ].

Если бы вершина зерна была абсолютно острой, то можно было бы не учитывать упругие деформации и тре­ние по задней грани вследствие небольшой площадки трения и определить равнодействующую сил резания R по этим напряжениям. Однако при значительных площад­ках трения, характерных для абразивного зерна круга, по этим площадкам возможен контакт с металлом на зна­чительном протяжении, который поддерживается упру­гими напряжениями и деформациями, охватывающими область гидростатического сжатия, что можно обосновать следующими предположениями. Возникшие при пласти — 74

ческой деформации нормальные напряжения направлены перпендикулярно линии сдвига ОА и охватывают область между этой линией и контуром круга Мора. Несмотря на незначительные деформации этой зоны, соизмеримые по величине и характеру с упругими деформациями сжатия (вследствие отсутствия пластического течения металла в каком-либо направлении), нормальные напряжения могут быть весьма большими.

Теоретически за все время перемещения площадки зерна ОВ при условии ее плотного прилегания к обраба­тываемому металлу не возникает условий для резкого снятия нормальных напряжений. Кроме того, учитывая тенденцию образования встречного «заборного конуса» и радиуса на площадке трения в результате износа зерна в точке О, можно ожидать дополнительного сжатия ме­талла под площадкой трения, по крайней мере, в первой ее половине.

Однако в реальном процессе следует учитывать, что неровности площадки трения зерна 1641 будут произ­водить пластическое смятие и частичное диспергирование трущейся поверхности металла, причем контакт между ними будет из непрерывного в зоне точки О переходить во все более прерывистый по мере удаления от точки О, а также, учитывая высокую контактную температуру площадок трения, можно ориентировочно предполагать закон убывания нормальных напряжений по длине пло­щадки трения от наибольших в точке О до нуля в точке В. Закон распределения напряжения вдоль /, неизвестен, однако, учитывая изложенное выше, примем криволиней-

ныи закон убывания, при котором аср — у, где а0 ‘7

я» а « 1 ,5ts — напряжение на участке под точкой О.

Силы (рис. 29), вызывающие распределение напря­жения (которые являются реакцией на приложенные извне силы), можно классифицировать следующим об­разом: Р, — тангенциальная составляющая равнодей­

ствующей силы резания R, состоящая из суммы двух сил — P*s — тангенциальной силы от напряжений пластического сдвига (с учетом трения стружки о переднюю грань и нормальных напряжений) и Pzтр — тангенциальной силы от трения металла о заднюю грань; Ру — радиальная составляющая равнодействующей силы резания R (или радиальная сила), которая возникает как реакция ме-

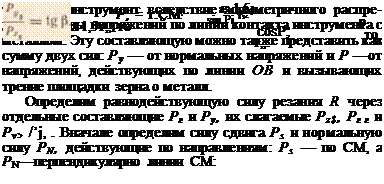Соотношение этих сил определим следующим образом:

Найдем величину Ру, уравновешивающую напряже­ния вдоль линии ОВ, полагая, как указывалось выше, что и напряжения п зона их распределения уменьшаются от режущей кромки (точка О) до конца линии контакта (точка В). Принимая, что напряжение а0 в точке О будет приблизительно равно а и, следовательно, а„ = а = = 1,5ts. Затем определим среднее напряжение по всей длине площадки трения (/3 = ОВ):

_ о„ _ 1 ,5ts «Р 3 3 *

Тогда

При шлифовании абразивные зерна круга переме­щаются в пластически деформируемом металле. Допустим, что поверхность касания каждого зерна состоит из боль­шой совокупности дискретных площадок, на которых коэффициент трения [.і не изменяется по длине линии кон­такта, т. е.

%«И% = 0,5ц/л.

Соотношение сил Ри и Рг составит — —.

“тр ‘тр И и

‘тр

Суммарные тангенциальные и радиальные составля­ющие найдем из выражений

Таким образом, по линии контакта абразивного зерна с металлом действуют напряжения сдвига и сжатия, которые зависят от прочности материала при скоростях и температуре деформации шлифованием а(., а их распре­деление является характерным для двух процессов ре­зания (сдвиг и сжатие) и трения. Эти процессы определяют и две автономные системы сил, действующие на зерно. Одна система зависит от толщины среза а, а вторая — от величины площадки затупления /, задней поверхности зерна. Связь между этими системами сил осуществляется

критических тангенциальных напряжений т5, при которых происходит сдвиг и стружкообразование, движением ин­струмента и рабочей силой создается нормальное напря­жение о 1,5ts. Это напряжение распространяется по убывающему закону на площадку трения зерна о металл. Следовательно, силы резания и трения зависят от вели­чины и, кроме того, силы резания зависят от толщины среза а, а силы трения — от величины площадки /, и коэффициента трения.