Расчет напряжений при шлифовании

Процесс резания металлов является процессом конеч­ных (больших) пластических деформаций, претерпевае­мых не всем телом в целом, а только его частью (очагом ’ігформации). В этом случае принимается гипотеза жестко — пластического тела и делается допущение, что в зоне пчага деформации упругими слагаемыми деформации, как малыми по сравнению с остаточными, можно пре — псорсчь.

Решение системы трехмерных уравнений (11) в част­ных производных в общем случае, как уже отмечалось, і іпгіаію с большими трудностями. Поэтому обычно объем­ную задачу упрощают до плоской задачи течения, при

.. і ■ л tlVr ‘Ні/ п

кптрои I, = 0 и 0 тождественно. Си-

| ісма уравнений (11) преобразуется следующим обра — ’1 Корчак 49

При плоском течении шестое уравнение из системы уравнений (13) примет вид

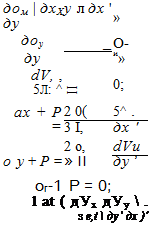= — Р

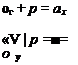Следовательно,

откуда

Тогда первое и второе уравнения равновесия из си­стемы уравнений (13) принимают вид

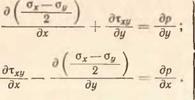(14)

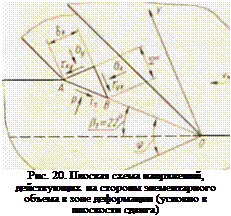Условия равновесия элементарного объема металла мри плоском резании для шлифования могут быть пред — | і а плены следующей схемой (рис. 20). Установлено, что

плоскость сдвига для принятых условий шлифования располагается под углом 22° к направлению век-

юра скорости резания. Направление этого угла опре — /мміястся законом наименьшего сопротивления, который и применении к пластической деформации [44] разрабо — |пн Г. Треска еще в 1865 г. С. И. Губкин формулирует «он’ закон следующим образом: в случае возможности їм рсмсщсния точек деформируемого тела в различных направлениях каждая точка деформируемого тела пере — 4* 51

мещается в направлении наименьшего сопротивления. Угол сдвига при любых условиях обработки устанав­ливается, как указывает К. А. Зворыкин, такой, при котором расход энергии будет минимальным или (при постоянной скорости резания) будет минимальной сила резания. Из теории пластичности известно, что плоскости сдвига являются траекторией максимальных по абсолют­ной величине касательных напряжений, а материальные волокна наибольшего удлинения и наибольшего укороче­ния взаимно перпендикулярны и в любой стадии деформа­ции располагаются под углом 45° к направлению сдвига. Это положение справедливо при стружкообразовании для объемов металла, близко расположенных к свободной поверхности, поэтому точку А условно расположим на свободной поверхности.

Рассмотрим условия равновесия элементарного объема, ограниченного двумя гранями, перпендикулярными оси 0Z, и треугольным контуром со стороной АВ, рас­положенным таким образом, что максимальные каса­тельные напряжения т5 совпадают с плоскостью сдвига. Тогда по линии ВБ (параллельной оси OY) будет про­исходить наибольшее удлинение элементарного объема, а по линии АБ (параллельной оси ОХ) — наибольшее укорочение. Это построение относится к весьма малому объему металла, подвергающемуся начальной деформации в области нижней границы плоскости сдвига (к разовому «элементарному» сдвигу). Непрерывное скольжение эле­ментов относительно друг друга является сложной немо­нотонной деформацией сдвига совместно с сжатием и на­личием трения по передней грани, что ориентирует тек­стуру всей стружки (подсчитанную по большим конечным деформациям) под углом р2 = 30е, который является рядом бесконечно большого числа элементарных сдвигов и не совпадает вследствие сложности и немонотонности процесса деформации с направлением ВБ (OY). Обычно угол 45° проявляется в текстуре стружки только у сво­бодной поверхности стружки [17].

При плоском течении а + р 0 и напряжение о„ (пог), нормальное к площадкам элементарного объема, лежащим в плоскости чертежа, равно р. Условие равно­весия можно записать в виде проекций сил, действующих на элементарный объем [57] в направлении р

Тогда

Таким образом, нормальное напряжение по формуле (23) найдено для точки А, исходя из граничных условий па свободной поверхности, в силу которых линия ОА непосредственно перед выходом на свободную поверх­ность изгибается и образует с ней угол так как вдоль

свободной поверхности действуют сжимающие напряже­ния, вызывающие сдвиг.

Отношение нормального напряжения к касательному можно определить из формул (21) и (23):

Максимальное давление pwax можно получить исходя щ условия, что ртах будет в точке, где задняя поверх­ность переходит в переднюю. В этой точке должно удов­летворяться условие пластичности и, следовательно, ртах должно быть связано с сопротивлением обрабатываемого материала сдвигу в условиях резания, т. е. с величи­ной тсдв. Так, Н. Н. Зорев, основываясь на исследова­ниях М. М. Саверина по контактной прочности материа­лов, выводит следующее уравнение:

тсдв = — Щ — (°-25 + F2) Ртах-

В этом уравнении при р = 0,5 следует, что тгдв «э

I >5ршах-

В работах В. Палмера и П. Окслея на основании тео­рии пластичности дается следующее выражение для нормального напряжения в точке выхода линии сдвига нн свободную поверхность:

^ = l+ 2(-f-P,)v

11ри рх = 22°*=»-^- напряжения составят ол = рА — 1,8т..

Нормальное напряжение у режущей кромки опре­делится из выражения

°а = Ро = °Л +Т*1П ("§■)•

где RA и R0— соответственно расстояния от свободной поверхности и режущей кромки до центра веера линий скольжения.

Если Ra >■ R0, то о0 > аА, следовательно, гидро­статическое давление у режущей кромки больше, чем у свободной поверхности.

Одни исследователи считают, что касательные напря­жения распределяются равномерно вдоль плоскости сдвига, а нормальные напряжения изменяются вдоль плоскости сдвига, достигая наибольшего значения у сво­бодной поверхности (точка А, рис. 20) и уменьшаясь к вершине резца. Другие исследователи утверждают, что и те и другие напряжения убывают с увеличением рас­стояния от точки О, где они максимальны. Большинство исследователей считает, что касательные напряжения мало или совсем не изменяются вдоль плоскости сдвига, а по изменениям нормальных напряжений высказываются диаметрально противоположные мнения. Более правиль­ным представляется точка зрения ряда исследователей [1, 17] о возрастании гидростатического давления от свободной поверхности (где одно из значений главного нормального напряжения равно нулю) к режущей кромке (наблюдается более сложное напряженное состояние, чем у свободной поверхности). Однако, так как задача на­стоящего анализа сводится к определению сравнительного сопротивления разных сталей пластическому деформиро­ванию шлифованием, а не определению характера распре­деления самих напряжений в зоне деформации, полу­ченные выражения (21) и (23) могут быть взяты за основу как приближенные и средние (по плоскости сдвига) напряжения.

Таким образом, установлена приближенная функцио­нальная связь касательных и нормальных напряжений с интенсивностью напряжений ог Определив о, = / (е, е, eit U0 для сталей и сплавов различных марок, можно определить напряжения и силы сопротивления деформи-1 рованию, создаваемые сталями и сплавами различных марок при шлифовании.

В большинстве работ, рассматривающих сложные тех­нологические процессы пластического течения (ковка, прокатка, резание), делаются попытки аналитического определения напряжений на основе данных стандартных механических испытаний образцов.

Сопоставление зависимости напряжений от деформа­ции при резании и при стандартных механических испы — | и и иях материалов представляет интерес по ряду при­нц и: во-первых, имея эти зависимости при самом простом ипде испытания (растяжении или сжатии), можно в ка — коїі-то мере предсказать поведение этого материала при обработке резанием и, во-вторых, определив зависимость о( к( при резании, можно судить о поведении материала при таких больших скоростях деформации, которые не­достижимы при существующих методах механических испытаний материалов. Механические испытания мате­риалов в исходном состоянии проще, чем испытания резанием.

Работы, в которых производятся подобные сопостав­ления, имеют большое научное и прикладное значение. Например, А. М. Розенберг и А. Н. Еремин [52] пред­ложили рассчитывать силы резания, предварительно опре­делив сопротивление сдвигу в зоне деформации по твер­дости стружки. В работах Н. Н. Зорева предлагаются более рациональные методы расчета сил резания по ме­ханическим свойствам обрабатываемых материалов в ис­ходном состоянии. Сопоставляя напряжения при пласти­ческом сжатии или растяжении и резании металлическим инструментом, почти все исследователи обычно приходят к выводу, что эти напряжения вполне сопоставимы при эквивалентных деформациях, хотя скорости и темпера­тура деформации существенно отличаются.

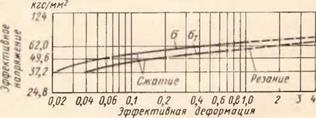
Так, на рис. 21 приведены данные, полученные С. Ко — башпи и Е. Томсеном, по сопоставлению напряжений сжатия и резания, из которых видно хорошее совпадение кривых, свидетельствующих о возможности приближен­ного экстраполирования напряжений сжатия до соответ — ‘ піующих деформаций резания (хотя при высоких сте­пенях деформации резанием напряжения от сжатия кор­ректируются незначительно). Аналогичные сравнения вы­полнены в работе М. О. Недельмана, а на растяжение — в работе Н. Финни, где также получены приближенные совпадения между резанием и механическими испыта­ниями на растяжение.

Влияние температурного и скоростного фактора де­формации в процессе резания взаимно уравновешивается и позволяет производить приближенное сопоставление напряжений при скоростном резании и статическом растя­жении или сжатии, хотя такое сопоставление строго теоретически и методически неверно. Иногда такое сов-

Рис. 21. Сопоставление напряжений в зоне’стружкообра — зования с кривыми упрочнения, полученными при стати­ческих испытаниях на сжатие [17]

падение сил при статическом испытании материалов и при резании является чисто внешним, так как в формулы сил (или напряжений) резания входят эмпирические коэф­фициенты (постоянные), которые учитывают поправку на напряжения от скорости деформации резанием.

Процесс шлифования характеризуется еще более вы­сокими скоростями деформации и температурой, чем резание металлов, при которых предугадать совместное (хотя в определенной мере и компенсирующее) влияние этих факторов на изменение статических напряжений оказывается невозможно, так как влияние скорости де­формации при высокой температуре более значительно, чем при низкой.

Функциональная связь о, с е,., г, и U° может быть установлена экспериментально путем лабораторных испы­таний на сжатие или растяжение с последующей графи­ческой и аналитической обработкой данных путем аппрок­симации некоторыми аналитическими выражениями. Вос­

пользуемся для решения этой задачи методикой Г. А. Смирнова-Аляева и В. М. Розенберг.

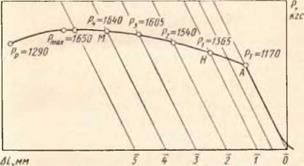
Вначале рассмотрим связь а,- = / (є,), которая может быть получена по данным испытаний на простое растяже­ние. Диаграмма испытания на разрыв образцов из стали показана на рис. 22. Специальные графические построе­ния на диаграмме исключают упругие деформации и дают позможность получить таблицу значений, зависящих друг от друга (растягивающей силы Р и абсолютных остаточных удлинений А/ образца). Отношение растя-

J ♦ J Р і о Рис. 22. Машинная диаграмма испытания образца стали на разрыв

і ивающей силы Р к площади сечения образца характе­ризует напряжения, возникающие в испытуемом об­разце а, а отношение абсолютного остаточного удлинения к расчетной длине образца — степень деформации є. Однако как площадь поперечного сечения образца, так н его длина в процессе пластического растяжения изме­няются, поэтому понятия о напряжениях и степени де­формации могут получать различный смысл.

Конкретизацией понятий о напряжениях и степени деформации при простом растяжении образцов занима­лись многие исследователи, которые предложили ряд формулировок и методов обработки результатов испы — Iпнпй [57].

Один из вариантов заключается в построении диа — | рнммы зависимости эффективного напряжения (о =у~, іде Г о—исходная площадь сечения образца) от отно-

сительного остаточного удлинения образца —. Но

‘о

последнее характеризует стадию процесса растяжения до образования шейки. Поэтому второй вариант заключается в построении диаграммы зависимости «истинного» напря-

Р

жения о, = -у (где F — текущая площадь сечения)

от относительного уменьшения площади сечения об — F0 — F

разца —У-г,— = б!.

Г п

Для определения степени деформации для любых схем напряженного состояния следует использовать обоб­щенные показатели напряженного состояния (интенсив­ность напряженного состояния)

В устойчивой (равномерной) фазе растяжения образца в поперечном его сечении действуют равномерно распре­деленные по сечению осевые растягивающие напряже­ния or2 = 0j, сга = сз = 0. откуда о, = о, Однако в фазе растяжения, соответствующей процессу локализации де­формации в центральной части шейки, неизбежно появ­ляются тангенциальные и радиальные напряжения, по­этому среднее по сечению значение интенсивности напря­женного состояния ст, должно быть несколько меньше среднего по сечению растягивающего напряжения ctj =]

= Юпред = — у> Т. е. Ст, = — til (сг)пред. где 11 !< 1. Зна­чение поправочного коэффициента ц, зависит от отноше­ния —г—. (где Fv— площадь сечения к моменту начала

образования шейки, /— площадь шейки после раз — F

рыва), а не от ——. При этом диаграмму интенсивности

‘о

напряженного состояния предлагается строить в за­висимости от є,-: Єі = 1п-^?-.

Значения -=- и а для двух произвольных точек г о

диаграммы (см. рис. 22), например Н и М, устанавливаем по восходящей ветви опытной кривой (точки предела текучести, истинного предела прочности и момента раз­рушения знаем по диаграмме).

Показателем задаемся и в случае необходимости корректируем его (для черных металлов N і «25, для цветных N± 10). Константы С, С, и (сг()пред опре­деляются расчетным путем. Так, учитывая, что для точки разрушения в пределах практической точности послед­ний член равен нулю, получаем выражение константы С, решая следующую систему уравнений:

где FH, FM и Fm — площади сечения образца в точках Н, М и в точке, соответствующей моменту образования шейки.

Решая эту систему уравнений относительно кон­станты С, после преобразований получаем расчетную формулу

Значение константы (н^пред. представляющей собой предельное значение напряжений, соответствующих весьма большой степени деформации, можно получить из фор­мулы

(а,)пред = а1 раз + С ~~ . (25)

1 о

Значение коэффициента С в выражении (24) находим и і условия

| С, — [(а,)1фел —— о,„ | ’ .

Определение координат точек диаграммы а,—е(. произ­водится по формулам [57]:

_ Р /„ + — V

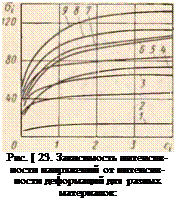
В качестве примера на рис. 23 приведен для различ­ных материалов график зависимостей ст( от ег, выраженных

через аппроксимирован­ные кривые.

Таким образом, анали — тически-экспери менталь­ным способом можно уста­новить зависимости о(—♦>, для сталей разных марок при различной темпера­туре испытания. При г, = = 2-ь2,5 и более а. прак­тически остается постоян­ной для различных мате­риалов (рис. 23). Интенсив­ность напряжений прак­тически не возрастает с ростом интенсивности де­формации при больших конечных степенях дефор­мации. Аналогично в дру­гих работах отмечается, что, когда вся пластическая деформация или значитель­ная ее часть проходит в узкой зоне, напряжение практи­чески не зависит от степени деформации. Рассчитанная ранее для условий шлифования степень деформации

сдвига составила є = 4,72, а еі — ^ = 2,8, т. е. весьма

большую величину, лежащую на горизонтальном участке линии сгг—е(. (рис. 23) в области больших пластических деформаций. Эю дает возможность принять максималь­ную интенсивность напряжений, вычисленную по испыта­ниям на разрыв с учетом весьма большой степени дефор­мации, в качестве критического напряжения разруше­ния, соответствующего максимальным касательным напряжениям, при которых происходит сдвиг в зоне дефор-

мацни при шлифовании, т. е.

_ __ (<ті)прід

5 ~ К З

При выводе формулы (26) не принималось во внимание действие гидростатического давления р в зоне сдвига при резании. Гидростатическое давление характеризует фи­зическое состояние рассматриваемой частицы и является, как и интенсивность напряженного состояния, инвари­антной величиной (т. е. не зависит от выбора координат­ных осей).

Большое гидростатическое давление может оказать существенное влияние на разрушающие напряжения. Однако при небольшом гидростатическом давлении его влиянием на интенсивность напряжений можно прене­бречь. По данным работы [39], гидростатическое давле­ние при резании сталей разных марок (при U = 20° С) порядка 60—120 кгс/мм2. В дальнейшем принимаем, что среднее вдоль линии сдвига гидростатическое давле­ние изменяется для сталей разных марок пропорцио­нально изменению (аг) по ранее полученной фор­муле [23]

„ _ (°і)прецп

P~~WT’

т. е. р примерно в 1,5 раза больше т5.

Кроме оценки влияния гидростатического давления, необходимо также учесть влияние температурно-скорост­ного режима деформации. Подразумевается, что темпе­ратурно-скоростные факторы должны быть учтены диа­граммой о(-—е(. и, таким образом, найдут свое отражение н численном выражении р и т5. Рассмотрим вначале неко­торые теоретические положения и принятую методику учета температуры и скорости деформации при использо­вании в расчетах результатов испытания разных сталей на разрыв.

Влияние температуры и скорости деформации на ин­тенсивность напряжений таковы, что они не могут рассма — гриваться отдельно, так как один из факторов е£ способ­ствует увеличению, а другой (11°) — уменьшению ап и какой из факторов будет преобладать, зависит от соче­тания абсолютных значений е(. и U° для стали каждой марки. При этом характер функции ст,—с. при низкой тем-

пературе (до температуры рекристаллизации), когда не происходит разупрочнения, будет отличаться от харак­тера ее при высокой температуре (выше температуры рекристаллизации), когда наблюдается полное разупроч­нение. Последнее происходит во времени и этот механизм окажет влияние на ог, если скорость деформации ег окажется меньше скорости процесса рекристаллизации.

Сложный характер взаимного влияния U0 и е(. на вели­чину at обусловил тот факт, что в теории пластичности рассматриваются изотермические процессы деформации.

При одном характере влияния температуры деформации на о; (в сторону ее уменьшения) причины появления вы­сокой температуры различны. В большинстве работ вы­сокая температура деформируемого тела принята за фак­тор среды (нагрев внешними источниками). В работе [24] высокая температура рассматривается как результат ра­боты деформирования при больших скоростях деформа­ции, когда тепло локализуется в местах ее образования, в связи с чем наблюдается адиабатический процесс. По­следний характеризуется уменьшением а(. (по сравнению с изотермическим процессом статической деформации, характерным для низких скоростей), особенно для низко­температуропроводных жаропрочных и титановых спла­вов. При этом скорость резания действует как фактор, определяющий время деформации, с уменьшением кото­рого стг возрастает вследствие того, что процессы разупроч­нения (отдыха и рекристаллизации) реализуются в мень­шей степени.

В то же время с ростом скорости резания и, следова­тельно, скорости деформации в зоне сдвига повышается температура, приводящая к снижению о(- (по сравнению со статическими испытаниями). Однако количественная оценка влияния температуры па сг(- при адиабатической деформации еще недостаточно разработана, поэтому ниже учитывается только более сильное влияние внешней вы­сокой температуры (как среды нагретого металла) на величину что встречается при шлифовании (т. е. зерна работают в среде металла, нагретого ранее работав­шими зернами).

Рассмотрим экспериментальные данные по влиянию U° и е(. на а;.

Данные испытаний, полученных на стали У10 160], приведены на рис. 24. Левая часть графика представляет

собой температурную зависимость истинного (одноосного) сопротивления деформации (для схемы сжатия и степени деформации 20%), составленную для разных скоростей деформации. Правая часть графика выражает зависимость напряжения от скорости деформации при разной темпе­ратуре. При температуре выше 300—400° С напряжения резко падают, особенно для низких скоростей деформа — кгс/ммг

0 200 Ш 600 800 1000U,°С510~* 5-Ю 3 5 W’1 5Ю’с, с ‘

а) 6)

пип, кроме того, с ростом скорости деформации сопротив­ление деформации значительно увеличивается, особенно для высокой температуры (от нескольких до десяти раз).

‘ ледователыю, скорость деформации наряду с температу­рнії должна обязательно учитываться при оценке сопро — 1 пиления сталей пластическому деформированию в ско­ростных и высокотемпературных технологических про­цессах.

15 работе [60] на основе анализа большого статисти­ческого материала (для сталей и сплавов 120 различных мирок при различных степенях деформаций) получены некоторые общие закономерности изменения напряжений
от скорости деформации, которые могут быть положены в основу методики исследования влияния скорости де­формации при испытании разрывом (соответствие этих закономерностей сжатия разрывным испытаниям дока­зано специальными экспериментами).

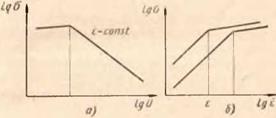
Зависимости а—U° и а—є (рис. 25) для разных сталей в общем виде могут быть представлены следующим обра­зом. При повышении температуры до 300—400° С (рис. 25, а) изменяются средние амплитуды и частота колебаний атомных частиц и средние (равновесные) расстояния между частицами (тепловое расширение). При этой температуре и очень малых скоростях деформации у большинства ста­лей наблюдается незначительное повышение напряжений вследствие деформационного и теплового старения. Для температуры выше 300—400° С кривая а—U° резко опу­скается вниз и ее наклон обусловлен температурой и ско­ростью рекристаллизации. У ферритных, углеродистых и легированных конструкционных сталей кривые а—U° наиболее крутые, а у аустенитных и карбидных сталей — пологие; среднее положение занимают стали с мартен­ситной структурой 160]. Известно, что у аустенитных сталей рекристаллизация протекает при температуре выше 1200° С и с небольшой скоростью, в то время как у ферритных сталей она осуществляется уже при тем­пературе 800—900° С.

Обратимся теперь к графику а—є (рис. 25, б). Сочетания различной температуры и разных скоростей деформаций дают перегиб кривой в зависимости о—е. Участки до и после перегиба соответствуют за — и дорекри — сталлизационным условиям деформации. Положение вза — имоперехода этих участков по шкале скоростей соответ­ствует критической скорости деформации ет, характер­ной для каждой температуры. При этом с увеличением температуры U > U увеличивается критическая ско­рость деформации ет, так как с увеличением скорости де­формации уменьшается время на рекристаллизацию, и она успевает произойти только при более высокой тем­пературе.

Для технически чистых металлов влияние времени нагружения є связано с тепловыми флуктуациями. Вслед­ствие тепловых колебаний атомных частиц поле сил вза­имодействия между ними испытывает флуктуации. В ре­зультате некоторые из необратимых сдвигов в зернах 66

образца возникают до того, как в процессе нагружения среднее по времени поле напряжений для соответствующих плоскостей скольжения достигает критической (разру­шающей) величины. Вероятность возникновения доста­точно значительной флуктуации внутренних сил за данный промежуток времени с уменьшением его при прочих рав­ных условиях также уменьшается. Поэтому с переходом к более высоким скоростям нагружения относительная доля термодиффузионных сдвигов уменьшается и, сле­довательно, сопротивление пластической деформации уве­личивается.

Рис. 25. Характерные изменения напряжений с ростом температуры (а) и скорости деформации (б) для размой температуры деформации V i U2

Для сплавов с метастабильной структурой (например, закаленных сталей) картина влияния скорости нагруже­ния и температуры оказывается более сложной вслед­ствие старения — рекристаллизации, т. е. повышения со­противления пластической деформации со временем в ре­зультате изменения состава термодинамически неравно­весного твердого раствора.

Таким образом, на участке кривой а—є до е. т (рис. 25, б) время нагружения соизмеримо с временем, необходимым на частичные тепловые флуктуации и частичную ре­кристаллизацию, т. е. деформации происходят в за — рекристаллизационной зоне, а с увеличением скорости нагружения выше », (и снижением времени нагружения) тепловые флуктуации внутренних сил и процессы рекри­сталлизации не успевают оказать заметного влияния на а, и необратимые сдвиги в металле образца имеют в основ­ном атермический характер, мало зависящий от скорости деформации (наклон линии меньше), а процесс скоростной
деформации приближается по характеру к «холодной» статической деформации *.

Таким образом, зависимость о—є [60] может быть раз­бита на две части: первую до ет — область «горячего» деформирования, где lg сг = /і, lg є, и вторую после ет — область «холодного» атермического деформирова­ния, где влияние температуры (даже довольно высокой) не успевает проявиться в полной мере вследствие малого времени деформирования (lg а = п2 lg ё).

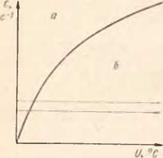Рис. 26. Общий характер измене-
ния критической скорости деформа
ции єт от температуры [10]:

а — атермическая дорекристаллиза-
ционная область; б — зарекристал-
лизационная область

Критическая скорость деформации гт для разной тем­пературы является одним из важнейших показателей, определяющих величину и характер изменения сопротив­ления деформации аг

Зависимость г, от температуры приведена на рис. 26.

При общепринятых статических лабораторных испы­таниях образцов для разной температуры деформации скорость нагружения (деформации) примерно одна и та же (параллельные линии на рис. 26).

С увеличением скорости деформации даже при высокой температуре процесс может оказаться в дорекристаллиза — ционной атермической области, где влияние є на а менее значительно (пологая прямая lg а = пг lg є на рис. 25, б) по сравнению с зарекристаллизационной областью де­формации. Использование данных лабораторных стати-

1 При чрезмерно высоких скоростях нагружения возрастают силы инерции, которые в этом случае не учитываются, и влияние времени на увеличение о должно начать расти снова вследствие развития вол­новых явлений.

ческих испытаний образцов, полученных при разной тем­пературе деформации, но без учета скорости деформации, характерной для исследуемого технологического про­цесса, приводит к существенным ошибкам. Поэтому ниже приведены некоторые теоретические положения и экспе­риментальные данные, которые позволяют учесть влияние скорости деформации и скорректировать соответству­ющим образом данные статических лабораторных испыта­ний образцов разных сталей.

По данным работы [60], различие температурно­скоростной зависимости (см. рис. 25) сопротивления де­формации у разных сталей обусловлено (не считая, есте­ственно, влияния различных абсолютных величин напря­жений) главным образом не величинами л, и п2 (танген­сами углов наклона прямых в координатах lg о—lg є), которые сохраняют близкие значения для сталей и спла­вов разного химического состава, а критической скоростью деформации вт, характеризующей переход от «холодной» деформации к «горячей».

Эта критическая скорость деформации ет для разных сталей и разной температуры деформирования оказывается в зависимости от гомологической температуры, характер­ной для разных сталей. Гомологическая температура для

каждого металла вычисляется как отношение 0 = — f**-,

v ЛЛ

где £/деф — температура, при которой происходит дефор­мирование металла в °К, U„n — температура плавления в °К. Гомологическая температура для разных сталей может быть вычислена по линии солидус диаграммы со­стояния железо—карбид железа с учетом влияния па температуру плавления различных элементов.

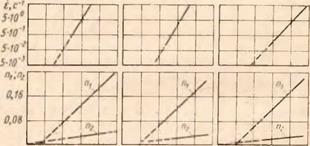
На рис. 27, а, б, в приведены зависимости между ет и показателями п1 и я2 для сталей различных групп. При 0 < 0,3 каждому значению ет соответствуют два значения пх и пг; это означает, что при этой температуре график а—в имеет два участка: до — и зарекристаллиза — ционный с точкой взаимоперехода по ет. Если скорость деформации не достигнет ет, то зависимость а—в выпол­няется только в виде крутого зарекристаллизационного участка с показателем пх. Из графиков можно получить зависимость

(27) 69

Значения коэффициентов а и b для сталей разных групп приведены в работе 1601.

Рассмотрим общую методику построения графиков а(.—є по результатам лабораторных испытаний на разрыв образцов разных сталей при разной температуре деформи­рования. Зависимость ст—е; в логарифмических коорди­натах выражается, как это показано выше, прямой с точ­кой перегиба при ет. Так как абсолютные значения на-

0 0,2 ОМ 0,6 0,8 В 0 0,2 ОМ 0.6 0.8 9 0 0.2 ОМ 0,6 0,8 в а) 6) 8) Рис. 27. Зависимость критической скорости деформации от гомологической температуры 0 [60]:

а — углеродистые стали; б — аустенитные стали; в — карбидные

стали

пряжений для стали каждой марки различны, а характер изменения этих напряжений в зависимости от темпера­туры и скорости деформации изменяется по примерно одинаковым законам, то для каждой группы сталей (аусте­нитных, карбидных, ферритных) можно построить гра­фики а,—е,., используя величины nt и tin (рис. 27) и опре­деляя ет по формуле (27) для каждой гомологической тем­пературы.

Построение графиков (рис. 28) для стали каждой марки производится следующим образом. Имеются зна­чения (сг^пред — подсчитанные по результатам статических испытаний на разрыв |> 10” 3 с-1) сталей разных

марок. Испытания на деформацию этих сталей произво­дились при различной температуре. В результате испы­таний получены значения (о()пред.

w

Для сталей соответствующей группы, к которой ОТНО­СИТСЯ исследуемая сталь, берутся значения коэффици­ентов п1 и п2, а для соответствующей гомологической

температуры 0 = , которая подсчитывается по фор-

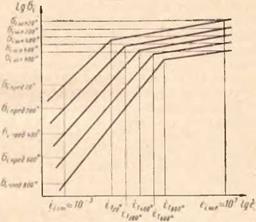муле (27), соответственно определяется критическая ско­рость рекристаллизации рт (рис. 27). Отложив абсциссы

и проведя через них соответствующие ординаты, строим прямые через точки <7(ПКД—е(ст под углом наклона a" (tg ос^ ■ Пх), соответствующие каждой температуре до пересечения с ординатами ет. Из точек пересечения проводим прямые под углом наклона ‘< (л^ = tga^), соответствующим каждой температуре. Получаем график изменения интенсивности напряжений (о()пред в зави­симости от температуры и скорости деформации для стали данной марки.