ВЗАИМОСВЯЗЬ ПРОИЗВОДИТЕЛЬНОСТИ ШЛИФОВАНИЯ. СТАЛЕЙ С ИНТЕНСИВНОСТЬЮ НАПРЯЖЕНИЙ

Сложная пластическая деформация металлов, харак­терная для большинства технологических процессов формо­изменения (прокатки, давления, резания), вызывает не­обходимость вначале проанализировать механику про­цесса резания с учетом особенностей шлифования для возможности последующего использования данных стан­дартных механических испытаний разных сталей (напри­мер, на разрыв или сжатие) для оценки их обрабатывае­мости шлифованием. При этом не ставится цель совер­

шенствования ранее разработанных моделей пластического течения металлов при резании, а только изменения их к условиям шлифования (т. е. с учетом специфической геометрии инструмента-зерна, высокой скорости дефор­мирования, высокой температуры).

О существенном влиянии скорости и температуры деформации на величину напряжений изложено в работе [60], где указано, что напряжения при статических стандартных испытаниях образцов (на разрыв или сжатие) при комнатной температуре могут значительно отличаться от напряжений, возникающих в том же металле при от­личных скоростях деформации и высокой температуре, причем как в сторону увеличения напряжений (с ростом скорости), так и в сторону их уменьшения (с ростом температуры). Таким образом, без анализа механизма пластического деформирования, характерного для шли­фования, и особенно без учета температурно-скоростного фактора деформации невозможно рассчитать сопротивле­ние деформированию сталей в процессе шлифования и, следовательно, правильно оценить производительность их обработки.

Анализ напряженно-деформированного состояния обычно сводится к установлению закономерных связей (с определенными допущениями) между геометрической стороной течения (деформации, их скорости) и механиче­ской (напряжения, силы). При разных условиях и ре­жимах воздействия различные материалы проявляют индивидуальный, только им присущий характер связи напряжений с деформациями. При современном уровне раз­вития пластической механики точное математическое реше­ние этой задачи для реальных металлов и технологичес­ких процессов деформирования вообще недостижимо [57].

Некоторые частные решения течения металлов в реаль­ных процессах могут быть получены только в результате принятия большего или меньшего числа упрощающих и. схематизирующих процесс допущений. Обычно пласти­чески деформируемым металлам приписывают ряд упро­щающих свойств: однородность, равномерность смещения материальных элементов в отдельных искусственно выде­ленных частях, равномерность напряженного поля в огра­ниченных объемах, идеальную упругость или пластич­ность. Критерием приемлемости того или иного допуще­ния должны служить, во-первых, отсутствие противоре — 30

чип течения идеализированного процесса с законами механики и, во-вторых, приемлемая для практики^сте­пени расхождений результатов расчета с данными про­верочного эксперимента.

І Ісходя из основной теоретической гипотезы настоя­щего исследования о том, что в процессе шлифования абразивные зерна круга выполняют работу резания и среде металла, нагретого до высокой температуры действием предыдущих зерен, можно предположить, что пбрабатываемый металл в большей мере приближается и идеально пластичному состоянию, чем холодные (20° С) металлы, хотя и для них делают такое допущение при расчете. В теории пластического немонотонного течения для больших конечных деформаций и идеально пластич­ного металла принимаются следующие основные положе­ния: в рассматриваемой частице тела направления глав­ных осей напряженного состояния совпадают с направле­ниями главных осей скоростей деформаций (или направ­ляющего тензора напряжений с направляющим тензором скоростей деформаций); объем частицы в процессе пла — . тпческой деформации не меняется (закон [постоянства объема или несжимаемости); интенсивность напряженного состояния (ос) остается постоянной по всему объему деформируемого тела.

В математической и прикладной теориях пластичности гипотеза совпадения главных осей напряжений и скоро­тиш деформаций принимается как один из главнейших принципов, который может быть положен в основу рас­четов при решении практических задач. Следовательно, иля правильной оценки сопротивления деформации необ­ходимо установить функциональную связь между напря­жениями и скоростями деформации с учетом температуры деформации.

Для общей характеристики напряженно-деформиро — и. итого состояния тела при немонотонных больших пластических формоизменениях применяются две обоб­щающие характеристики: е( — интенсивность скоростей деформаций и of — интенсивность напряжений. Связь между ними может быть установлена [1] из анализа работы (энергии) деформирования элементарного объ­ема dW:

После соответствующих преобразований получаем в тензорном виде

откуда следует, что Da = Di, t на основании чего форму­лируется основной физический закон в области больших пластических деформаций: направление действия алгеб­раически наибольшего главного напряжения всегда сов­падает с направлением наиболее быстрого удлинения ма­териального волокна, а направление алгебраически наи­меньшего главного напряжения с направлением наиболее быстрого укорочения.

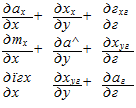В общем случае анализ напряженного состояния тела в окрестностях любой его материальной точки сводится к интегрированию системы дифференциальных уравнений в частных производных, которую можно составить, ис­пользуя уравнения равновесия, а также подвергнув преобразованиям уравнения, полученные выше, и запи­сав их в дифференциальной форме для произвольного расположения координатных осей:

Эта система уравнений в теории пластичности назы­вается системой уравнений течения идеально-пластиче- 1 кого вещества. В тех случаях, когда сгг по условиям нщачи нельзя считать постоянной величиной по всему пГи. ему формоизменяемого тела, в систему (11) вводят искомую переменную сг(-.

Необходимость математической постановки задач, по условиям которых значение о, нельзя принимать постоян­ным, возникает в случаях, когда деформируемый металл обладает деформационным упрочнением (т. е. деформация производится при температуре ниже точек рекристалли — інцііи) и когда высокие скорости деформации способствуют упрочнению и при температуре выше температуры рекри — | галлизации (т. е., несмотря на высокую температуру, рекристаллизация не успевает происходить в полной Мере).

При этих условиях общая постановка задачи пласти­ческого течения относится к задачам современной мате­матической теории пластичности [57]. Интенсивность напряжений для различных металлов и условий деформа­ций находится в сложной функциональной зависимости главным образом от интенсивности деформаций, интен­сивности скоростей деформаций и температуры:

at = f(eltet, in. (12)

Эту функцию в практических расчетах обычно уста­навливают с определенными допущениями опытным путем для каждого металла по результатам его испытания на растяжение или сжатие [57]. Таким образом, несколько упрощающих постановку задачи допущений, схематизи­рующих рассматриваемый сложный процесс пластиче­ского формоизменения, позволяют ценою отклонений 01 истинной картины его протекания описать задачу мате­матически.

Рассмотрим дальше ряд положений, которые позво­ляют решить расчетно-эпирическим путем задачу пласти­ческого течения металла при шлифовании. Для определе­ния сил и работы пластического деформирования необ­ходимо определить напряжения (в общем случае а;) для высоких скоростей деформации (в общем случае е(), характерных для шлифования. Таким образом, общая задача сводится к определению экспериментально-расчет­ным путем интесивности деформаций є,- и интенсивности скоростей деформаций характерных для шлифования; расчетно-эмпирическому установлению связи между на­пряжениями, деформациями и скоростями деформации в температурно-скоростном интервале, характерном для процесса шлифования сталей разных марок.