Задача минимизации погрешностей формообразования при бесцентровых методах абразивной обработки в общем случае учитывает множество факторов и включает целый ряд подзадач со своими критериями. Поэтому она должна решаться на основе многокритериальной оптимизации.
Существенный вклад в процесс формообразования при бесцентровом шлифовании и суперфинишировании вносят три группы факторов: геометрические, кинематические и силовые. Проведенные исследования установили, что все они взаимосвязаны и требуют одновременного рассмотрения, как при проектировании станков, так и при их наладке и подналадке в процессе эксплуатации. Кинематические и силовые параметры во многом являются производными от геометрических параметров, поэтому предлагается минимизировать геометрические погрешности, а кинематические и силовые параметры использовать в качестве ограничений. Такой подход при формировании единого критерия геометрической точности позволяет перейти от многокритериальной к многопараметрической оптимизации.
При бесцентровом шлифовании и суперфинишировании обрабатывают детали в виде тел вращения, и геометрическая точность складывается из точности направляющей, которая формируется траекторией движения заготовки, и точности образующей (окружности), которая определяется погрешностями микробазирования при вращении. При этом от точности направляющей зависит как форма номинальной поверхности, так и отклонения продольного сечения, а точность образующей влияет на отклонение от круглости, огранку и волнистость.
Формообразующая траектория при обработке с продольной подачей создается основными базирующими элементами станка — ведущим кругом и опорным ножом при шлифовании и двумя валками при суперфинишировании. Расчет этих элементов на основе теории огибающих в пространстве позволяет получить необходимую траекторию относительно абразивного инструмента. Ведущий круг или валок представляют собой тела вращения со сложным осевым профилем или с нелинейчатой винтовой поверхностью. В первом случае ведущий круг выполняют абразивным, а во втором — металлическим. На традиционных бесцентровых шлифовальных станках без многокоординатной системы ЧПУ требуется также решение задачи правки абразивных ведущих кругов.
При бесцентровом суперфинишировании цилиндрических и бомби- нированных поверхностей целесообразно использовать одну и ту же пару валков для обработки деталей различных размеров. Для этого выполняют подналадку станка по межосевому расстоянию и углу перекрещивания осей валков. Теоретической основой для оптимизации наладки служит разработанная математическая модель для расчета пространственной формообразующей траектории. Метод подналадок имеет ряд ограничений, например, при достижении малых радиусов бомбины детали. Проведенные эксперименты выявили диапазон применимости данного метода с учетом различных ограничений.
Кинематические и силовые факторы играют важную роль, особенно при бесцентровом суперфинишировании, когда осуществляется силовое замыкание контакта. Из уравнений равновесия получены инвариантные условия стабильного вращения заготовки, не зависящие от силы резания. Установлено, что правильный выбор углов контакта в большинстве случаев обеспечивает устойчивость процесса по силовым параметрам. Анализ кинематических параметров показал, что для бесцентрового шлифования и суперфиниширования характерно монотонное изменение окружной и продольной скорости заготовок от максимального значения на входе к минимальному значению на выходе из зоны обработки.
Формообразование поперечного сечения заготовок зависит от исходных отклонений формы и параметров наладки станка, которые определяются взаимным положением заготовки и базирующих элементов. Профиль заготовки с погрешностями формы в поперечном сечении принято описывать тригонометрическим полиномом. Решение задачи микробазирования заготовки позволило сформулировать рекомендации по оптимальному выбору углов контакта заготовки с базирующими элементами. Так как амплитуды и начальные фазы гармоник в партии заготовок имеют стохастический характер, то предложено наладку станков проводить на основе статистического моделирования Монте-Карло.
Неотъемлемой частью общей проблемы обеспечения точности следует считать выявление погрешностей формы поверхностей на этапе измерения. Для исследования отклонений в поперечном сечении тел вращения традиционно используют гармонический анализ. Однако его непосредственное применение не всегда приводит к желаемому результату. Показано, что при наличии эксцентриситета средняя окружность профиля описывается суперпозицией гармоник. При этом основная гармоника однозначно определяет величину эксцентриситета, но сама кривая отличается от синусоиды. Перспективным направлением является бесцентровое измерение отклонения от круглости при создании методики компенсации методической погрешности.
Таким образом, дальнейшее развитие теории, методов и средств бесцентровой абразивной обработки на основе новых математических моделей, ориентированных на последние достижения в области моделирования, численных методов анализа и компьютерной поддержки, призвано способствовать обеспечению и повышению точности обработки.
Далее выполняют преобразование трапецеидального распределения
чисел у1 и у2 в равномерное на интервале [0, 1] по следующим формулам:
если у7 > s1/2, то при р = s2 — у7
Отклонения формы деталей в партии носят стохастический характер. Аналитическое описание отклонений формы в поперечном сечении деталей требуется при статистическом моделировании методом Монте-Карло, который рассмотрен в п. 6.4. Поэтому необходимы экспериментальные исследования для выявления законов распределения составляющих погрешности формы деталей.
Эксперимент проводился в лабораторных и производственных условиях на ОАО «Саратовский подшипниковый завод». Для анализа эмпирического распределения минимальное количество измерений при доверительной вероятности 0,95 составляет 39, согласно работе [82]. Исследовались две партии из 50 заготовок: 1) валиков 016×92 после обработки на бесцентровом круглошлифовальном станке SASL-200×500 (Mikrosa, Германия) и после обработки на бесцентровом суперфинишном станке SZZ-3 (Mikrosa, Г ермания); 2) внутренних колец подшипника 030 после чистовой обработки на бесцентровом шлифовальном станке SWaAGL-50 (VEB Berliner Werk — zeugmachinenfabrik, Г ермания). Измерялись базовые и обрабатываемые поверхности деталей (у внутреннего кольца подшипника базовая поверхность — цилиндрический борт, а обрабатываемая — сферический желоб) на кругломере Talyrond 73. Разрешающая способность измерительного датчика при контроле радиусов на данном приборе составляет 0,025 мкм. Информация с кругломера снималась в цифровом виде и подвергалась гармоническому анализу. Амплитуды гармоник величиной менее 0,01 мкм считались шумом и не учитывались. Также измерялся профиль продольного сечения валиков на профилографе МР 125.
В ходе эксперимента и статистической обработки полученных данных решались следующие задачи:
• идентификация распределений отклонения от круглости, профиля продольного сечения, амплитуд и начальных фаз гармоник поперечного профиля деталей до и после обработки;
• установление корреляционной связи между отклонением от круглости и профилем продольного сечения деталей до и после обработки для анализа вклада геометрической составляющей погрешности формообразования;
• выявление корреляционных связей между отдельными гармониками поперечного профиля в партии деталей.
Задача идентификации распределений решалась на основе положений теории вероятностей и математической статистики [82 — 87]. Вначале экспериментальные данные группировались и строились гистограммы. Затем вычислялись начальные первые четыре статистические момента. На основе этих данных делались выводы о предполагаемых теоретических функциях плотности распределения с использованием различных критериев и диаграмм [56, 83, 85].
Идентификацию плотности распределения можно реализовать с помощью различных программных продуктов для статистического анализа данных [86]. Однако основной недостаток известных пакетов программ связан с ограниченным набором аналитических распределений (обычно 715 для непрерывных распределений). Поэтому разработана программа для идентификации гистограмм случайных величин. База данных включает 30 известных классов непрерывных одномодальных распределений, получивших наибольшее распространение в технике [56, 57, 82, 87], в частности, распределения Вейбулла, Стьюдента, Фишера, Пирсона, Джонсона, логистического, логнормального, P-, у-, z-распределения.
Оценки параметров распределения обычно вычисляют по известным формулам, в большинстве случаев — по методу моментов, который дает асимптотически нормальные оценки. Смещение такой оценки часто удается исключить с помощью простых поправок. Однако такие оценки не являются эффективными, поэтому их использовали только для начального приближения. Уточненные оценки параметров распределений рассчитывались по методу наименьших квадратов, который дает асимптотически эквивалентные оценки по методу максимального правдоподобия [85]. В качестве метода оптимизации выбран метод Хука-Дживса.
Статистические гипотезы о соответствии теоретического и эмпирического распределений проверялись по критерию согласия Колмогорова. Принималась доверительная вероятность 95 %. Критерий Колмогорова в отличие от критерия Пирсона применим для малого объёма выборки, использует результаты наблюдений и не требует построения статистического ряда, что повышает объективность выводов.
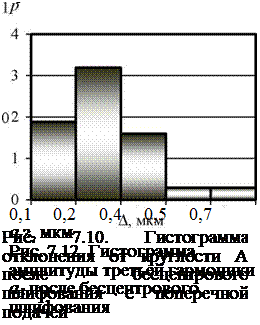
В качестве примеров на рис. 7.10 — 7.13 приведены гистограммы для отклонения от круглости, амплитуды и начальной фазы третьей гармоники после бесцентрового шлифования и суперфиниширования.
Результаты идентификации эмпирических распределений представлены в табл. 7.5. Установлено, что начальные фазы всех гармоник, как при шлифовании, так и при суперфинишировании, имеют равномерное распределение. Такое распределение дает вероятность того, что измеренная величина будет лежать в интервале [0, 360], когда вероятность того, что измеренная величина принадлежит данному интервалу, прямо пропорциональна длине интервала. По этому закону обычно распределены случайные составляющие погрешности измерения, обусловленные сухим трением, погрешностями округления отсчетов по шкале прибора [87].
Амплитуды гармоник распределены по закону Пирсона первого типа (P-распределение). Распределение Пирсона может иметь различную форму
 |
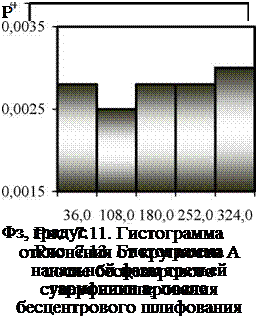 |
и используется для описания большого числа реальных случайных величин, значения которых ограничены конечным интервалом. Распределение Пирсона в большей степени соответствует физической сущности амплитуд гармоник, так как оно ограничено с обеих сторон, в то время как гамма — распределение и логнормальное распределение ограничены только с левой стороны.
Отклонение от круглости, которое представляет собой комплексный параметр, распределено по нормальному или логнормальному законам. С одной стороны, нормальный закон лучше характеризует физическую модель измерения, так как отклонение от круглости есть результат сложения
множества случайных величин. С другой стороны, отклонение от кругло — сти — всегда положительная величина, что в большей степени соответствует логнормальному закону. Поэтому, если математическое ожидание располагается достаточно далеко от нуля или среднеквадратическое отклонение мало, то эмпирическое распределение лучше аппроксимируется нормальным законом. В остальных случаях предпочтительным будет логнормальный закон.
Таблица 7.5
|
Законы распределения отклонений формы деталей при бесцентровом шлифовании и суперфинишировании
|
Полученные параметры распределения для амплитуд гармоник с 2-й по 25-ю приведены: для шлифования с продольной подачей — в табл. 7.6; для шлифования с продольной подачей и суперфиниширования — в табл. 7.7. В табл. 7.6, 7.7 указаны: параметры P-распределения ц и ц; ah a2 — границы интервала изменения.
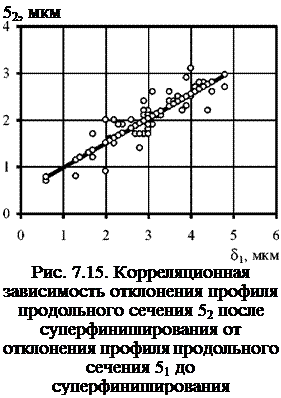
Корреляционный анализ отклонения от круглости и профиля продольного сечения деталей до и после бесцентрового шлифования и суперфиниширования показал, что между этими параметрами имеется прочная связь. Коэффициент корреляции составляет от 0,8 до 0,9. Критическое значение, соответствующие доверительному интервалу для коэффициента корреляции, при n = 50 и доверительной вероятности 95 % равно +0,27 по данным работы [84]. Таким образом, вклад геометрической составляющей в процесс формообразования следует считать существенным. Установленный факт подтверждает высказанное еще в работе [4] положение о склонности процесса бесцентрового шлифования к геометрической наследственности. В качестве примера на рис. 7.14, 7.15 проиллюстрированы корреляционные зависимости для отклонения от круглости А и профиля продольного сечения 5 до и после суперфиниширования. Коэффициент корреляции составил 0,878 и 0,857 соответственно.
|
Таблица 7.6 Параметры распределения амплитуд гармоник при бесцентровом шлифовании
|
|
Таблица 7.7 Параметры распределения амплитуд гармоник при бесцентровом суперфинишировании
|
Исследование корреляционных связей между амплитудами отдельных гармоник профиля деталей показало, что статистическая зависимость между ними слаба. Коэффициент корреляции не превышает +0,07.
Д2, мкм 1 —

 0,8—-
0,8—-
0,6—-
0,4—-
0,2—-
0 —-
0 0,5 1 1,5 2 2,5 3
Дь мкм
Таким образом, статистическая обработка экспериментальных данных по отклонениям формы деталей при бесцентровом шлифовании и суперфинишировании позволила установить законы и параметры распределения, а также корреляционные связи между отдельными составляющими. Полученные результаты подтвердили наличие геометрической наследственности и составили основу для статистического моделирования и наладки станков на обработку партий заготовок с учетом стохастических факторов.
