Математическая модель бесцентрового измерения отклонения от круглости

Бесцентровое измерение профиля деталей относят к разностному способу измерений, при котором измеряют не абсолютные значения инте­ресующей функции, а разность между ее последовательными значениями, разделенными определенным промежутком [58]. Причем аналитическая зависимость между измеряемой и искомой величиной неизвестна.

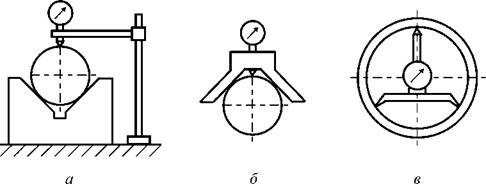
Способ разностного измерения отклонения от круглости конструк­тивно реализован в виде разнообразных комбинаций призм и датчиков ма­лых линейных перемещений. На рис. 7.6 показаны следующие варианты приборов: призма с нерегулируемым положением датчика (а), призматиче­ский «наездник» (б), прибор с мостиками-призмами для контроля внутрен­них поверхностей (в).

Рис. 7.6. Приборы для бесцентрового измерения отклонения от круглости

Наиболее распространены приборы с углом призмы 60, 90 или 120 °, у которых направление измерения совпадает с биссектрисой угла призмы (см. рис. 7.6 а). Известны также призмы с регулируемым углом раскрытия и изменяемым положением датчика. Все эти приборы трехконтактные.

Основная особенность разностных измерений состоит в том, что по­казания прибора Лп связаны со значением фактического отклонения от круглости Л уравнением

Лп ЦЛ,

где р = fa, Р, п) — коэффициент пропорциональности (коэффициент вос­произведения); а — угол призмы; Р — угол, определяющий положение дат­чика относительно биссектрисы угла призмы; п — номер гармоники.

Конкретный прибор с фиксированными значениями углов а и Р име­ет различные коэффициенты воспроизведения для разных гармонических составляющих отклонения формы профиля детали. Поскольку обычно профиль детали описывается не одной гармоникой, а их суммой с отлич­ными амплитудами и начальными фазами, то установление коэффициента ц — сложная математическая задача. Поэтому с помощью трехконтактных приборов можно лишь приближенно судить об отклонении от круглости измеренной детали. По различным данным [61, 76], погрешность измере­ния составляет 100 % и более. Данную погрешность по существующей терминологии классифицируют как методическую, то есть присущую са­мому методу измерения.

Коэффициент воспроизведения ц меняется в широких пределах в за­висимости от вида отклонений формы измеряемой детали, в ряде случаев он равен нулю. Это объясняется тем, что в процессе измерения деталь ба­зируется по плоскостям призмы непосредственно измеряемой поверхно­стью. Погрешность базирования приводит к изменению положения центра профиля и соответственно расстояния до измерительного датчика. Эти из­менения прибор воспринимает так же, как и отклонения формы поверхно­сти. Например, при контроле детали в форме эллипса на призме с углом 60° прибор не зафиксирует отклонения от круглости, коэффициент вос­произведения будет равен нулю. При аналогичном измерении детали с трехгранной формой показания прибора в три раза превысят действитель­ное значение отклонения от круглости, коэффициент воспроизведения бу­дет равен трем.

Таким образом, бесцентровое измерение на призме с датчиком ма­лых линейных перемещений рекомендуют применять только в двух случа­ях [58]:

• если расчетным или экспериментальным путем установлено, что мето­дическая погрешность измерения существенно меньше допуска на от­клонение от круглости детали;

• если измерение проводят путем сравнения контролируемой детали с образцовой, а отклонения нормируют непосредственно в значениях по­казаний конкретного прибора.

Последний случай удобен для массового производства, что объясня­ет широкое применение трехконтактных приборов в автомобильной и подшипниковой промышленности.

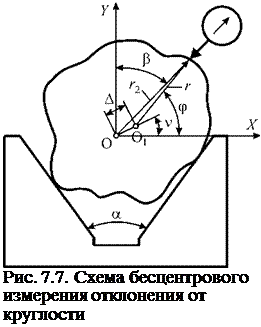
Рассмотрим процесс бесцентрового измерения отклонения от круг­лости на призме с углом раскрытия а и направлением измерения, состав­ляющим угол Р с биссектрисой угла раскрытия (рис. 7.7). Полагаем, что датчик перемещается только вдоль направления измерения, заданного уг­лом р.

Аналитическое описание измерения раскладывается в три этапа: находится центр средней окружности профиля после базирования, опреде­ляются радиусы измеренных датчиком точек профиля, рассчитывается от­клонение от круглости [77].

Первый этап выполняют аналогично рассмотренному в п. 4.1 бесцен­тровому базированию на неподвижных опорах. Отличия заключаются лишь в используемых обозначениях, поэтому приведем результаты без по­дробных пояснений.

Считаем, что деталь одновременно и постоянно находится в точеч­ном контакте с обеими гранями призмы. Поэтому отклонения формы в точках контакта стремятся сместить деталь по направлениям углов у1 и у2, фактическое же смещение происходит вдоль граней призмы. Таким обра­зом, деталь последовательно перемещается по граням призмы на величины Аі и А2, которые представляют собой проекции AJ и А2 на угол а/2:

lAj = A[[sin( Yj + а / 2) + cos( ух + а / 2 )ctga

[Аз = А2 sin( у 2+а / 2 ) + cos( у2 + а / 2 )ctg а}

Положение центра О1 детали после смещения по граням призмы найдем векторным сложением смещений А1 и А2. Радиус-вектор центра О1 профиля определим по формуле:

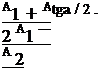А = ч]А1 + А22 — 2 А А cos а;

На втором этапе определяют радиус r2 измеренных точек профиля детали после базирования. Исходными данными являются координаты (А, v) центра средней окружности профиля и радиусы r профиля детали. Уста­новление аналитической зависимости между радиус-векторами r2 и r при­водит к громоздким математическим выкладкам и, в конечном счете, к ре­шению трансцендентного уравнения. Точность определения вектора r2 непосредственно зависит от точности решения трансцендентного уравне­ния, то есть от числа точек на профиле детали.

Поэтому воспользуемся численным методом, который заключается в следующем. Так как измерительный датчик перемещается только вдоль направления, заданного углом Р, то он регистрирует точку, наиболее близ­ко расположенную к данной прямой. Таким образом, задача сводится к по­иску точки профиля, имеющей кратчайшее расстояние d до направления перемещения датчика:

d ^ min.

Расстояние d представляет собой длину перпендикуляра, опущенно­го из точки профиля на прямую. Прямая перемещения датчика проходит через начало системы координат и ее уравнение y = кх, где к = tg(90° — Р). Расстояние d вычисляют по известной формуле:

(7.13)

где (хи y) — декартовы координаты i-й точки профиля детали. Декартовы координаты i-й точки профиля:

В результате расчетов по формулам (7.11) — (7.13) получаем изме­ренный профиль в декартовой системе координат. Сделав преобразования координат из декартовой в полярную систему, получим искомую кругло — грамму.

На третьем этапе определяют отклонение от круглости — максималь­ное расстояние от точек профиля до средней окружности. Если центр средней окружности круглограммы совпадает с началом системы коорди­нат, то отклонение от круглости есть разность максимального и минималь­ного радиусов. В противном случае требуется дополнительно определить параметры средней окружности, а затем отклонение от круглости.

Изложенная методика расчета бесцентрового измерения отклонения от круглости реализована в виде программы на языке C++, интерфейс ко­торой показан на рис. 7.8.

Несмотря на использование численных методов решения в задаче измерения, возможности современной вычислительной техники позволяют обеспечить высокую точность. Так, при задании профиля 1000 точками полученная точность измерения, проверенная решением обратной задачи, не превышает 0,5 % от действительной величины отклонения от круглости.

Представляет интерес сравнение результатов расчета по предложен­ной математической модели бесцентрового измерения с данными, приве­денными в работе [78]. В табл. 7.3 даны коэффициенты воспроизведения первых 12 гармоник прибором с параметрами а = 90° и Р = 7,5°. При рас­чете по формулам (7.11) — (7.13) радиус средней окружности профиля при­нят r0 = 10 мм.

Н В II 4?

Положение датчика

Расстояние от центра |15 Угол установки КО

Угол призі-

Параметры анимации Р" Координатная сетка Г" Начальное положений

Р" Смещённое положені Р" Траектория центра р" Вектор центра р" Измеренный профилі

Параметры заготовки

Средний радиус [ТО

Амплитуда | Кр. частота [ Нач. фазаГ|

64,9000000.

84.3999999.

Рис. 7.8. Интерфейс программы бесцентрового измерения отклонения от круглости

Таблица 7.3

Коэффициенты воспроизведения при бесцентровом измерении
прибором с параметрами а = 90° и Р = 7,5°

Номер гармоники	По формулам (7.11) — (7.13)	По данным [78]
an = 0,5 мм	an = 0,05 мм	an = 0,005 мм
2	1,092	1,069	1,071	1,064
3	1,873	1,924	1,929	1,932
4	0,791	0,755	0,757	0,733
5	1,791	1,919	1,921	1,932
6	0,919	0,874	0,872	0,879
7	0,976	1,047	1,048	1,000
8	1,472	2,055	2,051	2,090
9	0,916	1,044	1,043	1,000
10	1,109	1,203	1,194	1,179
11	1,041	1,361	1,362	1,414
12	1,074	1,722	1,767	1,732

Анализ табл. 7.3 показал, что расхождение результатов в среднем со­ставляет 5 %, только для случая с амплитудой гармоники an = 0,5 мм отли­чие достигает 10 %. Погрешность модели [78] вызвана допущением о том, что точки контакта детали с плоскостями призмы всегда находятся на пер­пендикулярах к соответствующим граням призмы, проведенным через центр средней окружности профиля в исходном положении. Такая поста­новка задачи позволила получить формулы для коэффициента воспроизве­дения в явном виде, но без учета влияния радиуса средней окружности профиля. В общем случае точки контакта не удовлетворяют указанному условию, а величина смещения центра средней окружности нелинейно за­висит от амплитуды гармоники. Данный факт легко понять из следующих рассуждений: если максимальное смещение происходит не по нормали к грани призмы, то проекция величины смещения будет зависеть от его уг­лового расположения. При этом соотношение радиуса средней окружности и амплитуды гармоники влияет на угловое расположение смещения и тем самым определяет величину проекции. Именно с учетом данного обстоя­тельства в табл. 7.3 приведены коэффициенты воспроизведения, рассчи­танные для трех амплитуд гармоник при едином радиусе средней окруж­ности профиля. Другой недостаток модели [78] — возможность исследовать коэффициент воспроизведения только для одной гармоники. Однако изме­ренный профиль даже для одной гармоники представляет собой кривую, отличную от консинусоиды, которая при гармоническом анализе дает не­которую сумму различных гармоник. Справедливости ради можно отме­тить, что наибольшую амплитуду имеет именно гармоника того же номера, что и исходная. Характерная особенность при анализе отдельных гармоник заключается в том, что измеренная кривая имеет центр средней окружно­сти, совпадающий с центром средней окружности действительного профи­ля.

В качестве примера в табл. 7.4 приведены коэффициенты воспроиз­ведения для призмы с углом 60, 90 и 120° при различных угловых положе­ниях датчика. Радиус средней окружности принят r0 = 10 мм, а амплитуды 2-, 3-, 4- и 5-й гармоник равны 1 мм.

Данные табл. 7.4 дают общее представление о коэффициентах вос­произведения гармоник при различных сочетаниях угла призмы и углового положения датчика. Приведенные результаты помогают установить диапа­зон погрешностей измерения отклонения от круглости и дать рекоменда­ции при измерении деталей с известной априори доминирующей гармони­кой. Коэффициент воспроизведения принимает значения как больше еди­ницы (амплитуда гармоники измеряется с увеличением), так и меньше единицы (амплитуда гармоники измеряется с уменьшением). Однако даже при коэффициенте воспроизведения, равном единице, измеренный про­филь отличается от фактического, поэтому получение такого значения ко­эффициента ц не решает полностью задачи правильного измерения. Ос­новной позитивный вывод, который можно сделать из приведенного ана­лиза, заключается в том, что процесс бесцентрового измерения на уровне моделирования управляем.

Таблица 7.4

Коэффициенты воспроизведения при бесцентровом измерении а, градус 3, градус 0 10 20 30 40 50 60 70 80 n = 2 60 0,130 0,544 1,025 1,436 1,749 1,941 2,000 1,921 1,712 90 1,000 1,144 1,397 1,669 1,910 2,077 2,146 2,105 1,955 120 1,567 1,651 1,821 2,013 2,187 2,311 2,361 2,324 2,196 n = 3 60 3,000 2,870 2,517 1,985 1,347 0,700 0,212 0,632 0,919 90 1,947 1,824 1,485 0,966 0,330 0,378 1,014 1,534 1,865 120 1,000 0,883 0,571 0,227 0,752 1,382 2,005 2,529 2,880 n = 4 60 0,214 0,615 1,081 1,353 1,676 1,933 1,990 1,871 1,635 90 0,464 0,926 1,469 1,872 2,017 1,872 1,466 0,974 0,870 120 0,551 1,054 1,668 1,999 1,919 1,493 0,870 0,685 1,219 n = 5 60 0,527 1,182 1,833 1,864 1,407 0,790 0,343 1,050 1,672 90 1,738 1,751 1,410 0,862 0,467 0,535 1,073 1,554 1,807 120 1,787 1,589 0,959 0,226 0,963 1,612 1,896 1,716 1,122

Вопросы выбора угловых параметров приборов для бесцентрового измерения отклонения от круглости подробно рассмотрены в работе [79]. Согласно приведенным в ней данным (а также табл. 7.4), обеспечить еди­ный коэффициент воспроизведения для первых 10 — 20 гармоник не пред­ставляется возможным.

В настоящей монографии поиск оптимальных углов призмы и распо­ложения датчика для различных гармоник не выполнялся, так как он ли­шен практического смысла. При анализе коэффициента воспроизведения реального профиля в виде суммы многих гармоник принцип суперпозиций не выполняется даже при нулевых начальных фазах гармоник. Кроме того, возникает эксцентриситет центров средних окружностей действительного и измеренного профилей.

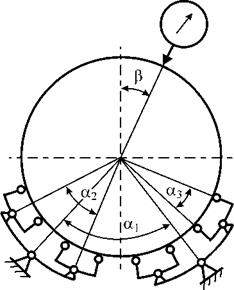
Известны два способа улучшения результатов бесцентрового изме­рения отклонения от круглости. Первый основан на одновременном ис­пользовании двух призм с разными углами раскрытия [80]. Показания установленных в призмах датчиков корректируются и суммируются. В ре­альном приборе с углами а = 60, 120° воспроизводятся с искажением в пределах 10 % гармоники с 3- по 9-ю и с 15- по 22-ю, с коэффициентом воспроизведения 0,5 — 2-, 10- и 14-я гармоники, а 11-, 13-, 23- и 25-ю гар­моники прибор не улавливает.

Другой способ — применение специальной многозвенной призмы (рис. 7.9). Подбором углов раскрытия звеньев удается обеспечить близкие к единице коэффициенты воспроизведения для значительного числа гар­моник.

Рис. 7.9. Схема накладного кругломера с самоустанавливающимися многозвенными призмами

По данным работы [81], накладной кругломер с параметрами а1 = 78, а2 = 40, а3 = 20 и Р = 180° позволяет воспроизвести первые 25 гармоник с погрешностью 25 — 30 %. Пятизвенная конструкция уменьшает погреш­ность для всех 25 гармоник, кроме 3-й, в пределах 8 % (для 3-й гармоники погрешность составляет 17 %).

Полностью устранить методическую погрешность, свойственную бесцентровому методу измерения, можно лишь расчетным путем. Данный вопрос не раз поднимался в научных публикациях, однако до настоящего времени не нашел строгого решения. По мнению ряда авторов, информа­ции от одного измерительного датчика для анализа не достаточно. Однако постоянное развитие вычислительной техники позволяет надеяться, что в ближайшем будущем проблема бесцентрового измерения отклонения от круглости будет решена.