Повышение точности измерений при радиусном и координатном методах достигается минимизацией эксцентриситета между центром средней окружности профиля и началом измерительной системы. Поэтому в первом случае деталь предварительно центрируют, а во втором — математически определяют положение центра средней окружности профиля. Метод разностного измерения дополнительно требует минимизации перемещений центра средней окружности при вращении детали относительно измерительного датчика.
Современные кругломеры оснащены точными механизмами центрирования (номинальная точность — до 0,01 мкм). При этом стандартная методика центрирования на кругломерах [59] основана на минимизации функционала G:
2п
G =J(r} — e)dy, (7.1)
0
когда вначале находят длину е радиус-вектора эксцентриситета, а затем соответствующие ему координаты (x, у) центра средней окружности, при которых Gmin принимает наименьшее значение.
Однако действительная точность центрирования по радиальному биению зависит, в первую очередь, от характера отклонений профиля измеряемой детали и от радиуса вращения датчика, который в общем случае не равен априори неизвестному радиусу средней окружности профиля. Кроме того, предварительное центрирование, даже при автоматизации этой про
цедуры, занимает в несколько раз больше времени, чем собственно измерение.
Широкое применение в производственной практике благодаря своей простоте получили формулы Спрегга [60] для расчета радиуса R и координат (x, у) центра средней окружности:
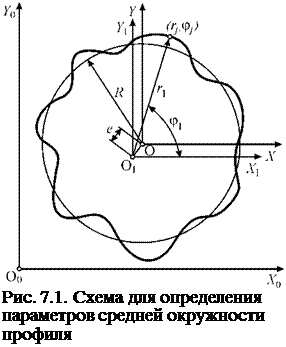 |
где rj — радиус j-й точки профиля; Xj, yj — декартовы координаты j-й точки профиля; n — число измеренных точек профиля (рис. 7.1).
Во многих работах [62, 63] отмечен приближенный характер формул (7.2), которые дают хорошие результаты только при небольших эксцентриситетах. Формально требуется выполнение условия е << R, то есть необходимо предварительное центрирование деталей. Однако более строгие данные о погрешностях формул (7.2) отсутствуют.
Основные положения для расчета параметров базовых окружностей при координатных измерениях приведены в стандарте [64]. Математически строгое центрирование предполагает определение трех параметров — радиуса R и координат (x, y) центра средней окружности. Указанные параметры находят из условия минимума функционала Ф, представляющего собой сумму квадратов расстояний от измеренных точек (xj, yj) до средней окружности [65]:
ф(х, уЛ) = Z(V(xj ~ x) + (Уі ~ У)2 ~ RУ. (7.3)
j=i
Процедура минимизации функционала Ф реализуется итерационными методами, что обусловливает ее высокую трудоемкость. Поэтому данный метод получил применение только при измерении на КИМ.

рования на точность измерения отклонения от круглости с помощью гармонического анализа справедливы также и при использовании формул Спрегга.
Оценим погрешность представления эксцентриситета средней окружности в виде первой гармоники при анализе профиля детали.
Уравнение средней окружности профиля детали с центром О в системе координат (Х1 Оі Y1) (рис. 7.2):
![]() Xj = Rcosty + ecos у;
Xj = Rcosty + ecos у;
Yj = Rsinty + esiny,
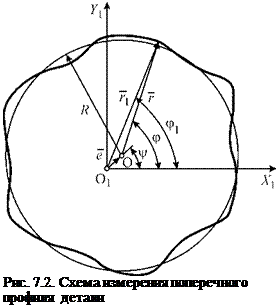 |
где ф — полярный угол в системе координат с полюсом О; у — полярный угол радиус-вектора эксцентриситета е.
Уравнение окружности (7.6) в полярной системе координат с полюсом О1 получим на основе известных преобразований:
![]() r, = V X, + Yj2;
r, = V X, + Yj2;
Фі = arctg(Yj / Xj),
где ф1 — полярный угол в системе координат с полюсом О1.
 |
|
Гармонический анализ подразумевает задание профиля конечным множеством точек с равномерным угловым расположением относительно начала системы координат. Для выполнения этого условия установим связь между углами ф и ф1 из второго уравнения (7.7):
Особенность формулы (7.9) заключается в равномерном угловом расположении точек на профиле при наличии эксцентриситета.
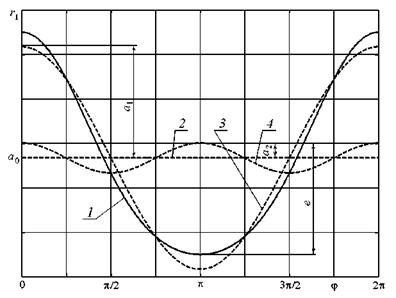
На рис. 7.3 приведен пример, изображающий среднюю окружность 1 с эксцентриситетом е и характеризующие окружность первую гармонику 2, вторую гармонику 3 и третью гармонику 4.
|
Рис. 7.3. Гармонический анализ средней окружности профиля |
Гармонический анализ выражения (7.9) выполнен численным методом, так как решение в явном виде приводит к громоздким математическим выкладкам. Установлено, что функция, заданная уравнением (7.9), описывается суперпозицией нулевой, первой и четных гармоник (p = 1, 2, 4, …) с амплитудами, быстро убывающими при увеличении номера гармоники. Значимыми можно считать только амплитуды нулевой а0, первой а1 и второй а2 гармоник. Первая гармоника однозначно определяет амплитуду e и начальную фазу у эксцентриситета, хотя при этом развертка эксцентрической окружности отличается от синусоиды. Из результатов гармонического анализа также следует, что амплитуда а0 нулевой гармоники меньше радиуса R средней окружности на величину амплитуды а2 второй гармоники.
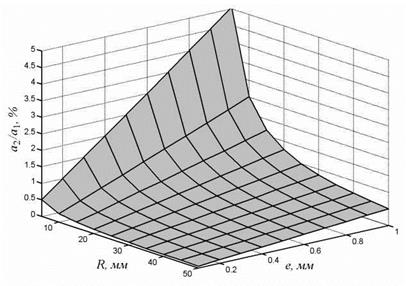
Амплитуда а2 второй гармоники нелинейно связана с амплитудой а1 первой гармоники (рис. 7.4). Соотношение амплитуд а2/а1 существенным образом зависит от отношения е/R. Так, например, максимальное значение а2/а1 = 0,42 достигается при эксцентриситете, равном радиусу средней окружности. В диапазоне е/R < 0,1 зависимость а2/а1 близка к линейной и указанное отношение составляет примерно 0,025. Если круглограмма анализируется графическим способом, где вместо радиуса детали рассматривают средний радиус записи, в большей степени соизмеримый с эксцентриситетом, то отклонения будут в несколько раз больше.
|
Рис. 7.4. Зависимость амплитуд первой и второй гармоник средней окружности |
Таким образом, компенсацию методической погрешности центрирования следует осуществлять, вычитая из измеренных длин радиус-векторов точек профиля r1 корректирующую добавку Ar, представляющую собой сумму первой и второй гармоник и разность амплитуды второй гармоники: r = r — Ar = r — a cos(ф-Vi)+а2[1 — cos(2ф-^)]. (7.10)
В выражении (7.10) величины а1, ^1 определяют на основании гармонического анализа профиля детали по формулам (7.5), а величину а’ — на основании гармонического анализа эксцентрической средней окружности по выражению (7.9). Радиус средней окружности R рассчитывают как сумму нулевой гармоники а0 и амплитуды а’ второй гармоники.
Рассмотренная методика, использующая формулы (7.9), (7.10), прошла апробацию и получила применение в разработанном способе измерения на кругломерах [70].
Проведем сравнительный анализ точности измерения отклонения от круглости при стандартном и предложенном методах в зависимости от точности центрирования. Экспериментально полученные круглограммы подвергались гармоническому анализу и статистической обработке, а затем моделировались по методу Монте-Карло. При гармоническом анализе учитывались гармоники со 2-й по 25-ю включительно, причем гармоники с амплитудами менее 0,01 мкм не рассматривались. Установлено, что амплитуды гармоник распределены по закону Пирсона первого типа, начальные фазы — по закону равных вероятностей, а отклонение от круглости — по нормальному закону. Аналогичные результаты были получены в работе [71] для отверстий диаметром 1 мм, полученных вырубкой, калибровкой и сверлением.
Моделирование круглограмм с указанными законами распределения проведено по статистическому методу Монте-Карло (рассмотрен в п. 6.4). Корреляция амплитуд и начальных фаз для отдельных гармоник не учитывалась. Профиль круглограммы задавался 500 точками (в соответствии с данными прибора Talyrond 73). Также моделировалась случайная погрешность центрирования: радиус е, распределенный по нормальному закону, полярный угол у, распределенный по закону равных вероятностей. Далее рассчитывалось отклонение от круглости по формуле (7.2) для известной и по формуле (7.10) для предложенной методики и проводилась статистическая обработка.
В табл. 7.2 приведены результаты моделирования при измерении отклонения от круглости 500 круглограмм в виде оценок математического ожидания x и среднеквадратического отклонения а, полученных для трех значений погрешности центрирования. Результаты расчетов округлялись до практически значимой величины 0,01 мкм.
Таблица 7.2
|
Результаты моделирования измерения отклонения от круглости
|
Анализ табл. 7.2 показал, что при погрешности центрирования 0,01 мм стандартная методика дает точный результат, при 0,05 мм — удовлетворительный, а при 0,2 мм — неудовлетворительный результат. Рассчитанное по предложенной методике отклонение от круглости совпало с действительным с принятой точностью 0,01 мкм при всех значениях погрешности центрирования.
Таким образом, практическое применение разработанной методики для обработки результатов измерения на кругломерах позволяет снизить требования к точности центрирования в 5.. .10 раз и тем самым увеличить производительность измерения.
Рассмотренная методика применима при координатном и разностном способе измерения, а также при измерении диаметров деталей [72 — 75].
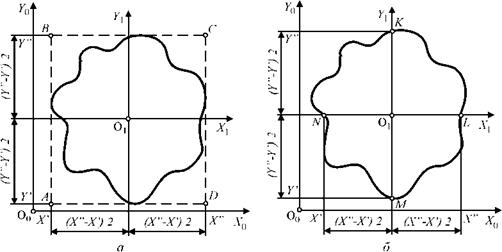
При координатном способе целесообразна следующая последовательность измерения и обработки результатов. С помощью КИМ находят координаты точек поперечного профиля в системе координат (X0 О0 70) измерительной машины, выбирают приближенный центр О і средней окружности профиля. За приближенный центр О1 средней окружности принимают, например, центр прямоугольника ABCD, охватывающего про-
филь детали (рис. 7.5 а). Также за приближенный центр Оі средней окружности можно принять точку, делящую пополам каждый из двух взаимно перпендикулярных отрезков KM и LN, ограниченных противолежащими точками K, M,, L, N профиля (рис. 7.5 б). Отрезки KM и LN не обязательно параллельны осям X0, Y0.
|
Рис. 7.5. Приближенный выбор центра средней окружности профиля при координатном способе измерения отклонения от круглости |
Далее проводят гармонический анализ координат (ту ф7) точек профиля в системе координат (X1 О1 Y1), на основании которого получают радиус R и уточненное положение центра О средней окружности профиля, определяемое координатами (e; ф). Затем координаты (х{, у) точек профиля пересчитывают по известным формулам:
X} = TjCOSi^ J + ecos фЛ
Y = т^їпф J + esinф. І
При этом последующее неравномерное угловое расположение точек на профиле при расчете отклонения от круглости значения не имеет. Однако выявление гармонических составляющих погрешности в таком случае затруднено.
При разностных измерениях, когда эксцентриситет имеет постоянное значение, гармонический анализ позволяет уменьшить методическую погрешность в несколько раз в зависимости от условий измерения. Это достигается математической компенсацией погрешности базирования детали относительно шпинделя и биения самого шпинделя измерительного устройства. Особенно целесообразно использование данной методики при измерении в процессе обработки детали без предварительного центрирования [67]. Рассмотренный метод получил апробацию при измерении диаметра и отклонения от круглости валов на прецизионных токарных станках типа ТПК-125ВН2. При этом погрешность измерения отклонения от круглости уменьшилась в 2.. .3 раза.