Наладка станков по критерию точности базирования на основе статистического моделирования Монте-Карло

Налаживать бесцентровые шлифовальные и суперфинишные станки на обработку одной конкретной заготовки нецелесообразно, а в партии от­
клонения формы заготовок имеют стохастический характер. Выявить одну доминирующую гармонику не всегда возможно, как правило, имеются не­сколько гармоник со сравнительно большими амплитудами. Для решения подобных задач предназначен метод статистического моделирования, так же называемый методом статистических испытаний Монте-Карло [55]. Он базируется на применении случайных чисел некоторой случайной величи­ны с заданным распределением вероятности. Сущность метода статистиче­ского моделирования сводится к построению моделирующего алгоритма, его реализации с помощью программно-технических средств ЭВМ и обра­ботке данных методами математической статистики.

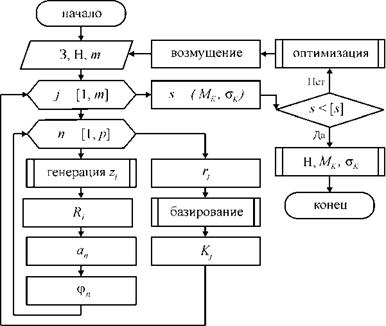
Применительно к задаче базирования основная идея метода Монте- Карло заключается в моделировании стохастических входных данных (от­клонений формы заготовок), многократной реализации аналитической мо­дели базирования и получении вероятностных характеристик, численные значения которых совпадают с результатом решения детерминированной задачи. В результате получают серию частных значений искомой погреш­ности базирования, статистическая обработка которых дает сведения о влиянии параметров наладки станка при обработке партии заготовок. Ис­ходные данные о погрешностях формы заготовок устанавливают экспери­ментальным путем, а затем находят законы и параметры распределения (см. п. 7.4). Если количество реализаций достаточно велико, то получен­ные результаты моделирования приобретают статистическую устойчи­вость и с достаточной точностью принимаются в виде оценок искомых па­раметров. Моделирующий алгоритм приведен на рис. 6.9.

Рис. 6.9. Моделирующий алгоритм для наладки станка при обработке партии заготовок

Исходными данными при моделировании являются: параметры заго­товки З (радиус r0, число n гармоник, параметры распределения и границы интервала амплитуд и начальных фаз гармоник), параметры наладки стан­ка (углы базирующих элементов, радиусы валков) и количество m загото­вок в партии. Число m заготовок в партии назначают, исходя из трудоем­кости моделирования, а не из реального технологического процесса. Оче­видно, что с увеличением число реализаций m возрастает точность и до­стоверность получаемых статистических оценок.

Первый этап — генерирование последовательности случайных равно­мерно распределенных чисел z, для каждой заготовки в партии в зависимо­сти от числа гармоник профиля. Полученные числа zt преобразуют в тре­буемый закон распределения для амплитуды а, и начальной фазы ф, каж­дой гармоники. В результате формируется профиль одной заготовки rj.

На втором этапе рассчитывают погрешность базирования для каждой заготовки по аналитической модели, описанной в п. 5.1 — 5.3, и находят критерий точности базирования Kj.

На третьем этапе проводят статистическую обработку критерия K, вычисленного для всех заготовок в партии. В результате получают матема­тическое ожидание МК и среднеквадратическое отклонение ак для крите­рия K. Сравнивая их с допустимыми значениями [МК] и [ак], принимают решение о необходимости оптимизации наладочных параметров станка.

Для генерирования случайных чисел с заданным законом распреде­ления используется метод инверсии [55], заключающийся в формировании последовательности случайных чисел z,, равномерно распределенных в ин­тервале [0, 1], и последующем преобразовании:

Л-,. = Fzt), (6.17)

где Fl(z) — функция, обратная функции распределения случайной величи­ны Л,.

Результаты статистического моделирования существенно зависят от качества исходных последовательностей случайных чисел. На практике используют три основных способа генерации случайных чисел: аппарат­ный (физический), табличный (файловый) и алгоритмический (программ­ный). Достоинства и недостатки трех перечисленных способов получения случайных чисел представлены в табл. 6.1.

Из табл. 6.1. видно, что алгоритмический способ генерации случай­ных чисел наиболее рационален при моделировании на компьютере. Рав­номерно распределенная случайная величина в интервале [0, 1] имеет ма­Л

тематическое ожидание m = 1А и дисперсию а = 1/12. Получить непрерыв­ное распределение на ЭВМ невозможно, поэтому используют дискретную последовательность 2n случайных чисел того же интервала. Такой закон распределения называют квазиравномерным распределением. Случайная величина, имеющая квазиравномерное распределение в интервале [0, 1], принимает значения zt = i/(2” — 1) с вероятностями pi = 1/2”, i = 0, …, 2” — 1. В результате математическое ожидание квазиравномерной случайной ве­личины совпадает с математическим ожиданием равномерной случайной последовательности интервала [0, 1], а дисперсия отличается множителем (2” + 1)/(2” — 1), который при достаточно больших n близок к единице. Кроме того, для получения значений zi используют формулы (алгоритмы), поэтому такие детерминированные последовательности чисел называют псевдослучайными.

Таблица 6.1

Сравнительный анализ способов генерации случайных чисел [55]

Способ	Достоинства	Недостатки
аппаратный	1) запас чисел не ограничен 2) расходуется мало операций вычислительной машины 3) не занимает место в памяти вычислительной машины	1) требуется периодическая проверка 2) нельзя воспроизводить по­следовательности 3) используется специальное устройство 4) необходимы меры по обес­печению стабильности
табличный	1) требуется однократная проверка 2) можно воспроизводить по­следовательности	1) запас чисел ограничен 2) занимает много места в оперативной памяти или необходимо время на обра­щение к внешней памяти
алгоритмический	1) требуется однократная проверка 2) можно многократно вос­производить последова­тельности 3) занимает мало места в па­мяти машины 4) не используются внешние устройства	1) запас последовательности чисел ограничен ее перио­дом 2) существенные затраты ма­шинного времени

В нашем случае требуется последовательность из примерно 2-105 случайных чисел. Такой объем псевдослучайных чисел с определенным числом разрядов без повторений обеспечивает стандартный датчик слу­чайных чисел random, имеющийся в большинстве языков и сред програм­мирования. С целью улучшения качества последовательностей после гене­рирования партии заготовок применяется метод возмущений, программно реализованный в виде команды randomize. Эта функция позволяет избе­жать повторения результатов при многократных запусках программы.

Экспериментальные исследования установили, что между некоторы­ми амплитудами гармоник имеются сильные корреляционные связи. Для

2p[1] [2] [3]

S2 — S1 + 4P 2(S1 + S2 ) ’

случайных погрешностей x и у с разными функциями распределения F(x), F2(y), математическими ожиданиями mx, my и среднеквадратическими от­клонениями ах оу целесообразно перейти к равномерно распределенным в интервале [0, 1] случайным величинам, воспользовавшись преобразовани­ями:

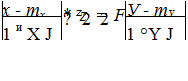
(6.18)

Для выражений (6.20) можно строго доказать, что коэффициентом корреляции между случайными величинами у1 и у2 является r*, если значе­ние г* определялось обычным образом. Числа у1 и у2 в общем случае рас­пределены по симметричному трапецеидальному закону с большим

если Уі < S1/2, то при р = у7

В результате получаем случайные числа z1 и z2, равномерно распре­деленные в интервале [0, 1] и имеющие, как показала соответствующая численная проверка, коэффициент корреляции |г|, связанный с |r*| соотно­шением

|r*| = |r| + 0,005086 + 0,01739sin(6,3986|r| + 5,9575). (6.23)

Таким образом, чтобы найти требуемое значение коэффициента кор­реляции r между случайными величинами z1 и z2, необходимо при форми­ровании случайных чисел y1, y2 задать величину |r*| по выражению (6.23). Абсолютная систематическая погрешность значения r при этом методе по­лучения двух коррелированных выборок не превышает 0,0025.

При перестановках в формулах (6.20) двух пар параметров А и В, А и С случайные величины z1 и z2 будут иметь коэффициент корреляции 1 — |r|, что позволяет сформировать выборки двух случайных величин с коэффи­циентом корреляции +(1 — |r|) и произвольными законами распределения.

Суммируемые случайные погрешности можно разделить на некорре­лированные между собой группы трех типов: включающие любое число некоррелированных погрешностей; жестко коррелированных между собой погрешностей с r = +1 относительно какой-либо одной погрешности из этой группы, принятой за базовую; погрешностей с коэффициентом корре­ляции пар относительно одной базовой погрешности +r и +(1 — |r|). Групп второго и третьего типов может быть несколько, а значение r в каждой из них — произвольным. Если количество погрешностей в группе больше двух, то накладываются ограничения на перекрестные коэффициенты кор­реляции. Например, нельзя одновременно задать значения r12 = 1 и r13 = 1, если r23 Ф 1.

Количество случайных чисел, используемых для получения стати­стически устойчивой оценки параметров при реализации на ЭВМ, колеб­лется в широких пределах в зависимости от объекта моделирования, оце­ниваемых параметров, необходимой точности и достоверности результатов моделирования.

Приближенное число испытаний при моделировании методом Мон­те-Карло определим по формуле из работы [56]:

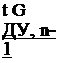I — — Й

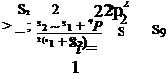(6.18)

где t’дУ, n -1 — коэффициент для вычисления двустороннего доверительного интервала для математического ожидания; e — допустимая ошибка при оценке G.

Для определения допустимой погрешности e воспользуемся неравен­ством Чебышева, согласно которому для любого распределения с конеч­ным математическим ожиданием М и дисперсией а по крайней мере [1 — (1/к)]100 % значений случайной величины находится в интервале М + ка. Пределы по данному выражению задаются с очень большим запа­сом. Считая, что не менее 99 % числа испытаний должны попасть в интер­вал М + 3а, принимаем максимально допустимую ошибку e при оценке М в 0,2а. Максимальное среднеквадратическое отклонение для амплитуд гармоник составляет 0,1 мкм, поэтому назначаем e = 0,02 мкм. При 99 %- ном доверительном уровне и ориентировочном числе испытаний n = 200, получаем їду, n. 1 = 2,601. Число испытаний по формуле (6.18) равно n = = 169. Принимаем число заготовок в партии при моделировании m = 200. Тогда с 99 %-ной вероятностью не менее 99 % от числа испытаний при моделировании попадет в интервал 0,1 + 0,06 мкм.

Экспериментальные исследования (см. п. 7.4) выявили, что амплиту­ды а гармоник распределены по закону Пирсона первого типа (Р — распределение) или логнормальному закону, а начальные фазы ф — по за­кону равной вероятности.

Функция плотности вероятности Р-распределения имеет вид:

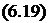
Г( р + д) Г( р)Г(д)

где Г — гамма-функция; р, д — параметры Р-распределения; x — случайная величина.

Известная гамма-функция:

ад

Г(у) = | x ‘^e^dx.

0

Функция распределения начальных фаз гармоник имеет вид:

F(x) = (x — a)/(b — а),

где a, b — границы интервала изменения начальной фазы ф.

Так как а = 0°, b = 360°, то имеем следующее выражение для функ­ции распределения начальных фаз:

F(x) = xt/ 360. (6.21)

В общем случае, зная плотность вероятности f(x), требуется выбрать случайное число zt и решить относительно xi интегральное уравнение:

xi

j f(x,)dxi = z,,

a

где a — наименьшее значение xt.

Для равномерного распределения обратная функция имеет явный вид, и преобразование случайной величины Zi в случайную величину xt осуществляют по выражению:

x = 360z. (6.22)

Методика получения случайных величин, имеющих различные зако­ны распределения, с помощью нормированных случайных величин изло­жена в работах [56, 57].

Параметры P-распределения ц и ц, полученные в результате стати­стической обработки экспериментальных данных, имеют нецелые значе­ния. Поэтому применим метод генерации, предложенный в работе [57]. Вычислим

О _ _1 / Ц О _ _1 / Ц S1 Z1 , «

где z, z2 — независимые друг от друга равномерно распределенные случай­ные числа.

Если S + S2 > 1, то возьмем еще одну пару случайных чисел z, z2 и проделаем те же операции. Если S + S2 < 1, то

Полученные по формулам (6.23) — (6.26) распределения являются нормированными, то есть находятся в интервале [0, 1]. Получить распре­деления в интервале [a, а2] можно с помощью последующего преобразо­вания:

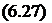у — а

i

а2 — ах

На основе разработанного алгоритма (рис. 6.9), формул (6.19) — (6.27) и экспериментальных данных из п. 7.4 проведено моделирование критерия точности базирования для партии из 200 заготовок для трех слу­чаев: бесцентрового шлифования с продольной подачей, бесцентрового шлифования с поперечной подачей и бесцентрового суперфиниширования. Статистическая обработка результатов показала, что наилучшим образом критерий К описывается нормальным законом при преимущественном P — распределении амплитуд гармоник (бесцентровое шлифование с продоль­ной подачей и бесцентровое суперфиниширование) и логнормальным за­коном — при преимущественном логнормальном распределении амплитуд гармоник (бесцентровое шлифование с поперечной подачей). В обоих слу­чаях функция плотности вероятности однозначно определена двумя пара­метрами — математическим ожиданием m и среднеквадратическим откло­нением а.

Рассчитанные первые четыре статистических момента (m, m2, m3, m4), среднеквадратическое отклонение а, показатели асимметрии а3 и экс­цесса а4 для распределения критерия К для бесцентрового шлифования и суперфиниширования приведены в табл. 6.2. Параметр наладки станка а имеет тот же смысл, что и ранее.

Анализ табл. 6.2 показал, что все варианты характеризуются поло­
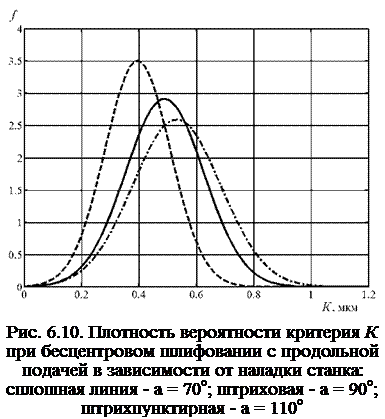
жительным показателем асимметрии и показателем эксцесса, равным трем и более. При бесцентровом шлифовании с продольной подачей наиболее нерациональный угол а = 110°, ему соответствует математическое ожида­ние погрешности базирования, равное 0,531 мкм, и среднеквадратическое отклонение 0,154 мкм. При наилучшем угле наладки а = 90° среднеариф­метическое и среднеквадратическое отклонения уменьшаются на 26 %.

При бесцентровом шлифовании с поперечной подачей наиболее не­рациональный угол а = 50°, при котором математическое ожидание по­грешности базирования равно 0,46 мкм и среднеквадратическое отклоне­ние 0,267 мкм. При наилучшем угле наладки а = 80° среднеарифметиче­ское отклонение уменьшается на 21 % и среднеквадратическое отклонение — на 15 %.

Таблица 6.2

Начальные моменты распределения критерия К в партии заготовок а т1 m2 а m3 аэ т4 а4 Бесцент овое шлиф ование с п родольной подачей 70 0,489 0,019 0,137 0,003 1,210 0,001 3,854 90 0,395 0,013 0,114 0,002 1,111 0,001 4,433 110 0,531 0,024 0,154 0,003 0,909 0,002 3,736 Бесцент овое шлиф )ование с поперечной подачей 50 0,460 0,072 0,267 0,022 1,148 0,024 4,714 80 0,365 0,051 0,227 0,015 1,291 0,016 5,872 110 0,403 0,067 0,258 0,024 1,404 0,025 5,730 Бесцентровое суперфиниширование 15 1,400 0,123 0,351 0,012 0,277 0,043 2,858 30 0,809 0,049 0,221 0,004 0,007 0,393 2,790 45 0,603 0,020 0,141 0,001 0,001 0,306 3,154

При бесцентровом суперфинишировании наиболее нерациональный угол а =15° (математическое ожидание погрешности базирования равно 1,4 мкм и среднеквадратическое отклонение 0,351 мкм). При наилучшем угле наладки а = 45° среднеарифметическое отклонение уменьшается примерно в 2,3 раза и среднеквадратическое отклонение — в 2,5 раза. Столь большие различия статистических оценок критерия К по сравнению с бес­центровым шлифованием объясняются тем, что оптимальный вариант наладки находится вне исследуемого диапазона угла а = 15… 45°.

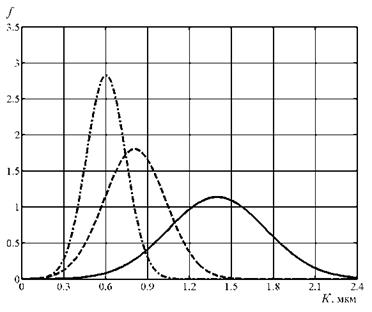
Графики плотности вероятности f для трех рассчитанных вариантов наладки изображены на рис. 6.10 — 6.12 соответственно. Критерий К рас­пределен при бесцентровом шлифовании с продольной подачей и супер­финишировании по нормальному закону, а при шлифовании с поперечной подачей — по логнормальному закону.

Сравнение оценок математического ожидания для критерия базиро­вания с величиной отклонения от круглости показало, что оптимальные варианты наладки шлифовального и суперфинишного станков способ­ствуют активному исправлению профиля поперечного сечения. Кроме то­го, наименьшему математическому ожиданию также соответствует наименьшее среднеквадратическое отклонение.

/

Рис. 6.12. Плотность вероятности критерия К при бесцентровом суперфинишировании в зависимости от наладки станка: сплошная линия — а = 15°; штриховая — а = 30°; штрихпунктирная — а = 45°

Проведенные исследования позволяют сделать вывод о том, что бес­центровые шлифовальные и суперфинишные станки целесообразно нала­живать на обработку определенных партий заготовок со стохастическими отклонениями формы по критерию точности микробазирования с исполь­зованием статистического моделирования Монте-Карло.