Формообразование поперечного сечения деталей при бесцентровом суперфинишировании

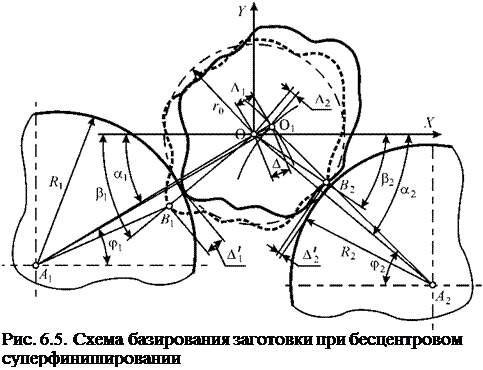
При бесцентровом суперфинишировании заготовка базируется на двух валках, поперечные сечения которых представляют собой окружно­сти радиусов R1 и R2 с центрами в точках А1 и А2 (рис. 6.5). Положение этих окружностей относительно начала системы координат(Х О Y) задано угла­ми ai и a2.

Считаем, что при базировании заготовка, описанная уравнением (6.1), стремится занять устойчивое положение на двух валках. При этом за­готовка смещается от номинального положения, последовательно перека­тываясь по поверхностям валков.

Установим точки контакта (так же, как и ранее для бесцентрового шлифования) на основе максимума зазора, выраженного модулем А’ и по­лярным углом Р:

А'(р1) = {r(р1 + ш0) — Гі(р1)} ^ max; А2 (р2 ) = {r(3600 — р2 ) — r2 (р2 )} ^ max’

где r1, r2 — уравнения окружностей левого и правого валков, определяемые по выражению, аналогичному (6.8).

Проекцию А1 смещения А’ на направление угла a1 находим из тре­угольника OA1B1 по теореме косинусов:

(R1 — А1)2 = r12 + (R1 + ro / — 2r1 (R1 + r1)cos(p1 — a1) ,

откуда после преобразований

Ai = R-Vп + (R1 + r0/ -2ri(Ri + r)cos(Р, — а,) . (6.13)

Аналогично находим проекцию А2 смещения Л’ на направление угла а2 из треугольника OA2B2:

А = R -^r22 + (R + r0)2 -2r2(R + r2)cos(fi2 — а2) . (6.14)

После базирования центр заготовки сместится в точку O1 и расстоя­ние от него до центра левого валка будет равно А1О1 = R1 + r0 + А,, а до центра правого валка А2О1 = R2 + r0 + Л2. Центр заготовки последовательно движется по левому валку по дуге окружности радиуса A, O, и по правому валку по дуге окружности радиуса A2O,. Пересечение этих траекторий и будет новым положением центра заготовки O1. Определим координаты точки O1 из совместного решения уравнений данных окружностей в про­екциях на оси X и Y:

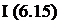-(R + r0)cosа + (R + r0 + A)cosф = (R + r0)cosа2 -(R + r0 + Л2)cosф;

— (R + r0)sin а + (R + r0 + A )sin ф = -(R + r0)sin а2 + (R + r0 + A )sin ф,

где ф1 и ф2 — углы наклона векторов A1O1 и A2O, к оси X (см. рис. 6.5).

В уравнениях (6.15) первые слагаемые в левой и правой частях пред­ставляют собой проекции центров окружностей валков, а вторые слагае­мые — проекции радиусов траекторий центра заготовки.

Решение системы уравнений (6.15) дает выражения для расчёта по­грешности базирования:

(6.16)

где a = (R + r)cos а2 + (R + r0)cos а; b = (R + r0)sinа2 — (R + r0)sinа;

c _ (R2 + ro + A2 / — (q2 + b) — (R1 + ro + A1 f 2(R1 + ro + A1)

Исследуем траектории движения центра заготовки при ее вращении в зависимости от наладки бесцентрового суперфинишного станка. В табл. 6.4 приведены расчетные траектории центра при одном обороте заготовки со средним радиусом r0 = 8 мм, имеющей отклонение формы в виде 2-, 3-, 4- и 5-й гармоник с амплитудами а2 = а3 = а4 = а5 = 1 мм. В качестве опти­мизируемого параметра выступает суммарный угол установки валков а. Радиусы валков приняты R1 = R2 = 62,5 мм и положение их центров А1 и А2 определено через параметры а1, а2 и r0. Так же, как и ранее, начальные фа­зы гармоник взяты равными нулю и углы установки валков приняты рав­ными а1 = а2.

Для 2-, 3-, 4- и 5-й гармоник рассчитан критерий К точности базиро­вания в зависимости от наладочных углов валков. Результаты расчета представлены в табл. 6.5. Для 2-й гармоники при углах а = 10, 15° и для 3-й гармоники при угле а = 10° имеет место провал заготовки между валками в ряде положений при ее вращении. Поэтому критерий К для указанных случаев не вычислен.

Траектории движения центра при бесцентровом суперфиниширова­нии похожи на траектории, полученные при бесцентровом шлифовании. Это объясняется тем, что радиусы валков многократно превышают откло­нения формы заготовки.

Исследование критерия К показало, что для 2-, 3-, 4-, 5-й гармоник оптимальным углом наладки в диапазоне а = 10 — 60° является максималь­ное значение 60°. Для приведенных примеров при а = 10 — 60° значение критерия К изменяется от 1,0 до 4,5. По аналогии с бесцентровым шлифо­ванием с поперечной подачей, можно предположить, что оптимальные уг­лы наладки располагаются в пределах а = 80 — 110°, однако реализация та­ких углов на суперфинишном станке невозможна по силовым ограничени­ям. Для рассчитанного диапазона наладок критерий К принимает значения только больше единицы, что говорит о копировании погрешностей базовой поверхности и наличии тенденции к созданию новых погрешностей. При уменьшении отношения радиусов валков и заготовки наблюдается некото­рое уменьшение критерия К. Однако, как будет показано далее, участие в процессе формообразования шлифовального бруска с большой площадью охвата поверхности заготовки создает условия для эффективного исправ­ления погрешностей формы.

Таблица 6.5

Критерий К при бесцентровом суперфинишировании n Угол наладки а, градус 10 15 20 25 30 35 40 45 50 55 60 2 — — 3,54 2,67 2,19 1,83 1,56 1,36 1,20 1,09 1,00 3 2,41 1,92 1,81 1,79 1,76 1,69 1,61 1,52 1,43 1,32 1,23 4 — 3,27 2,38 1,86 1,61 1,43 1,30 1,20 1,12 1,06 1,01 5 4,50 3,44 2,77 2,32 2,08 1,90 1,65 1,45 1,31 1,23 1,16

Помимо математической модели базирования, также разработана модель формообразования поперечного сечения заготовок при бесцентро­вом суперфинишировании [51, 52]. Предложенный подход основан на мо­делировании процесса съема припуска с учетом погрешностей базирова­ния и изменения натягов в технологической системе. В качестве обобщен­ного критерия формообразования выступает коэффициент К1 исправления профиля, равный отношению исходного А отклонения от круглости к по­лученному после обработки А1.

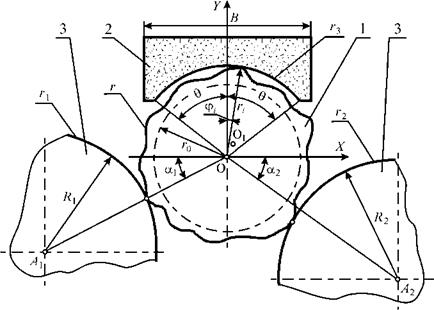
Расчетная схема формообразования представлена на рис. 6.6. Заго­товка 1 базируется на двух валках 3. Брусок 2 в приработанном состоянии имеет образующую в виде дуги окружности радиуса r3 с углом охвата 20. Значение угла 0 зависит от соотношения ширины бруска, диаметра заго­товки и величины приработки шлифовального бруска. Радиус r3 в процессе обработки меняется в пределах половины поля допуска на диаметр заго­товки. В рамках предложенной модели это не имеет принципиального зна­чения, поэтому радиус образующей бруска принят постоянным.

Поперечное сечение заготовки опишем следующим образом:

Р

Г = Г0 + t + Z anCOS(n^~^n) ,

n=2

где t — припуск на сторону.

Рис. 6.6. Схема формообразования заготовки при бесцентровом суперфинишировании

В процессе обработки стабилизируются натяги в ТС, созданные ис­ходными отклонениями формы детали и погрешностями базирования. При определении мгновенных натягов и мгновенных съемов металла приняты следующие допущения. Изменение радиуса заготовки по отношению к но­минальному вызывает изменение натягов в ТС и соответственно давления шлифовального бруска. При постоянной жесткости резания приращение давления прямо пропорционально приращению снимаемого металла.

Радиальный съем металла 8 в пределах длины контакта заготовки со шлифовальным бруском:

8 = г — (r0 +t—) + %Аг, m

где j — текущий оборот детали (1 < к < m); m — число оборотов детали, не­обходимое для съема припуска t; % — коэффициент, связанный с жестко­стью резания.

При расчете величины 8 учитывают только положительные значе­ния, при отрицательных значениях полагают 8 = 0. За j-й оборот детали в каждой точке профиля съем металла произойдет только один раз. Съем полного припуска t совершится за m оборотов заготовки.

При каждом текущем обороте детали 2jn получаем новый профиль г—, для которого заново рассчитываем погрешности базирования. После изме­нения угла ф до 2mn заготовку считают обработанной. Окончательный съем металла произойдет на величину, большую, чем исходный припуск t. Это объясняется дополнительным съемом металла из-за изменения натягов в ТС. Исходными данными при моделировании являются: радиус детали г0; параметры профиля п; ап и фп; припуск t; максимальное число m оборо­тов заготовки при обработке; радиусы валков R1 и R2; ширина В шлифо­вального бруска; углы контакта а і и а2.

Получив дискретно заданный профиль детали после расчетной обра­ботки, требуется найти его аналитический эквивалент и определить откло­нение от круглости. Если считать, что центры средней окружности детали до и после обработки совпадают с достаточной точностью, то параметры уравнения профиля в виде тригонометрического полинома (6.1) определя­ют по формулам Бесселя [53], а отклонение от круглости Д1 рассчитывают по стандартной методике. В случае, когда полученное значение К1 меньше требуемого [К1], проводят параметрическую оптимизацию при наличии ограничений. Единообразное математическое представление профиля де­тали при формообразовании и измерении позволяет проанализировать не только комплексный показатель К1, но и изменение амплитудного состава погрешностей.

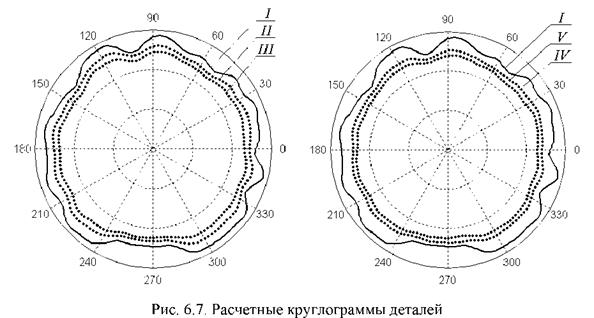
Рассмотрим пример моделирования процесса формообразования при следующих параметрах: r0 = 12 мм; t = 0,004 мм; m = 50; R1 = R2 = 60 мм; B = = 2 мм; а1 є [35°; 15°]; а2 є [15°; 35°]. Результаты представлены на рис. 6.7 в виде поперечных профилей детали: I — исходный; II — после обработки при указанных параметрах; III — после обработки с оптимальными углами контакта (а1 = 22°; а2 = 54°); IV — после обработки с увеличенным припус­ком (t = 0,008 мм); V — после обработки с увеличенной шириной бруска (B = = 24 мм). Профили изображены в виде наложенных друг на друга кругло — грамм с совмещенными центрами, одинаковым радиальным масштабом увеличения и различными средними радиусами записи (для равномерного размещения профилей в зоне записи диаграммы). Амплитуды гармониче­ских погрешностей детали для вариантов I и II представлены на рис. 6.8.

а б

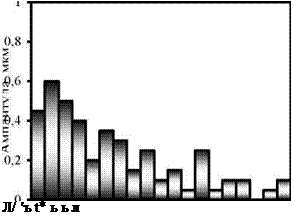
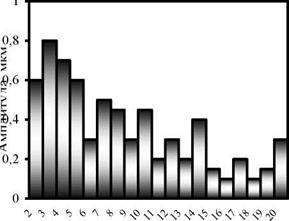
Рис. 6.8. Амплитудный состав гармонических погрешностей профиля детали:
а — вариант I на рис. 6.7; б — вариант II на рис. 6.7

Исходное отклонение от круглости детали составило А = 4,2 мкм. Для вариантов II — V отклонения от круглости Аі равно 3,1; 2,2; 1,8; 1,7 мкм, коэффициент К1 исправления профиля равен 1,35; 1,91; 2,33; 2,47 со­ответственно. Таким образом, увеличению критерия формообразования К1 способствуют: увеличение ширины инструмента, припуска на обработку, а также оптимизация наладочных параметров станка.

Результаты моделирования показали, что наибольшее влияние на ис­правление профиля заготовки оказывают ширина шлифовального бруска и припуск на обработку. Однако наличие жестких технологических ограни­чений приводит к необходимости поиска других параметров оптимизации. Поэтому наиболее актуальными параметрами при оптимизации процесса формообразования следует считать углы контакта заготовки с валками. По итогам моделирования рекомендована область оптимальных углов контак­та, определяемая соотношениями: а1 < а2 + 5°; а1 > 15°; а1 + а2 < 90°, по­

лучившая применение в разработке нового способа суперфиниширования [54].

Сравнивая результаты моделирования формообразования с результа­тами моделирования базирования, можно сделать вывод о том, что такие факторы, как большой угол охвата заготовки шлифовальным бруском и переменные углы контакта заготовки с валками, способствуют более эф­фективному исправлению погрешности формы.