Формообразование поперечного сечения деталей при бесцентровом шлифовании с поперечной подачей

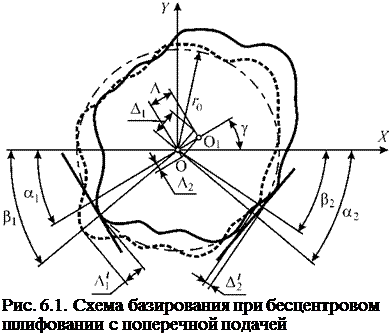
При бесцентровом шлифовании с поперечной подачей заготовка ба­зируется на двух, обычно плоских опорах. Базирование осуществляется по наружной или внутренней поверхности заготовки, независимо от того, ка­кая поверхность обрабатывается. Рассмотрим формообразование попереч­ного сечения заготовки на примере базирования по наружной поверхности. Положение базирующих элементов в основной системе координат (X O Y) определено радиусом заготовки r0 и наладочными углами аь а2 плоских опор (рис. 6.1). Дополнительная система координат (X1 Oi Yi) связана с центром O1 сечения заготовки после базирования и задана относительно системы (X O Y) радиус-вектором с модулем А и полярным углом у.

Определим погрешность базирования согласно изложенному подхо­ду. Уравнение профиля заготовки описано выражением (6.1). Уравнение прямолинейной опоры в полярной системе координат:

где X — угол, задающий перпендикуляр к опоре (Х1 = 180° + а1; Х2 = 360° — — а2).

Найдем точки контакта заготовки с опорами, установив ее в требуе­мое положение. Очевидно, что это будут те точки на профиле заготовки, которые наиболее близко расположены к опоре. Определим зазор между опорой и заготовкой в исходном положении, выраженный величиной А’ и полярным углом Р, на основе процедуры минимизации:

A’= {r — r} ^ max. (6.4)

В выражении (6.4) индексы, относящиеся к правой и левой опоре, для упрощения опущены. Величина A’ может принимать как положитель­ное, так и отрицательное значение.

Считаем, что заготовка одновременно и постоянно находится в то­чечном контакте с обеими опорами. Поэтому при базировании она должна последовательно перемещаться по опорам на величины Ai и A2, которые представляют собой проекции Д’ и Д’ на углы а2 и а1 противолежащих опор. Выражения для проекций определим из соотношений:

[A = A'[sin( Pj +а2) + cos( ^ +а2 )ctg( а +а2 )}•

( Д2 = Д2 [sin(р2 + а1) + COs(р2 + а1 )ctg(а1 + а2 Л

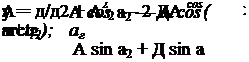Окончательно положение центра О1 заготовки после смещения по опорам находим векторным сложением смещений А1 и A2. Радиус-вектор центра О1 заготовки определим по формуле:

Для оценки погрешности представленной математической модели воспользуемся решением обратной задачи — повторным расчетом величин зазора между заготовкой и опорами по зависимости (6.4) после базирова­ния с использованием формул (6.1), (6.3) — (6.6). Относительная погреш­ность расчета представляет собой отношение зазора, полученного после расчетного базирования, к величине отклонения от круглости заготовки. Для рассмотренной модели расчетная погрешность не превышает 0,5 %.

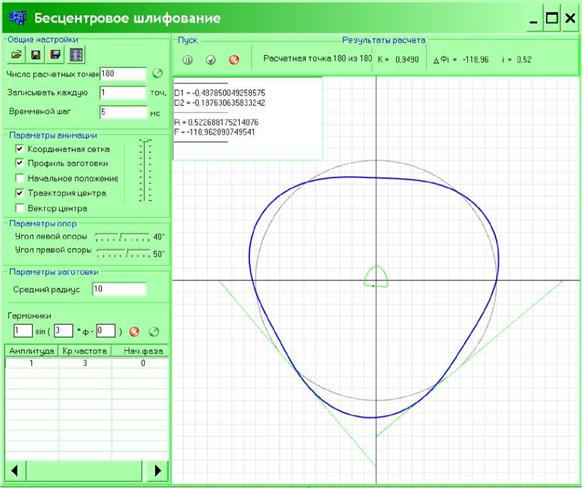
Методика расчета бесцентрового базирования реализована в виде программы на языке C++ Builder. На рис. 6.2 приведен интерфейс про­граммы, которая позволяет определить все параметры по формулам (6.1) — (6.6) в пошаговом режиме с полной визуализацией, а также анимировать процесс базирования. Для удобства пользователя профиль заготовки и наладочные углы опор задаются в интерактивном режиме. Предусмотрена возможность сохранения и загрузки сохраненных профилей заготовки (ес­ли используется реальный профиль с большим числом гармоник). В каче­стве основного результата расчета выводится значение критерия К.

При анализе бесцентрового базирования наибольший интерес пред­ставляет траектория движения центра заготовки при ее вращении. Траек­тория движения каждой точки на профиле заготовки будет кривой, конгру­энтной траектории центра с учетом ее радиуса. Таким образом, именно траектория центра заготовки определяет форму и величину отклонения профиля поперечного сечения после бесцентрового шлифования с попе­речной подачей.

Рис. 6.2. Интерфейс программы для расчета базирования при бесцентровом шлифовании с поперечной подачей

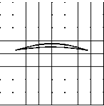
В табл. 6.1 даны примеры расчетной траектории центра заготовки, имеющей отклонение формы в виде 2-, 3-, 4- и 5-й гармоник, при одном обороте в зависимости от наладочных углов опор. В качестве переменного параметра выступает суммарный угол наладки а = аі + а2, так как отдель­ные значения а1 и а2 влияют только на начало отсчета полярного угла при вращении заготовки. В силу периодичности отклонений формы, получен­ные траектории за один оборот повторяются число раз, равное номеру рас­сматриваемой гармоники. Приведенные траектории симметричны относи­тельно вертикальной оси Y в связи с тем, что начальные фазы гармоник взяты равными нулю и углы опор приняты равными а1 = а2.

Для 2-, 3-, 4- и 5-й гармоник также рассчитан критерий К точности базирования в зависимости от наладочных углов опор. Результаты расчета представлены в табл. 6.2 для числа точек на траектории к = 180. Анализ показал, что увеличение числа точек на траектории с 36 до 180 приводит к уточнению величины К в пределах 0,5 %, а дальнейшее увеличение числа точек влияет на точность расчета К только в пределах 0,01 % от значения амплитуды соответствующей гармоники.

Таблица 6.1

Траектории движения центра заготовки при бесцентровом шлифовании

Таблица 6.2 Критерий К при бесцентровом шлифовании с поперечной подачей n Угол наладки а, градус 40 50 60 70 80 90 100 110 120 130 140 150 2 1,55 1,19 0,99 0,88 0,86 0,91 0,99 1,10 1,20 1,30 1,38 1,45 3 1,64 1,43 1,22 1,07 0,99 0,95 0,96 1,05 1,20 1,36 1,55 1,74 4 1,27 1,10 1,00 0,97 0,93 0,82 0,83 0,89 1,02 1,22 1,45 1,73 5 1,70 1,30 1,14 1,05 0,97 0,89 0,81 0,72 0,82 1,00 1,25 1,57

Траектории движения центра при бесцентровом базировании при малых углах а имеют вытянутую по оси Y форму, а при больших углах — вытянутую по оси Х (при нулевой начальной фазе гармоники). При траек­тории в виде линии (2-я гармоника, а = 90°; 3-я гармоника, а = 60, 120°; 4-я гармоника, а = 90, 120°) центр заготовки дважды проходит данную траек­торию.

При большинстве наладок преобладают траектории овальной и трех­гранной форм, что и обусловливает появление таких погрешностей на за­готовке после бесцентрового шлифования. Указанные кривые при гармо­ническом анализе представляют собой спектр гармоник, а овальность лишь в первом приближении может ассоциироваться со 2-й гармоникой. Прове­денные численные эксперименты не выявили каких-либо закономерностей между траекторией и углами наладки опор при рассмотрении отдельных гармоник. Исследование точности базирования по критерию К установило, что для 2-, 3-, 4-, 5-й гармоник оптимальные углы наладки а находятся в интервале от 80 до 110°. Для приведенных примеров при а = 40 — 150° зна­чение критерия К изменяется от 0,72 до 1,74. Таким образом, оптимальная наладка позволяет уменьшить погрешность базирования по сравнению с исходной погрешностью базового профиля заготовки на 30 %, в то время как нерациональная наладка способствует увеличению данной погрешно­сти до 2 раз.

Проведенные эксперименты позволяют сделать следующие выводы:

• процесс базирования при бесцентровом шлифовании с поперечной по­дачей является управляемым — оптимальная наладка углов опор станка позволяет уменьшить погрешность базирования по сравнению с исход­ной погрешностью базового профиля заготовки;

• характерные формы траектории при вращении центра заготовки — овальная и трехгранная; признаком нерациональной наладки станка следует считать существенное доминирование амплитуды 2-й гармони­ки по сравнению с остальными гармониками;

• при неизвестных «априори» отклонениях формы заготовки для мини­мизации 2-, 3-, 4- и 5-й гармоник оптимальные углы наладки непо­движных опор необходимо назначать от 80 до 110°.

• бесцентровый шлифовальный станок целесообразно налаживать на конкретную партию заготовок с вероятностным законом распределения погрешностей формы, а задачу оптимизации углов опор решать на ос­нове статистического моделирования.