Бесцентровое шлифование с поперечной подачей нашло применение при обработке фасонных поверхностей вращения, которые не могут быть обработаны по схеме с продольной подачей. Наиболее прогрессивным методом следует считать шлифование на неподвижных опорах, которое в настоящее время практически вытеснило технологию шлифования в патронном зажиме [9, 21].
В методе шлифования на неподвижных опорах ведущий круг заменен неподвижной жесткой опорой, а вращение передается специальной планшайбой, к которой заготовка прижимается торцом. Планшайба крепится на шпинделе узла изделия станка. Заготовка скользит обрабатываемой поверхностью по двум неподвижным опорам, и поэтому точность вращения в радиальном направлении не зависит от биения шпинделя. Кроме того, заготовка при обработке не зажимается, а, следовательно, не деформируется. Благодаря этому бесцентровое шлифование на неподвижных опорах обеспечивает повышение точности по таким параметрам, как разностенность, овальность, огранка.
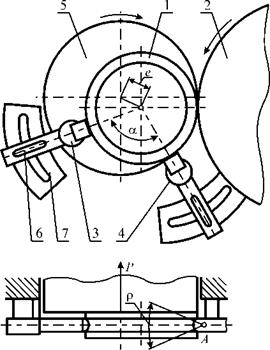
Бесцентровое наружное шлифование на неподвижных опорах имеет две разновидности: с базированием по обрабатываемой поверхности (способ «микроцентрик») и с базированием по обработанной внутренней поверхности (способ «концентрик»). На рис. 4.8 показана схема бесцентрового шлифования по способу «микроцентрик» с базированием заготовки по желобу на двух неподвижных опорах [21].
В схеме на рис. 4.8 желоб заготовки шлифуют методом качания. Заготовка 1 при обработке кругом 2 вместе со своим шпинделем качается вокруг точки А в пределах угла р. За счет этого движения достигается необходимая геометрия желоба. Заготовка опирается на две опоры 3 и 4, расположенные под углом а друг к другу и жестко закрепленные на вертикальной стойке, являющейся частью суппорта бабки изделия. Неподвижные опоры имеют круговое и радиальное наладочные перемещения относительно планшайбы 5 за счет кареток 6 и 7.
|
Рис. 4.8. Схема бесцентрового шлифования на неподвижных опорах [21] |
Заготовка прижимается к опорам в результате смещения ее оси вращения относительно оси вращения планшайбы. Для устойчивости в осевом направлении заготовка также прижимается к плоской поверхности планшайбы. Таким образом, радиальной базой служат неподвижные опоры, а осевой базой — планшайба. Планшайба жестко связана со шпинделем станка, прижим заготовки обычно осуществляют магнитным способом, который надежен и удобен в эксплуатации.
Силовое взаимодействие при бесцентровом шлифовании на неподвижных опорах рассмотрено в работе [21]. Однако в ней допущены две неточности: вместо попутного шлифования показано встречное шлифование, моменты сил рассмотрены не относительно мгновенного центра вращения, а относительно вертикальной оси. Отмеченные недостатки, а также скудность интерпретации полученных результатов снижают практическую ценность данной модели.
Рассмотрим схему сил, действующих в поперечном сечении заготовки при бесцентровом шлифовании на неподвижных опорах (рис. 4.9).
Уравнения равновесия заготовки в системе координат (X O Y):
XX = — PY — QsinХ + Nlcos( 180°-а-р)-N2sin(90°-р) + Rsin( 180°-а-р) +
+ R cos(90° — р) = 0;
XY = -р — G — Q cos Х + N sin( 180° — а — р) + N2 cos(90° — р) — R cos( 180° — а — р) + >
+ R sin(90° — р) = 0;
ХМ0 = (r + R — PZ )г0 = 0
где а — угол между неподвижными опорами; Р — угол установки опор относительно шлифовального круга; X — угол приложения силы Q (угол между осью Y и линией, соединяющей центр заготовки и центр планшайбы станка); Q — сила прижима заготовки; N, N2 — силы нормальной реакции опор; R1, R2 — силы трения заготовки с опорами.
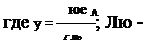проскальзывание между планшайбой и заготовкой.
Выразим силы трения через силы нормальной реакции и коэффициенты трения на неподвижных опорах. Считая коэффициенты трения на опорах равными, получим: R1 = fN; R2 = fN2. С учетом введенных обозначений и преобразований система уравнений (4.15) примет следующий вид:
N1 [ f sin( а + Р) — cos( а + Р)] + N2 [ f sin p — cos Р ] = PY + Qsin X;
N [sin(а + Р) + f cos(а + Р)] + N2 [sin Р + f cos Р] = kPY + G + Q cos X; > f(Ni + N2; = kPY.
Решим систему линейных уравнений, состоящую из двух первых уравнений (4.16), относительно неизвестных реакций опор N1, N2:
_ (kp + G + QcosX)[f sin(a + P)-cos(a + P)]-(PY + QsinX)[sin(a + P) + f cos(a + P)]
N N 1 ;
(sinP + f cosP)[f sin(a + P) — cos(a + P)]-(f sinP-cosP)[sin(a + P) + f cos(a + P)]
_ (P + QsinX)(sinP + f cosP) -(kp + G + Qcos X)(f sinP-cos P)
N2 •
_ (sin P + f cos P)[f sin(a + P) — cos(a + P)] — (f sin P — cos P)[sin(a + P) + f cos(a + P)]
(4.17)
Подставим выражения (4.17) в последнее уравнение системы (4.16):
[ f sin(a + P) — cos(a + P)][ f(G + Qcos X) + kp (f — a)] — [sin(a + P) + f cos(a + P)] x x [ fQ sin X + P( f — kb)] + af (P + Qsin X) — bf (kp + G + Qcos X) = 0, (4.18)
где a = sin P + f cos P; b = f sin P — cos P.
Уравнение (4.18) представляет собой условие равенства нулю суммарного момента от сил трения на опорах и силы резания. При его выполнении обеспечивается минимальная потребная мощность привода узла изделия. В случае отрицательного суммарного крутящего момента уменьшаются силы трения на опорах, что снижает их износ. Кроме того, с уменьшением трения в местах контакта заготовки с опорами улучшается качество базирующей поверхности, что важно при базировании по окончательно обработанной поверхности заготовки.
Для обеспечения стабильного прижима заготовки к обоим опорам можно дополнительно потребовать равенства сил реакций на опорах: N1 = N2; R1 = R2. В этом случае из (4.17) после преобразований получим:
(kp + G + Qcos X)(f sin( a + P) — cos( a + P) + f sin P — cos P) — (p +
+ Qsin X )(sin( a + P) + f cos( a + P) + sin P + f cos P) = 0. (4.19)
В уравнения (4.18) и (4.19) входят, с одной стороны, наладочные углы a, P и X, а с другой стороны, силы pY, G и Q. Выбор углов a и P осуществляют, исходя из минимальной погрешности базирования (см. п. 6.1). Радиальная составляющая силы шлифования для одной заготовки, по данным работы [21], колеблется в пределах 10 — 30 Н в зависимости от степени затупления шлифовального круга. Исследование силы Q в зависимости от величины эксцентриситета e и ее влияние на параметры точности обрабатываемых деталей показало, что сила Q изменяется в пределах 10 — 30 Н, а наилучшим значением является Q = 10 Н, при котором минимальны деформации заготовки и вибрации в процессе шлифования.
Таким образом, для оптимизации силовых параметров процесса по уравнениям (4.18) и (4.19) целесообразно использовать величину и направление силы Q при прочих равных условиях. Исследуем влияние указанных параметров на диапазон изменения углов a и P наладки шлифовального станка. Диаграммы допустимых значений углов a и P в зависимости от угла X и величины силы Q по условию (4.18) представлены на рис. 4.10 и 4.11, а по условию (4.19) — на рис. 4.12 и 4.13 соответственно. Для расчета приняты следующие исходные данные: G = 10 H; PY = 20 H; k = 0,5; f= = 0,17.
 |
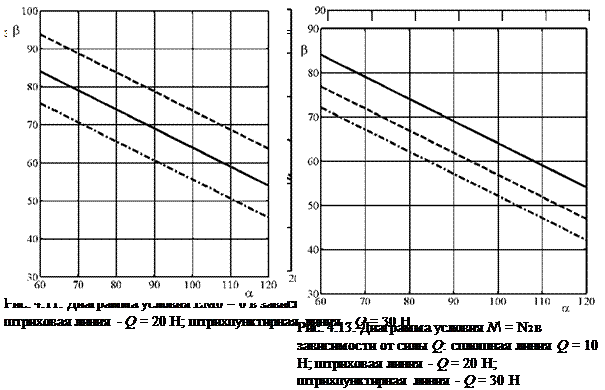Рис. 4.12. Диаграмма условия N = N2
в зависимости от угла X: сплошная
линия — X = 0; штриховая линия — X = 30О;
штрихпунктирная линия — X = -30о
Изменение коэффициентов трения f и шлифования к в уравнениях
(4.17) и (4.19) приводит к незначительному изменению абсолютных значений углов а и Р, но характер зависимостей, показанный на рис. 4.10 — 4.13, сохраняется.
Из рис. 4.10 — 4.13 видно, что все графики функций Р = f(a) имеют
вид монотонно убывающих кривых, а для условия N1 = N2 они близки к прямой линии. Изменению угла а от 60 до 120° соответствует изменение угла Р от 90 до 45°. Увеличение угла X способствует смещению графиков углов Р = f(a) в сторону больших значений при обоих условиях (4.18) и
(4.18) . Увеличение силы Q приводит к увеличению углов а и Р по условию (4.18) и уменьшению по условию (4.19).
Таким образом, общие рекомендации по установке углов а и Р следующие. Угол а назначают из условия минимальной погрешности базирования в зависимости от отклонений формы заготовок. Значение силы Q принимают минимально достаточным для стабильного прижима заготовки к опорам, угол ее приложения X может изменяться в достаточно широких пределах +45°. Равномерное распределение сил реакции на опорах и минимальный суммарный крутящий момент обеспечивают выбором угла Р при заданных остальных параметрах.