Один из наиболее сложных случаев при бесцентровом суперфинишировании — обработка бомбинированных поверхностей. Для создания
бомбинированной поверхности на заготовке формообразующая траектория должна быть дугой окружности определенного радиуса, согласованного по величине с радиусом бомбины. Традиционно обработку бомбинированных поверхностей осуществляют на суперфинишных станках с валковыми устройствами, включающими два валка со сложным профилем осевого сечения. Изготовление таких валков требует специализированных многокоординатных шлифовальных станков, из-за чего стоимость валкового устройства достигает 40 % от всего суперфинишного станка. Потребность подшипниковых заводов в данной продукции велика, однако их возможности не позволяют организовать производство подобных валков вследствие отсутствия необходимого оборудования. Поэтому актуальна разработка альтернативной технологии бесцентрового суперфиниширования с использованием валков простой геометрической формы.
В работе [31] исследовалась формообразующая траектория при бесцентровом суперфинишировании цилиндрических поверхностей и решалась задача по минимизации ее отклонений от прямолинейной. Анализ показал, что на суперфинишном станке с валками в виде однополостных гиперболоидов траектория движения цилиндрических заготовок приближенно соответствует дуге окружности в зависимости от геометрической наладки станка. Указанный факт стал основанием для изучения возможности обработки бомбинированных поверхностей на валках, имеющих форму однополостных гиперболоидов.
Установим формообразующую траекторию для цилиндрических заготовок на валках в виде однополостных гиперболоидов и оценим ее отклонение от дуги окружности, а также исследуем влияние параметров наладки на радиус дуги аппроксимирующей окружности. Для этого проведем численный эксперимент, в котором рассчитаем координаты формообразующей траектории по формулам (3.13), (3.14) для различных сочетаний размеров заготовки, валков и параметров наладки станка.
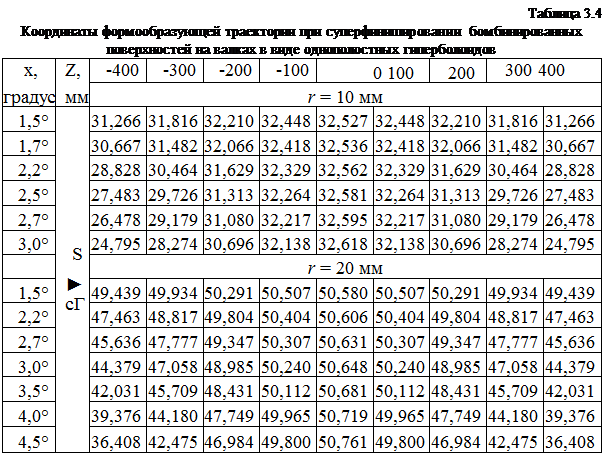
В табл. 3.4 представлены некоторые результаты численного эксперимента для следующих исходных данных: угол образующей однополостного гиперболоида у = 1°; минимальный радиус валка R = 60 мм, межосевое расстояние валков 2v = 124 мм. Исходно цилиндрические заготовки имеют радиусы r = 10, 20 мм. Точность решения системы (3.13) задана значением целевой функции Ф < 10-6, вычисляемой по выражению (3.14).
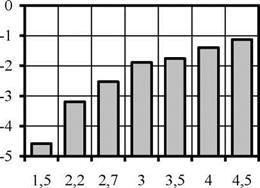
Аппроксимация полученных координат формообразующей траектории (рис. 3.6) проведена по трем точкам и методом наименьших квадратов. Для определения инвариантности наладочных параметров расчет выполнен для четырех длин валков (табл. 3.5). Также на рис. 3.7 показано изменение целевой функции Ф для заготовки r = 20 мм (для лучшего масштаба график построен в логарифмической системе координат).
 |
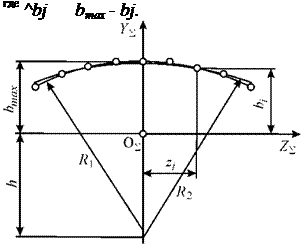
Радиус R1 аппроксимирующей дуги окружности по трём точкам рассчитан по формуле:
![]() М{ 2 + Z? 2ЛЬ; ’
М{ 2 + Z? 2ЛЬ; ’
|
|
 X, градус
X, градус
Рис. 3.6. Схема аппроксимации траектории Рис. 3.7. Изменение целевой функции
Радиус R2 аппроксимирующей дуги окружности методом наименьших квадратов найден на основе минимизации функционала F:
n I—————-
F = ^(bj-TjR2 ~ Z — h)2 ^ min,
i=1
где h — вертикальная координата центра дуги окружности.
|
Таблица 3.5 Радиусы аппроксимирующих окружностей формообразующей траектории при обработке бомбинированных поверхностей
|
Выявлено, что формообразующая траектория отличается от геометрически точной окружности, однако отклонения невелики. Расхождения между радиусами R и R2 при аппроксимации по трем точкам и методом наименьших квадратов находятся в пределах 0,5 %. Поэтому на практике расчет достаточно вести по трем точкам траектории. Погрешность аппроксимации монотонно увеличивается при уменьшении радиуса дуги (см. рис. 3.7). Максимальная погрешность аппроксимации соответствует наибольшей длине валков Z є [-400;400].
Анализ показал, что увеличение высоты b траектории в вертикальной плоскости приводит к уменьшению радиуса R2 аппроксимирующей окружности. При этом отклонения траектории от окружности также увеличиваются. Характерен рост кривизны формообразующей траектории по сравнению с кривизной аппроксимирующей окружности.
Оптимизацию наладочных параметров X и v суперфинишного станка, позволяющую получить заданную величину b и, как следствие, требуемый радиус R2 формообразующей траектории, можно выполнять как одновременно по обоим указанным параметрам, так и по каждому из них в отдельности. Увеличению высоты b при прочих равных условиях способствуют: увеличение угла перекрещивания осей и длины валков, радиуса заготовки, уменьшение межосевого расстояния валков. Угол перекрещивания осей валков всегда должен быть больше, чем угол образующей однополостного гиперболоида. Однако при значительном увеличении угла X возможна ситуация, когда заготовка располагается ниже точки перекрещивания валков и фактически обработка не возможна.
Рассмотрение валков различной длины при одной наладке станка показало, что полученные радиусы аппроксимирующей окружности во всех случаях близки. Например, для заготовки r = 10 мм отклонения находятся в пределах 2 %, а для заготовки r = 20 мм — в пределах 7 %. Таким образом, можно сделать вывод о том, что заданная наладка суперфинишного станка обеспечивает определенный радиус дуги окружности вне зависимости от длины валков.
При обработке бомбинированных поверхностей на валках в форме однополостных гиперболоидов затруднительно получение малых радиусов траектории движения и соответственно радиусов профиля заготовки. Результаты расчета наладок, обеспечивающих минимальные радиусы Rmin дуговой траектории при обработке заготовок различных диаметров, даны в табл. 3.6. Из табл. 3.6 видно, что с увеличением диаметра заготовок диапазон минимальных радиусов формообразующей траектории расширяется.
При наладке бесцентрового суперфинишного станка имеются конструктивные, геометрические, кинематические и силовые ограничения. Конструктивные ограничения накладываются на диаметры валков, межосевое расстояние и угол перекрещивания. Г еометрическая задача сводится к решению системы уравнений (3.13) с помощью минимизации функции (3.14). Очевидно, что при больших углах X на краях валков создается ситуация, когда заготовка для одновременного контакта с обоими валками должна повернуться в горизонтальной плоскости на значительный угол.
При этом нормали к поверхностям заготовки и валков не совпадают и, как результат, система уравнений (3.13) не имеет точного решения, что выражается в возрастании значения целевой функции (3.14), выходящей за допустимые пределы.
Таблица 3.6
|
Параметры наладки и формообразующей траектории при суперфинишировании бомбинированных поверхностей
|
Кинематические ограничения подразумевают обеспечение необходимых окружной и продольной скоростей заготовки, а также угла сетки рисок. Указанные кинематические параметры, с одной стороны, зависят от соотношения диаметров валков, заготовки, угла перекрещивания и межосевого расстояния валков, а, с другой стороны, регулируются скоростью вращения валков и частотой осцилляции шлифовальных брусков. Как правило, кинематические факторы не накладывают жестких ограничений на наладку суперфинишного станка.
Характерная особенность бесцентрового суперфиниширования — силовое замыкание контакта, обеспечивающее стабильное вращение заготовки. Решение данной задачи приведено в п. 4.3. Из него следует, что необходимо ограничивать максимальные значения углов контакта заготовки с валками. Указанные ограничения можно выразить через диапазон изменения межосевого расстояния и угла перекрещивания осей валков.
Общие рекомендации по наладке суперфинишного станка при обработке бомбинированных поверхностей можно сформулировать следующим образом. Вначале выбирают минимальное межосевое расстояние валков, удовлетворяющее условию силового замыкания контакта. Затем устанавливают угол перекрещивания осей валков, ограниченный решением геометрической задачи и конструктивными особенностями станка. В последнюю очередь назначают скорость вращения валков и частоту осцилляции шлифовальных брусков станка.