Наладка бесцентровых суперфинишных станков при обработке цилиндрических поверхностей

В условиях многономенклатурного производства (например, в под­шипниковой промышленности), станок с одним и тем же валковым устройством используют для обработки цилиндрических деталей различ­ных диаметров d. При этом за номинальный диаметр dН детали при профи­лировании валков обычно принимают среднее значение из диапазона об­работки [19].

Анализ формообразующей траектории показал, что при постоянных валках при обработке заготовок различных диаметров имеют место откло­нения, величина которых во много раз превосходит допуск на диаметр де­тали [18]. Поэтому необходима минимизация данных отклонений за счет подналадки суперфинишного станка. Известная методика [19], основанная на обобщении экспериментальных результатов, позволяет установить ка­чественный характер влияния параметров наладки, но не может обеспе­чить высокой точности расчета. Строгое решение указанной задачи воз­можно только в рамках новой модели, представленной уравнениями (3.13).

Вначале установим характер погрешностей, возникающих при обра­ботке заготовок с диаметром, отличным от расчетного при профилирова­нии валков. На практике используют несколько типов валков. Несмотря на то, что не все из них удовлетворяют принципу взаимного огибания по­верхностей, в ряде случаев их применение рационально по двум причинам. Во-первых, валки в виде однополостных гиперболоидов имеют простую геометрическую форму (что, однако не гарантирует простоту изготовления методом шлифования) и меньшие габаритные размеры по сравнению с другими. Во-вторых, целесообразность применения того или иного типа валков для обработки широкого диапазона размеров заготовок оконча­тельно не получила теоретического обоснования.

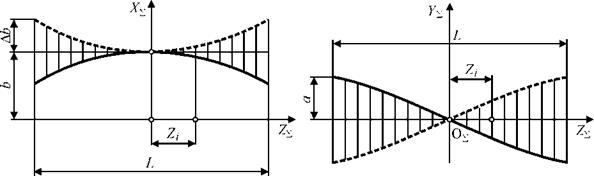
Рассмотрим следующие типы валков для обработки цилиндрических поверхностей: а — однополостный гиперболоид (станки фирмы Mikrosa); б — близкий к гиперболоиду с симметричным профилем [34]; в — близкий к ги­перболоиду с несимметричным профилем [19] (отечественные станки); г — квазигиперболоид [35]. Указанные типы валков при анализе были разделе­ны на две группы: с симметричным профилем (а, б) и с несимметричным профилем (в, г). Характер отклонений формообразующей траектории в проекциях на вертикальную и горизонтальную плоскости станка показан на рис. 3.5, где для несимметричных валков сплошной линией изображены отклонения для обрабатываемого диаметра больше номинального, и штри­ховой линией — для диаметра меньше номинального. У симметричных вал­ков показаны: сплошная линия — для обрабатываемого диаметра меньше номинального и штриховая линия — для диаметра больше номинального.

Отклонения формообразующей траектории в горизонтальной Да и в вертикальной ДЬ плоскостях, представляют собой максимальную разность номинальных и расчетных значений параметров а и Ь соответственно. При этом отклонение ДЬ = bmax — bmin, отклонение Да = а, так как номинальное значение а равно нулю.

Установлено, что если диаметр заготовки меньше номинального d < dH, то траектория при симметричных валках имеет вогнутый вид, а при несимметричных — выпуклый вид. Если диаметр заготовки больше номи­нального d > dH, то при симметричных валках траектория выпуклая, а при несимметричных — вогнутая. Отклонения траектории в вертикальной плос­кости симметричны относительно плоскости Zj = 0. Отклонения траекто­рии в горизонтальной плоскости с достаточной точностью аппроксимиру­ются прямой, симметричной относительно точки Об-

Отклонения в вертикальной плоскости непосредственно определяют профиль продольного сечения деталей, а отклонения в горизонтальной плоскости, не выходящие за ширину инструмента, мало сказываются на точности обработки. Таким образом, в первую очередь требуется миними­зация отклонений формообразующей траектории в вертикальной плоско­сти.

В общем случае задачу оптимизации наладочных параметров X и v суперфинишного станка решают с помощью минимизации целевой функ­ции G, которую находят по алгоритму как разность максимальных и ми­нимальных отклонений формообразующей траектории в вертикальной плоскости при минимальных отклонениях в горизонтальной плоскости:

G(фХ, у) = {Ътах — bmm} lm(a}^ min, (3.15)

где Ф — целевая функция, определяемая по выражению (3.14).

Выявлено, что отклонения формообразующей траектории в верти­кальной плоскости в большинстве случаев удается минимизировать до требуемой величины. Однако отклонения в горизонтальной плоскости в меньшей степени поддаются управлению, а в ряде случаев минимизация отклонения в вертикальной плоскости приводит к увеличению отклонений в горизонтальной плоскости. Поэтому необходима коррекция положения шлифовальных брусков относительно траектории движения заготовок. Учитывая, что отклонения в горизонтальной плоскости близки к прямоли­нейным, предложен способ наладки станка, при котором валковое устрой­ство разворачивают относительно каретки суперфинишного станка [36].

Проведенные эксперименты по оптимизации формообразующей тра­ектории позволяют сделать следующие выводы:

• оптимальная наладка суперфинишного станка обеспечивает минимиза­цию отклонений формообразующей траектории для деталей: d < dH при увеличении X или уменьшении v (симметричные валки) и при умень­шении X и v (несимметричные валки); d > dH — при уменьшении X или увеличении v (симметричные валки), при увеличении X или уменьше­нии v (несимметричные валки);

• для несимметричных валков при оптимизации параметра v для вариан­та d < dH не удается снизить отклонения в вертикальной плоскости до требуемой величины;

• отклонения формообразующей траектории в горизонтальной плоскости при оптимизации снижаются незначительно, поэтому необходима кор­рекция относительного положения валкового устройства и суперфи­нишных станций станка;

• при соотношении диаметров d и dH, различающемся более чем в пять раз, не удается минимизировать отклонения формообразующей траек­тории при конструктивно реализуемых наладках станка, что определя­ет диапазон применимости метода подналадок;

• рекомендуемая точность геометрической наладки бесцентрового су­перфинишного станка составляет: по углу перекрещивания — AX = 10", по межосевому расстоянию — Av = 0,2 мм.