3.1. Математическая модель для расчета формообразующей траектории при бесцентровом суперфинишировании
При бесцентровом суперфинишировании точность формообразующей траектории непосредственно определяет точность поверхности и отклонения профиля продольного сечения заготовок. Так, для формообразования цилиндрической поверхности необходима прямолинейная траектория, параллельная направлению осцилляции шлифовальных брусков, а для бомбинированной поверхности — дуговая траектория с радиусом, согласованным по величине с радиусом профиля детали.
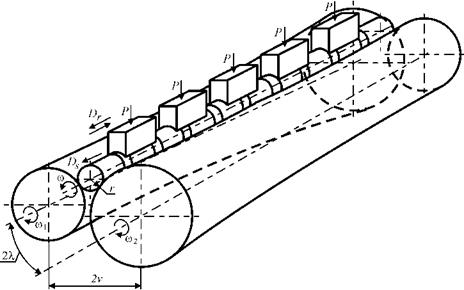
Валковое устройство суперфинишного станка предназначено для одновременного базирования и создания движения подачи, что достигается пространственным перекрещиванием осей двух валков. Формообразующая траектория зависит от геометрии валков и параметров наладки — угла перекрещивания 2Х и межосевого расстояния 2v (рис. 3.1).
|
Рис. 3.1. Схема бесцентрового суперфиниширования |
Расчет наладочных параметров проводят, во-первых, при проектировании валкового устройства для определения оптимальных геометрических, а затем кинематических и силовых параметров процесса. Во-вторых, при подналадке станка при использовании одного и того же валкового устройства для обработки цилиндрических заготовок различных размеров. В-третьих, необходимость подналадки возникает в случае эксплуатации валков с геометрией, не соответствующей теоретической, вследствие тех
нологических трудностей их изготовления (например, при обработке бом- бинированных поверхностей).
Задача геометрической наладки валкового устройства впервые получила теоретическое решение в работе [30]. Однако указанная математическая модель для расчета формообразующей траектории построена без возможности поворота заготовки. Такое допущение приемлемо для анализа прямолинейной траектории, а методика хорошо зарекомендовала себя при наладке станка на обработку цилиндрической поверхности [31]. В случае непрямолинейной траектории движения, требующейся при изготовлении поверхностей со сложной образующей, подобный подход не обеспечивает необходимую точность.
Рассмотрим более строгую математическую модель, в которой заготовка представлена с учетом ее длины и положения в евклидовом пространстве, в общем случае заданного шестью координатами (тремя координатами центра и тремя поворотами вокруг осей декартовой системы координат). В условно неподвижной системе координат Ss станка вводят совокупность плоских сечений ZE = Z, в которых валки и заготовка находятся в дискретном контакте. Определение формообразующей траектории без нарушения общности сводится к установлению положений оси заготовки в сечениях при ее одновременном контакте с правым и левым валками.
Для решения контактной задачи используем основную теорему пространственных зацеплений. Для взаимно огибаемых поверхностей должно выполняться равенство радиус-векторов r и касательных т в контактных точках поверхностей в единой условно неподвижной системе координат. Аналитическим эквивалентом одновременного контакта заготовки с правым и левым валками является система векторных уравнений:
.
где г/, ГП — радиус-векторы точек контакта на поверхности заготовки с левым и правым валком; г/, гП — радиус-векторы точек контакта на поверхности левого и правого валка; тЛ, тП, тЛ, тП — нормированные касательные к точкам контакта на поверхности заготовки, левого и правого валка соответственно.
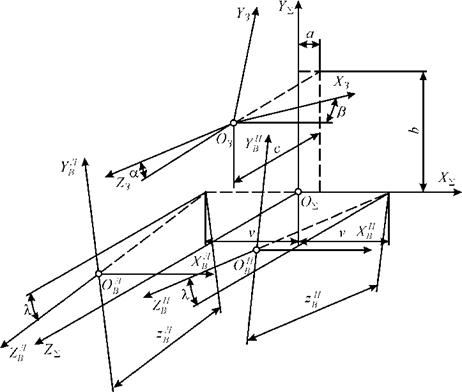
Формообразующую систему представим в виде совокупности следующих координатных систем (рис. 3.2): SE(XE Ое Ye Ze) — условно неподвижная система, связанная со станиной станка; S3(X3 ОЗ Y3 Z3) — система заготовки; SЛ (ХЛ ОЛ YЛЛ ZЛ) — система левого валка; SЛ (ХЛ ОЛ YЛ ZЛ) —
система правого валка. Система координат S3 относительно системы S2: повернута вокруг оси Х2 на угол а и смещена величину а, повернута вокруг оси 72 на угол Р и смещена на величину b, смещена по оси Z2 на величину С. Поворот системы S3 относительно системы S2 вокруг оси Z2 не введен, поскольку он определяет лишь начало отсчета криволинейной угловой координаты поверхности заготовки. Системы координат SЛ и SП относительно системы S2 смещены по осям ХЛ и zn на величины zЛ и zП, по
вернуты вокруг оси Х2 на угол X против и по часовой стрелке и смещены на величины — v и v соответственно.
|
Рис. 3.2. Координатная схема бесцентрового суперфинишного станка |
Валки представляют собой тела вращения, как правило, со сложным профилем осевого сечения, который находится для конкретных размеров заготовки и параметров наладки станка [18]. Поэтому при решении контактной задачи опишем валки как совокупность усеченных конусов, каждый из которых задан радиусом R основания, углом у образующей и координатой zB, отсчитываемой вдоль оси конуса. Радиус R основания конуса равен радиусу профиля валка, а угол у образующей — углу касательной к осевому профилю валка в сечении zB. Заготовка в большинстве случаев имеет исходно цилиндрическую поверхность.
Поверхность цилиндрической заготовки в векторно-параметрической форме в системе S3 опишем следующими уравнениями (рис. 3.3): левая сторона
правая сторона
rf = rcosQn • i — rsinQn • j + z^ • k, (3.3)
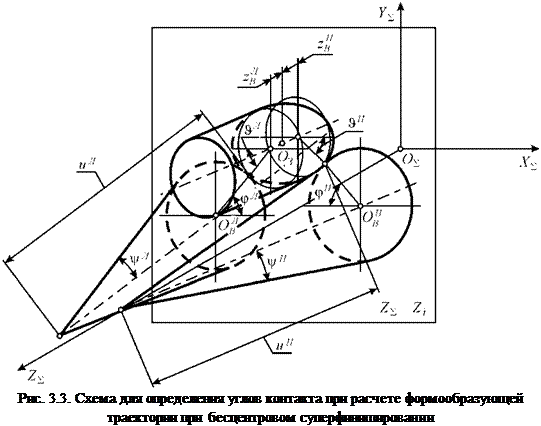 |
где r — радиус заготовки; &л, §n, zЛ, zf — угловая и линейная криволинейные координаты цилиндрической поверхности заготовки.
Поверхность валка, как поверхность конуса, в параметрическом виде опишем следующими уравнениями в системах SЛ и Sf соответственно: левый валок
Xл = ил sin ул cos фл;
![]()
![]() 7/ = ил sin фл sin фл;
7/ = ил sin фл sin фл;
Zл = R л ctgфл — и л cos фл,
правый валок
-ип sin фп cos фп;
= ип sin фп sin фп;
ZП = Rп ctg фп — ип cos фп, где Rл, R — радиусы оснований конусов; фл, фп, ил, ип — угловая и линей-
~ ~ л п
ная криволинейные координаты конической поверхности; ф, ф — углы
образующих конусов левого и правого валка соответственно.
Уравнения (3.2) и (3.3) заготовки при переходе в систему координат Ss преобразуют на основе формул:
Х^з = X3cosP + Z3 sin Р + a;
![]() YX3 = Y3cosa — (X3sinP — Z3 cos Р)sin a + b; > ZZ3 = — Y3sina — (X3sinP — Z3 cos Р) cos a + c.
YX3 = Y3cosa — (X3sinP — Z3 cos Р)sin a + b; > ZZ3 = — Y3sina — (X3sinP — Z3 cos Р) cos a + c.
В выражении (3.6) индексы, характеризующие правую или левую контактную сторону заготовки, для упрощения записи не указаны, так как преобразования идентичны.
Уравнения (3.4) и (3.5) валков при переходе в систему координат Ss преобразуют следующим образом: левый валок
ХЛ = Хлв — v;
![]()
![]() YBB = Yf cosX — (ZЛ + zЛ ) sin X; > Z Л = Y/ sinX + (Z Л + zB ) cos X;
YBB = Yf cosX — (ZЛ + zЛ ) sin X; > Z Л = Y/ sinX + (Z Л + zB ) cos X;
правый валок
XSB = ХВП + v;
Y"B = YП cosX + (Z П + z% ) sin X; >
Z П = — YП sinX + (Z П + z% ) cos X;
где 2X — угол перекрещивания осей валков; 2v — межосевое расстояние валков; z;Л, zП — координата, задающая осевое положение текущего конуса относительно точки OS перекрещивания осей валков.
Выражения для нормированных касательных к поверхностям в системе координат Ss имеют вид: левая сторона заготовки
х^ = — sin$B cosP л ;
тЗЛг = cosQB cos aB + sin §л sin aB sin Pл; (3.9)
x3z = — cosQB sin aл + sin&B cos aл sin Pл;
правая сторона заготовки
x^ = sin&n cosP n;
x^y = cos§n cos an — sin Qn sin an sin Pn; (3.10)
xTz = — cos&n sin an — sin&n cos an sin Pn;
левый валок
xBx = — cosV л sinq л;
хВЛ = cosvл cos фл cos X — sin vл sin X; (3.11)
хВЛ = cosvл cos фл sin X + sin vл cos X;
правый валок
В окончательном виде система уравнений (3.1) после подстановки в нее выражений (3.2) — (3.12) примет вид:
f = u sin у cos ф + rcos $ cos Р-z3 sin Р-v — a = 0;
f2 = u3 sin у3 sin ф3 cos К + Asin К + r sin $3 cos a + B sin a — b = 0;
f = u3 sin у3 sin ф3 sin К + Acos К-r sin $3 sin a-Bcos a-c = 0;
f4 = uп sin уп cos фп + rcos $п cos Р + zn sin Р — v + a = 0;
f = uп sin уп sin фп cos К — C sin К + r sin $п cos a + Dsin a — b = 0;
![]() f = uп sin уп sin фп sin К-Ccos К + r sin $п sin a + Dcos a + c = 0;
f = uп sin уп sin фп sin К-Ccos К + r sin $п sin a + Dcos a + c = 0;
f = sin $3 cos Р — cos у3 sin ф3 = 0;
f = cos $3 cos a + sin у3 sin a sin Р — cos у3 cos ф3 cos К + sin у3 sin К = 0; f = cos $3 sin a — sin у3 cos a sin Р + cos у3 cos ф3 sin К + sin у3 cos К = 0; f0 = sin $п cos Р — cos уп sin фп = 0;
fu = cos $п cos a — sin уп sin a sin Р — cos уп cos фп cos К — sin уп sin К = 0; fy-, = cos $п sin a + sin уп cos a sin Р — cos уп cos фп sin К + sin уп cos К = 0;
где A = R3^у3 — u3 cos у3 + z3 ; В = r cos $3 sin Р + zf cos Р;
C = Rпcg-у п — uп cos уп + zn; D = — r cos $п sin Р + гп cos Р.
Для решения системы трансцендентных уравнений (3.13) используем метод параметрической оптимизации, при котором находят минимум целевой функции Ф:
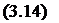
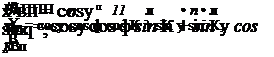 |
Ф($3 ,$п, z3 ,гп, ф3 ,фп, u3 ,uп. a^.a.^c) = ^f2 ^ min.
i=1
При решении системы (3.13) нужно учитывать следующие особенности, отмеченные в работе [32]. Задав плоское сечение (положив Z£ = Zi), уравнения f = 0 и f6 = 0 превращают в тождества (рассматриваемые отдельно для каждого из валков и заготовки), из которых выражают неизвестные параметры z3, гп, u3, ып и подставляют их в уравнения f1 = f2 = f3 = = f4 = 0, что позволяет сократить систему (3.13) до десяти трансцендентных уравнений. Координаты a, b, c определяют положение точки на оси заготовки, относительно которой она поворачивается на углы a и Р. Чтобы координаты a и b определялись именно в сечении Zs = Zi, следует положить параметр с = Zi. В результате число неизвестных параметров, подлежащих определению на основе оптимизации целевой функции Ф, сокращается с тринадцати до восьми.
Целевая функция Ф, представляющая собой сумму квадратов левых частей уравнений системы (3.13), является мультимодальной, что обуслов
лено периодичностью тригонометрических выражений, входящих в ее состав. Для поиска глобального экстремума целевой функции F использован метод мультистарта [29]. Для многомерной оптимизации применен метод Хука-Дживса, который относится к методам поиска нулевого порядка и выгодно отличается простотой и эффективностью. Условием окончания поиска служило уменьшение шага до определенной величины, что соответствовало заданной точности определения искомых параметров. Линейные параметры находились с точностью 10- , угловые параметры — с точ-
о
ностью 10- , при этом целевая функция в среднем принимала значения Ф = = 10- . Установлено, что в большинстве случаев можно локализовать глобальный минимум с помощью правильного выбора начального приближения. Таким начальным приближением служит решение системы уравнений (3.13) при угле X = 0. Использование данного приема позволяет избежать нахождения всех экстремумов мультимодальной целевой функции и существенно повысить эффективность решения.
В качестве примера рассчитаем формообразующую траекторию для трех типов валков, представленных в табл. 3.1. Теоретически точные валки для изготовления бомбинированной поверхности имеют идентичный симметричный профиль, валки для изготовления цилиндрической поверхности — одинаковый несимметричный профиль и развернуты в противоположных направлениях, в результате чего они симметричны относительно плоскости zB = 0.
Таблица 3.1
|
Профили валков суперфинишного станка для обработки цилиндрической и бомбинированной поверхностей
|
Координаты формообразующей траектории приведены в табл. 3.2 для следующих параметров: цилиндрическая поверхность — r = 15 мм, X = = 1,75°, v = 71 мм; бомбинированная поверхность — r = 10 мм, X = 1,5°, v = = 30 мм; бомбинированная поверхность, обрабатываемая на валках в форме однополостного гиперболоида — r = 15 мм, X = 4,125°, v = 66 мм.
Таблица 3.2
|
Расчетные координаты формообразующей траектории Обработка цилиндрической поверхности
|
Поверхности валков для обработки цилиндрических и бомбиниро — ванных поверхностей получены на основе строгого профилирования, поэтому они обеспечивают теоретическую траекторию с известными параметрами и используются как тестовые. Валки в форме однополостного гиперболоида для исходно цилиндрической заготовки создают траекторию, близкую к дуге окружности [33].
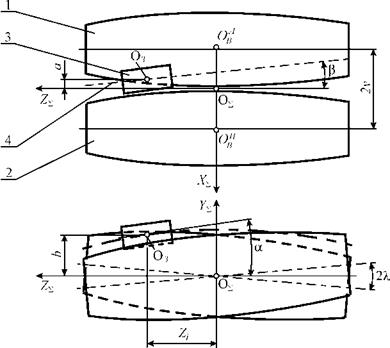
Наиболее актуальными параметрами для прямолинейной траектории при обработке цилиндрических поверхностей являются высота траектории Ьтах и отклонения в проекциях на вертикальную АЬ и горизонтальную Аа плоскости станка (рис. 3.4). Для дуговой траектории при обработке бомби — нированных поверхностей важны радиус траектории R0, вертикальное положение дуги, заданное координатой Ьтах и отклонения в горизонтальной плоскости Аа. На основе табл. 3.2 рассчитаны параметры формообразующих траекторий для новой модели, известной модели [30], а также фактические значениями параметров, которые приведены в табл. 3.3.
|
Рис. 3.4. Параметры пространственной формообразующей траектории: 1 — левый валок; 2 — правый валок; 3 — заготовка; 4 — формообразующая траектория |
|
Таблица 3.3 Параметры формообразующей траектории
|
Анализ табл. 3.3 показал, что новая математическая модель обеспечивает более высокую точность расчета формообразующей траектории, чем предшествующая. Так, для цилиндрической поверхности теоретическая высота траектории составляет bTmax = 31,068 мм, полученная по расчету bmax = 31,054 мм, а отклонения Ab и а не превышают 1 мкм. Для бомби- нированной поверхности теоретические радиус дуги окружности RT0 = 500 мм и высота bTmax = 25 мм, полученные по расчету R0 = 488 мм, bmax = 24,983 мм. Рассчитанные значения углов поворота заготовки в вертикальной и горизонтальной плоскости соответствуют форме траектории (ось заготовки приближенно является касательной к траектории).
Один из наиболее значимых выводов, определяющих практическую ценность разработанной модели, — обоснование возможности получения дуговой траектории для цилиндрической заготовки на валках в форме однополостного гиперболоида. Применение такой технологически простой формы валков обеспечивает их универсальность, что особенно актуально в условиях машиностроительных предприятий при отсутствии специального дорогостоящего оборудования.