Металлический ведущий круг для обработки конических поверхностей представляет собой вал с нелинейчатой винтовой поверхностью, включающей рабочий участок, обеспечивающий базирование заготовок при обработке, и вспомогательный, создающий продольную подачу. Рабочий участок ведущего круга рассчитывают на основе кинематического условия огибания поверхностей, а вспомогательный участок — как след, оставленный круговинтовыми линиями окружностей сопряжения конической и торцевых поверхностей заготовки.
Шлифование винтовой поверхности с фасонным профилем осевого сечения требует специального профилирования круга. Данная задача рассмотрена, например, в работе [18]. Однако при высокой точности к профилю винтовой поверхности частая правка фасонного круга вызывает очевидные технологические трудности.
Поэтому целесообразно использовать упрощенную форму шлифовального круга (коническую), а задачу формообразования винтовой поверхности ведущего круга решать на основе оптимизации параметров процесса.
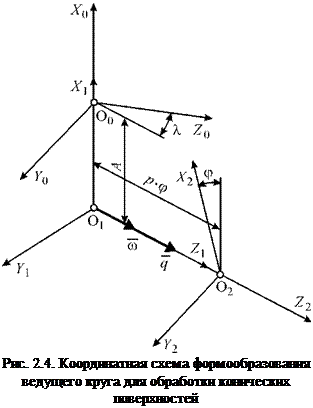 |
Введем в рассмотрение следующие координатные системы (рис. 2.4): S0(X0 O0 Y0 Z0) — система конического шлифовального круга; Si(X! 0i Yi Zi) — вспомогательная условно неподвижная система; S2(X2 02 Y2 Z2) — система ведущего круга. Система координат Si по отношению к системе S0 повернута вокруг оси X по часовой стрелке на угол X и смещена на величину А. Винтовое движение в системе S2 задано параметрамир и ф. На рис. 2.4 показана правая винтовая линия.
По аналогии с выводом формул в п. 1.2 получим выражения для семейства поверхностей ведущего круга с помощью матричных преобразований координат:
X2 = (X0 + A) cos ф + (Y cos X — Z0sin X) sin ф;
![]() Y2 = —(Xq + A) sin ф + (Y0 cos X — Z0sin X) cos ф; >
Y2 = —(Xq + A) sin ф + (Y0 cos X — Z0sin X) cos ф; >
Z2 = Y0 sin X + Z0 cos X — рф,
где р — шаг винтовой линии; ф — угловой параметр винтового движения; А — кратчайшее межосевое расстояние (наладочный параметр); X — угол разворота оси шлифовального круга относительно ведущего круга (наладочный параметр).
Составим кинематическое условие в системе координат S0, связанной со шлифовальным кругом. Выражения для проекций скорости относительного движения:
Vx = Z0 sin X — Y0 cos X;
Vy = (X0 + A) cos X + p sin X; >
V = -(X0 + A)sin X + p cos X.
Кинематическое условие огибания поверхностей окончательно примет вид:
(Rcos sctgs-u)sin X cos& + (A cos X + psin X )cos s sin& + (pcos X-Asin X )sin s = 0, (2.7) где u, 0 — криволинейные координаты конической поверхности шлифовального круга; R — максимальный радиус круга; s — угол профиля круга.
Приведем характеристическое уравнение (2.7) к виду квадратного уравнения относительно параметра 0:
гдеc = (pcosX-AsinX)sins, d = (Rcos sctgs-u)sinX.
Совместное решение уравнений (2.6) и (2.8) с секущими плоскостями определяет осевое или торцевое сечения ведущего круга. Осевое сечение поверхности ведущего круга получим, приняв Y2 = 0:
u sin s sin 0 cos X — (Rctgs — u cos s ) sin X
![]()
![]() tgф =——————- —-— ———————- ;
tgф =——————- —-— ———————- ;
u sin p cos 0 + A
_ u sin s cos 0 + A
X 2 = ’ cos ф
Z2 = u sin s sin 0 sin X + (Rctgs — u cos s) cos X — pф.
Кинематическое условие, составленное для торцевой круговой поверхности:
sin 0 = l+pcss. (2.10)
r
Анализ уравнения (2.10) показал, что при А + pctgs > ri значение угла 0 является иррациональным и вследствие этого контактная линия располагается вне круговой поверхности радиуса R. Поэтому так же, как и при профилировании, формировать вспомогательную часть винтовой поверхности ведущего круга будут окружности сопряжения конической и торцевых поверхностей.
Переходная кривая будет получена на ведущем круге, если сообщить окружности основания шлифовального круга в системе S0 винтовое движение (осевое сечение):
‘«T — . „ . . — —
Г sm 0 cos К — z sm К
![]() X2 = (r cos 0 + A)cos ф + (r sin 0 cos К — z sin К)sin ф; > Z2 = r sin 0 sin К + z cos К — рф.
X2 = (r cos 0 + A)cos ф + (r sin 0 cos К — z sin К)sin ф; > Z2 = r sin 0 sin К + z cos К — рф.
где ri, 0 — криволинейные координаты шлифовального круга; zi — координата, задающая положение шлифовального круга.
В табл. 2.5 приведен пример шлифования профиля валка по данным табл. 1.3. Исходные параметры: максимальный радиус круга RKp = 150,0 мм; шаг винтовой линии р = 25,0 мм. Наладочные параметры: межосевое расстояние А = 290,755 мм; угол перекрещивания осей К = 7,349°; угол профиля шлифовального круга в = 4°; ширина круга l1 = 20 мм. Полученные при шлифовании параметры профиля ведущего круга: ц1 = 3,988°; f1 = = -0,0027 мм.
Таблица 2.5
|
Профиль ведущего круга для обработки конических поверхностей, полученный при шлифовании
|
Таким образом, для формообразования нелинейчатой винтовой поверхности шлифовальным кругом с конической производящей поверхностью требуется решение задачи параметрической оптимизации в рамках уравнений (2.9), (2.11). При этом необходимо обеспечить заданный минимальный радиус ведущего круга и угол профиля ц1 = ц. Величина стрелы прогиба f1 может быть больше заданной, но того же знака (направлена в тело круга). Ширина переходных кривых должна укладываться в конструктивные размеры ведущего круга, полученные на этапе профилирования. В качестве оптимизируемых параметров выступают: межосевое расстояние А, угол перекрещивания К, угол профиля круга в. Также требуется коррекция ширины l1 шлифовального круга по сравнению с шириной l рабочего участка ведущего круга. Шаг винтовой линии р принимают равным шагу винтовой линии ведущего круга. Максимальный радиус шлифовального круга RKp выбирают по технологическим соображениям.
На основе численного анализа наладочных параметров при шлифовании ведущего круга можно сделать следующие выводы:
• увеличение углов X и 8 приводит к увеличению угла профиля Ці ведущего круга, величины стрелы прогиба fl и уменьшению ширины переходных кривых;
• снижение радиуса круга RKp вызывает уменьшение параметра fl, а на угол ці оказывает неоднозначное влияние;
• увеличение наладочного параметра А при прочих равных условиях способствует уменьшению параметра f и слабо влияет на угол ц1.
