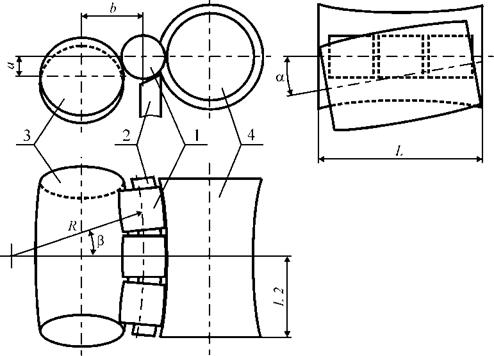
Детали цилиндрических и конических роликоподшипников для повышения долговечности выполняют с профилем, обеспечивающим локализацию площадок контакта. Если осевой профиль задан дугой окружности, то такие поверхности называют бомбинированными.
Бесцентровое шлифование бомбинированных поверхностей осуществляют двумя методами — с поперечной подачей (врезанием) и с продольной подачей (на проход). Метод бесцентрового шлифования с поперечной подачей отличается простотой наладки станка, но малопроизводителен и трудно автоматизируем. Поэтому в условиях массового производства предпочтение отдают шлифованию с продольной подачей.
При бесцентровом шлифовании на проход требуется рассчитать профиль ведущего круга и наладочные параметры станка. Однако до настоящего времени отсутствовали строгие математические модели для описания формообразования бомбинированных поверхностей. В результате не всегда достигалась требуемая точность обработки, что ограничивало применение данного высокопроизводительного процесса.
Рассмотрим геометрические аспекты бесцентрового шлифования бомбинированных поверхностей. Предлагаемый подход к аналитическому описанию процесса формообразования основан на том, что форма продольного сечения заготовки 1 однозначно определяется траекторией ее движения относительно шлифовального круга 4 (рис. 1.13). При образовании бомбинированной поверхности траектория движения исходно цилиндрической заготовки — дуга окружности радиуса R. Ось заготовки в любой момент является «огибаемой» к окружности радиуса R и имеет линейчатое касание с ведущим кругом 3. Продольная подача создается силами трения за счет поворота оси ведущего круга на угол а относительно плоскости, в которой расположена траектория движения заготовки. Для устойчивого формообразования ось заготовки обычно устанавливают выше оси ведущего круга на величину а. Опорный нож 2 имеет криволинейную форму.
|
Рис. 1.13. Схема бесцентрового шлифования бомбинированных поверхностей |
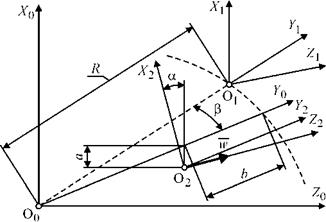
Для расчета поверхности ведущего круга введем в рассмотрение следующие координатные системы (рис. 1.14): £о№ O0 Y0 Z0) — условно неподвижная система; O1 Y1 Z1) — система заготовки; S2(X2 O2 Y2 Z2) — система ведущего круга. Система координат S1 по отношению к системе S0 повернута вокруг оси X на угол Р и смещена по оси Y на величину R. Система координат S2 по отношению к системе S0 повернута вокруг оси Y на
|
Поверхность цилиндрической заготовки в векторно-параметрической форме в системе S0 зададим уравнением:
r0 =-rsin S — i — rcos S — j +1 — k, (1.25)
где r — радиус заготовки; S, l — криволинейные координаты поверхности цилиндрической заготовки.
Уравнения в декартовой системе координат, описывающие семейство поверхностей ведущего круга, получим при переходе от системы S1 через So к системе S2 с помощью векторно-матричных преобразований:
X2 = — r sin S cos a — Q sin а + a;
![]() Y = — r cos S cos P +1 sin P + R(cos P -1) + b; > Z2 = — r sin S sin a + Q cos a,
Y = — r cos S cos P +1 sin P + R(cos P -1) + b; > Z2 = — r sin S sin a + Q cos a,
где Q = (rcosS-R)sinp + lcosp; a — угол поворота ведущего круга; P — независимый угловой параметр; R — радиус траектории движения заготовки; а — вертикальный наладочный параметр станка; b — горизонтальный наладочный параметр станка.
Для выявления контактной линии на семействе поверхностей ведущего круга, определенных уравнениями (1.26), так же, как и ранее, используем условие пересечения нормали к поверхности заготовки с осью ведущего круга, заданной единичным вектором w. Такой подход справедлив, если скорость вращения заготовки многократно превышает скорость ее продольной подачи.
Составим кинематическое условие, аналогично п. 1.1, в системе координат S1:
a — rsinS b — R( 1 — cos P) — rcos S l — RsinP
sin a — cos a sin P cos a cos P
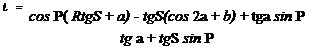 |
|
Решение уравнения (1.27) позволяет связать между собой криволинейные координаты l и S. Более простую математическую формулу получим, если из уравнения (1.27) выразим координату l:
Таким образом, искомая поверхность ведущего круга описана уравнениями (1.26) и (1.28). Профиль ведущего круга задают координатами (Z2,
R2), где R =Jx[+y[. В этом случае число неизвестных параметров S, l, P превышает число составленных уравнений, поэтому требуется численный метод решения.
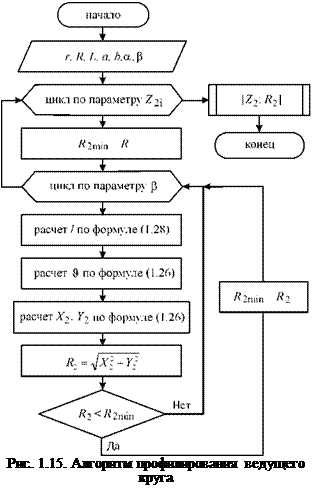 |
Алгоритм численного профилирования ведущего круга приведен на рис. 1.15 и сводится к следующему.
Организуют внешний цикл по переменной Z2i. В фиксированной торцевой плоскости Z2i = const находят следы ее пересечения заготовкой при различных углах P. Во внутреннем цикле по углу P независимым параметром выступает угол S, который определяют из третьего уравнения системы (1.26) при подстановке в него выражения (1.28). Затем по итерационной процедуре находят минимальный радиус ведущего круга R2min,
используя первое и второе уравнения системы (1.26). Анализ показал, что при точности определения радиуса круга 0,1 мкм целесообразно ограничиться точностью угла Р, равной 0,05°. Данная рекомендация позволит снизить затраты машинного времени при обеспечении заданной точности расчета.
Примеры расчета профиля ведущего круга шириной L = 400 мм для различных параметров наладки бесцентрового шлифовального станка приведены в табл. 1.7 — 1.10.
Таблица 1.7
Профиль ведущего круга для обработки бомбинированных поверхностей:
r = 10 мм, R = 1000 мм, a = 5 мм, b = 100 мм, а = 2°
|
Z2, мм |
X2, мм |
Y2, мм |
R2, мм |
l, мм |
V, градус |
3,градус |
|
-200 |
10,974 |
69,631 |
70,490 |
4,155 |
11,90 |
5,793 |
|
-150 |
9,297 |
78,607 |
79,155 |
1,421 |
8,80 |
5,394 |
|
-100 |
7,664 |
84,968 |
85,313 |
0,881 |
5,85 |
4,749 |
|
-50 |
6,063 |
88,760 |
88,966 |
0,082 |
2,90 |
3,916 |
|
0 |
4,488 |
90,013 |
90,125 |
0,018 |
0 |
2,933 |
|
50 |
2,927 |
88,740 |
88,788 |
-0,045 |
-2,90 |
1,873 |
|
100 |
1,366 |
84,931 |
84,942 |
0,020 |
-5,80 |
0,810 |
|
150 |
-0,206 |
78,557 |
78,558 |
-1,382 |
-8,80 |
-0,187 |
|
200 |
-1,800 |
69,574 |
69,597 |
-4,115 |
-11,90 |
-1,053 |
|
Таблица 1.8 Профиль ведущего круга для обработки бомбинированных поверхностей: r = 10 мм, R = 1000 мм, a = 15 мм, b = 100 мм, а = 3°
|
|
Таблица 1.9 Профиль ведущего круга для обработки бомбинированных поверхностей: r = 5 мм, R = 500 мм, a = 15 мм, b = 100 мм, а = 2°
|
|
Таблица 1.10 Профиль ведущего круга для обработки бомбинированных поверхностей: r = 10 мм, R = 2000 мм, a = 15 мм, b = 100 мм, а = 2°
|
Анализ табл. 1.7 — 1.10 показал, что профиль ведущего круга представляет собой несимметричную относительно плоскости Z2 = 0 выпуклую кривую. Радиус ведущего круга больше на той части профиля, которая располагается ниже центра О2 оси круга, при положительном значении параметра а (см. рис. 1.14).
С увеличением угла а профиль изменяется таким образом, что увеличивается его несимметричность относительно плоскости Z2 = 0. При радиусе траектории R, равном или меньшем ширине круга L, возникает так называемое подрезание профиля. Указанный эффект заключается в том, что профиль круга теоретически формируется при значениях l, превышающих действительные геометрические размеры заготовки. При этом радиус круга становится меньше, чем образованный заготовкой заданной длины.
Профиль ведущего круга может быть аппроксимирован дугой окружности, радиус и положение центра которой зависят как от размеров заготовки, так и от наладочных параметров станка. Результаты расчета параметров аппроксимирующей окружности, выполненные по методу наименьших квадратов, приведены в табл. 1.11, где R1 — радиус аппроксимирующей окружности; s — координата положения центра окружности по оси Z2; F — значение целевой функции.
Таблица 1.11
|
Параметры аппроксимирующей дуги окружности для профиля ведущего круга при обработке бомбинированных поверхностей
|
Анализ табл. 1.11 показал, что радиус аппроксимирующей дуги окружности R1 несколько больше радиуса траектории движения R и возрастает с увеличением радиуса r заготовки. Вертикальный наладочный параметр а обычно назначают, исходя из стабильности силового взаимодействия при бесцентровом шлифовании. Однако параметр а также оказывает влияние на профиль ведущего круга — его увеличение способствует формированию более рационального профиля круга с меньшими отклонениями углов контакта по длине обработки.