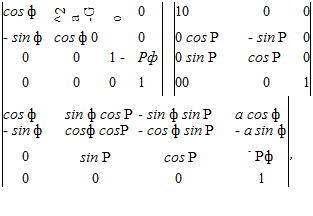При изготовлении сложных поверхностей (в том числе конических) бесцентровое шлифование с продольной подачей имеет ряд ограничений. Это обусловлено необходимостью создания сложной траектории движения заготовки, которая при этом должна иметь постоянный контакт с базирующими элементами станка — ведущим кругом и опорным ножом. До настоящего времени описание геометро-кинематических аспектов бесцентрового шлифования конических поверхностей не нашло отражения в технической литературе.
Обработку конических поверхностей ведут на специальных станках (например, модель ВШ-818 завода «Вистан», Беларусь) или на модернизированных бесцентровых круглошлифовальных станках с широким кругом (например, модель SASL 5/2 фирмы Mikrosa, Германия). В последнем случае станок оснащают ведущим кругом (барабаном) с винтовой канавкой сложного профиля.
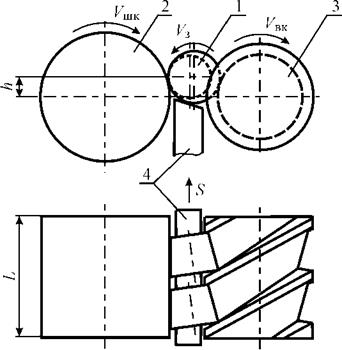
Рассмотрим процесс формообразования конических поверхностей при бесцентровом шлифовании и методику расчета профиля ведущего круга. При шлифовании заготовка 1 базируется и перемещается таким образом, что образующая ее конической поверхности параллельна оси цилиндрического шлифовального круга 2 станка (рис. 1.8). Обеспечить непрерывное движение такого вида можно только винтовым движением заготовки относительно шлифовального круга. Основным элементом, создающим круговую и продольную подачи, будет ведущий круг 3. Если ось ведущего круга перекрещивается с осью заготовки, то винтовая поверхность, образованная конической поверхностью заготовки при их относительном движении, является нелинейчатой. При этом часть винтовой поверхности ведущего круга, контактирующую с образующей конуса заготовки и базирующую ее, назовем рабочей, а другую часть, контактирующую с основанием усеченного конуса и обеспечивающей продольное перемещение — вспомогательной. Нож 4 выполняет функцию дополнительной опоры, от его положения зависит стабильность вращения заготовки, однако траекторию движения он не формирует. Для принятой схемы формообразования с использованием цилиндрического шлифовального круга опорный нож имеет сложную криволинейную поверхность. Также в качестве опорного элемента вместо ножа применяют вращающийся ролик фасонного профиля.
|
Рис. 1.8. Схема бесцентрового шлифования конических поверхностей |
Введем в рассмотрение следующие координатные системы (рис. 1.9): S0(X0 O0 Y0 Z0) — система заготовки; S1(X1 O1 Y1 Z1) — вспомогательная
 |
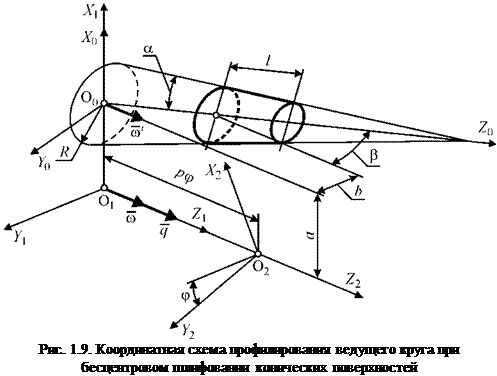условно неподвижная система; S2(X2 O2 Y2 Z2) — система ведущего круга. Система координат Si по отношению к системе S0 повернута вокруг оси X против часовой стрелки на угол Р и смещена по оси X на величину а. Винтовое движение в системе S2 задают параметры р и ф. Дальнейшие расчеты приведены для правой винтовой линии (вектора ш и q имеют одинаковое направление). Заготовка представлена в виде усеченного конуса длиной l, расположенного на расстоянии b по оси Y в системе S0.
Задача профилирования ведущего круга состоит в нахождении винтовых поверхностей, формируемых образующей и основаниями конической заготовки.
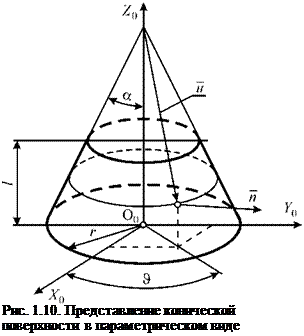
Коническую поверхность заготовки в системе S0 опишем в параметрическом виде (рис. 1.10):
X0 = usin a cos X Y0 = usin a sin X Z0 = Rctga — u cos a,
где u, & — линейная и угловая криволинейные координаты; a — угол образующей конуса заготовки; R = r + btgaIsinfi — радиус основания продолженного конуса; r — радиус основания конуса заготовки (максимальный радиус заготовки); Р — угол перекрещивания осей заготовки и ведущего круга; b — наладочный параметр.
Поверхность основания заготовки опишем как поверхность круга следующими уравнениями:
X0 = r cos S; Y = rtsin S; > Z 0 = z,-
 |
где ri, S — криволинейные координаты круга; zi — координата, задающая осевое положение круга (ri = R — zi tgo).
Поверхность ведущего круга найдем как геометрическое место контактных линий в системе S2. Уравнения поверхности ведущего круга в векторной форме:
r = Ф rn;
n — V = о,
где M20 — матрица перехода от системы S0 к системе S2; n — вектор нормали к поверхности; V — вектор скорости относительного движения.
Матрица перехода M20 имеет вид:
где а — кратчайшее межосевое расстояние заготовки и ведущего круга; р — шаг винтовой канавки; ф — угловой параметр винтового движения.
Используя формулы (1.12) и (1.13), осуществим переход от системы S0 к системе S2:
X2 = Xlcos ф + Ylsin ф cos Р-Zlsin ф sin Р + acos ф; Y2 = — X1 sin ф + Y cos ф cos Р — Z cos ф sin Р — a sin ф; > Z = Ysin Р + Zcos Р-рф.
Кинематическое условие огибания поверхностей в общем виде:
n — V = nXx + nyvy + nXz = 0. (1.15)
Относительное движение заготовки и ведущего круга определено скользящим вектором угловой скорости о и свободным вектором поступательного движения q = р о (см. рис. 1.9). Приведем вектор о к точке О0, заменив его вектором о’ = о и вектором-моментом m (о) = R х о.
Тогда выражение для скорости относительного движения:
V = о’х r + R х о + ро,
где r — радиус-вектор текущей точки поверхности заготовки; R — радиусвектор точки приложения скользящего вектора о.
Вектор о в системе координат детали определен координатами:
юх = о’х = 0; оу = о’y = sinP; ог = о’z = cosp. Проекции скорости определим по известным формулам:
Vx = о’уК — о’zry + К0z — Коу + Рхох;
Vy = о’ Кх — о’xrz + Г’ох — Коz + Руоу;
Vz = о’хКу — о’ уГх + Коу — ГУох + Р20z.
В окончательном виде выражения для проекций скорости относительного движения:
V = (Rctga — u cos a) sin Р — u sin a cos Р sin Я;
V 
= usin a cos Р cos Я + acos Р + psin Р;
V = — usin a sin Р cos Я-asin Р + pcos Р.
Проекции единичного вектора нормали к поверхности заготовки:
nx = cos a cos Я; n^ = cos a sin Я; >
n = sm a.
Не нарушая общности, положим о = 1 рад/с. Тогда после преобразований выражение (1.15) примет вид:
(Rctg a cos a — u)sin Р cos Я + (acos Р + psin Р )cos a sin Я + (pcos Р — asin Р )sin a = 0. (1.18) Уравнение (1.18) относительно переменной Я является трансцендентным, однако его можно преобразовать в квадратное уравнение, введя замену переменной, как сделано в работе [28]:
? З З
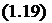(A — B)tg — + 2 cos a(acos P + psin P )tg — + A + B = 0,
где A = (pcos P — asinP)sina; B = (Rctgacos a — u)sinP.
Уравнение (1.19) устанавливает связь между криволинейными координатами и и З. Данное квадратное уравнение имеет два решения, соответствующих двум контактным линиям. При внешнем огибании поверхностей следует выбирать корень с положительным знаком перед радикалом.
Уравнения (1.11) и (1.14) описывают семейство поверхностей ведущего круга. Уравнение (1.19) позволяет выделить контактные линии на этом семействе поверхностей, то есть их совместное решение определяет одну искомую поверхность ведущего круга.
Таким образом, поверхность ведущего круга бесцентрового шлифовального станка описана выражениями (1.11), (1.14) и (1.19). Совместное решение этих уравнений с секущими плоскостями дает осевое, торцевое или нормальное сечения. На практике удобнее использовать осевое сечение винтовой поверхности, которое получим, приняв Y2 = 0:
Х2 = (usin a cos З + a)cos ф + C sin ф;
 |
 |
 |
 |
Z2 = usin a sin З sin P + (Rctga — ucos a )cos P — b /tgP — рф;
где C = u(sin З sin a cos P — cos a sin P) — Rctga sin P.
Система уравнений (1.20) описывает в параметрической форме осевое сечение ведущего круга. Хотя в формулы входят три переменные u, З и ф, но независимых параметров только два. Поэтому уравнения решают относительно переменных З и ф при фиксированных значениях параметра u. Диапазон изменения параметра u, соответствующий длине заготовки l, выявляют из последнего уравнения системы (1.11).
Вспомогательная часть поверхности ведущего круга образуется основаниями конуса заготовки. Кинематическое условие для поверхности основания заготовки имеет вид:
coSз = — acgp+P. (1.21)
z,
Анализ уравнения (1.21) показал, что при actgP + p > zt значение искомого угла З иррационально, то есть геометрическое решение задачи отсутствует. Описанная ситуация характерна для реальных наладочных параметров бесцентрового шлифовального станка, поэтому контактная линия располагается вне радиусов оснований. Тогда вспомогательную часть вин
товой поверхности ведущего круга сформируют окружности сопряжения конической поверхности и плоскостей основания заготовки, у которых вектор нормали не определен. В теории зубчатых зацеплений такие поверхности получили название переходных [24].
Переходные поверхности будут получены на ведущем круге, если сообщить окружности основания конуса в системе S0 винтовое движение. Уравнения осевого сечения переходных поверхностей:
Г sin $ cos P — z sin P,
Г cos $ — a
r(cos $ cos ф + sin $ cos P sin ф) — z sin P sin ф + a cos ф; > Г sin $ sin P + z cos P — рф — b / tgP.
Таким образом, поверхность ведущего круга для обработки конических деталей представляет собой нелинейчатую винтовую поверхность, состоящую из рабочего участка, базирующего заготовки при обработке, и вспомогательного, обеспечивающего продольную подачу. Рабочий участок ведущего круга определяют по формулам (1.20) на основе кинематического условия огибания поверхностей, а вспомогательный участок — по формулам (1.22) как след, оставленный круговинтовыми линиями окружностей сопряжения конической поверхности и плоскостей основания заготовки.
Рассмотрение рабочего и вспомогательного участков ведущего круга в общей системе координат позволяет оценить характер их сопряжения и построить винтовую поверхность в целом. Численный анализ показал, что для реальных наладок станка рабочий и вспомогательный участки профиля имеют плавное сопряжение с одной точкой контакта.
При выборе наладочных параметров станка следует иметь в виду, что угол P в отличие от параметров а и b не устанавливается непосредственно, а является расчетным (как правило, полагают P = а). Кратчайшее межосевое расстояние а назначают, исходя из условий стабильного силового взаимодействия при шлифовании. Параметр а может принимать как положительные, так и отрицательные значения. Так, при металлическом ведущем круге с коэффициентом трения менее 0,2 целесообразно располагать заготовку ниже линии, соединяющей оси шлифовального и ведущего кругов.
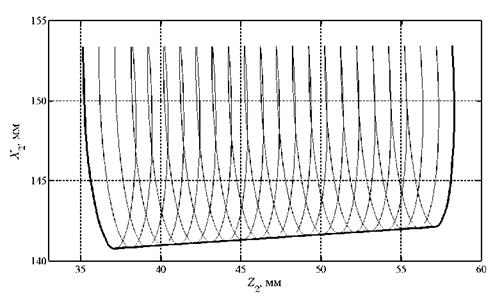
Примеры расчета осевого профиля ведущего круга для обработки конических заготовок с различными размерами при различных комбинациях параметров наладки станка даны в табл. 1.3 — 1.5. Изображение профиля ведущего круга для примера из табл. 1.3. приведено на рис. 1.11.
|
Таблица 1.3 Профиль ведущего круга для обработки конических поверхностей: r = 10 мм, а = 2°, l = 20 мм, а = 15 мм, b = 150 мм, Р = 2°, p = 25 мм
|
|
Таблица 1.4 Профиль ведущего круга для обработки конических поверхностей: r = 20 мм, а = 5°, l = 20 мм, а = 20 мм, b = 170 мм, Р = 5°, p = 25 мм
|
|
Рис. 1.11. Профиль ведущего круга для обработки конических поверхностей: r = 10 мм, а = 2°, l = 20 мм, а = 15 мм, b = 150 мм, Р = 2°, p = 25 мм |
|
Таблица 1.5 Профиль ведущего круга для обработки конических поверхностей: r = 30 мм, а = 2°, l = 20 мм, а = -20 мм, b = 200 мм, Р = 2°, p = 25 мм
|
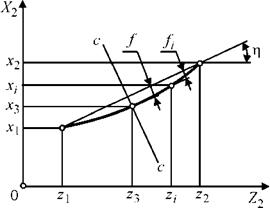
В общем случае рабочий участок осевого сечения ведущего круга криволинейный. Для оценки такого профиля целесообразно использовать параметры: угол профиля ц и максимальную стрелу прогибаf (рис. 1.12).
|
Рис. 1.12. Схема для определения параметров рабочего участка профиля |
Угол ц рабочего участка профиля ведущего круга определяют по формуле:
ц = arctg———, (1-23)
22 —
где х1, х2, z1, z2 — координаты крайних точек осевого сечения профиля.
Стрелу прогиба профиля в произвольной точке с координатами (xi, z) находят по формуле:
f = Akl — Ы — (z1 — z,)tgnJ cos ц •
Для реальных наладок станка профиль близок к симметричному относительно прямой с-с (см. рис. 1.12). В этом случае максимальную стрелу прогиба определяют в средней точке с координатами (х3, z3):
f = (|хх| — |x3[)cos ц + — z3)sin ц , (1-24)
где х3, z3 — координаты средней точки осевого сечения профиля.
При положительном значении величины f — профиль ведущего круга выпуклый, а при отрицательном значении — вогнутый.
Практическое значение для изготовления ведущего круга имеет ширина переходных кривых h1 и h2 (h1 — ширина переходной кривой, образованной большим основанием усеченного конуса, h2 — ширина переходной кривой, образованной меньшим основанием), которая определяет дополнительные участки профиля и шаг винтовой поверхности. Параметры hi и h2 находят как разность координат Z2, соответствующих крайней точке переходной кривой и точке ее сопряжения с основным участком профиля.
Для примеров, приведенных в табл. 1.3 — 1.5 рассчитаны параметры профиля, которые даны в табл. 1.6.
Таблица 1.6
Параметры профиля ведущего круга для обработки конических поверхностей
|
Исходные данные |
Расчетные параметры профиля |
|||
|
Ц, градус |
f мкм |
hi, мм |
h2, мм |
|
|
Табл. 1.3 |
3,988 |
-0,005 |
2,15 |
1,21 |
|
Табл. 1.4 |
9,954 |
-0,03 |
4,31 |
1,41 |
|
Табл. 1.5 |
3,992 |
-0,002 |
4,84 |
2,95 |
Анализ табл. 1.6 показал, что типичный осевой профиль ведущего круга имеет криволинейную вогнутую форму со стрелой прогиба в пределах 0,001 мм. Профиль зависит как от размеров обрабатываемых деталей, так и от выбора значений наладочных параметров бесцентрового шлифовального станка. Угол профиля ц валка всегда больше, чем угол а конической детали и обычно удовлетворяет соотношению ц = (1,5.. ,2)-а.