Впервые задачи профилирования и правки ведущего круга бесцентровых шлифовальных станков были исследованы, а затем развиты в работах [14, 21]. Однако в указанных работах полученные решения имели приближенный характер и ряд неточностей. Так, весьма критично утверждение, приведенное в работе [14], что «теоретически точный» профиль ведущего круга может быть получен в результате «обкатывания» заготовки определенного радиуса по гиперболе. В последующих работах [17, 21] данный факт не подвергался сомнению. Строгая математическая модель для расчета профиля ведущего круга приведена в работах [17, 26]. В ней рассмотрена новая схема с поворотом оси круга в вертикальной и горизонтальной плоскостях, а непрерывный столб заготовок представлен как конус с учетом постепенного съема припуска. Однако такое представление последовательности заготовок при шлифовании имеет как преимущества, так и недостатки по сравнению с традиционным. Очевиден тот факт, что при указанной схеме обработки цилиндрическая поверхность будет окончательно формироваться только на торце ведущего (и шлифовального) круга. Кроме того, в настоящее время рассмотренный способ не получил широкого применения в производстве.
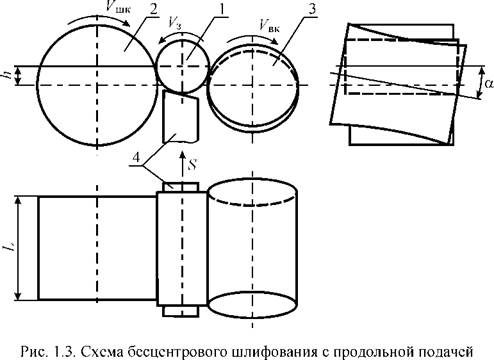
Требуемая точность обработки на бесцентровых шлифовальных станках с продольной подачей в значительной степени определяется траекторией движения заготовки 1, которая, в свою очередь, зависит от геомет-
рии и взаимного положения основных элементов формообразующей системы — шлифовального 2 и ведущего 3 кругов, опорного ножа 4 (рис. 1.3). Оси шлифовального круга и заготовки параллельны друг другу. Вращательное V3 и прямолинейно-поступательное S движения подачи заготовке сообщает ведущий круг. Для создания продольной составляющей подачи за счет сил трения ось ведущего круга перекрещивается с осью заготовки под углом а. Для обеспечения устойчивого формообразования ось заготовки обычно устанавливают выше осей кругов на величину h [14, 17, 21]. На бесцентровых шлифовальных станках с широкими кругами (шириной L) одновременно обрабатывают несколько заготовок, последовательность которых можно представить как виртуальный цилиндр того же радиуса.
|
|
Ведущий круг должен иметь непрерывное линейное касание с заготовкой (виртуальным цилиндром) при перекрещивании их осей. Выполнение данного условия при стабильности кинематических параметров процесса обеспечивает достижение высокой точности обработки.
Определим поверхность ведущего круга как огибающую к поверхности заготовки при ее относительном движении с учетом принятых параметров наладки станка. Для этого введем следующие координатные системы (рис. 1.4): S1 (X1 O1 Y1 Z1) — система координат заготовки, S2 (X2 O2 Y2 Z2) — система координат ведущего круга. Система координат S2 по отношению к системе S1 повернута относительно оси Y по часовой стрелке на угол а и смещена по оси X на величину — h и по оси Y на величину — e.
Поверхность ведущего круга найдем как совокупность линий контакта круга и заготовки. Для расчета искомой поверхности необходимо 10
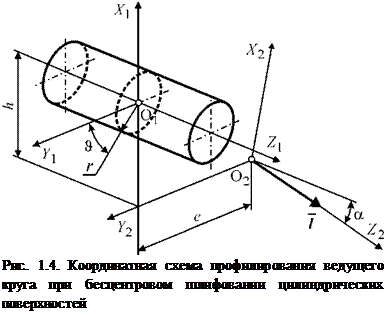 |
совместить координатную систему S1 с системой S2 с помощью векторноматричных преобразований и выделить контактные линии по кинематическому условию.
Поверхность цилиндрической заготовки (виртуального цилиндра) в векторно-параметрической форме в системе Si опишем уравнением:
Г = — rsin i + rcos & • j + z • k, (1-1)
где r — радиус заготовки; S, z — криволинейные координаты цилиндрической поверхности.
Для преобразования координат поверхности заготовки из системы S1 в систему S2 воспользуемся матричным равенством:
r2 = M21 • Г1 ,
где М21 — матрица перехода из системы координат S1 в систему S2.
Матрица перехода М21 имеет вид:
cos а 0 sin а h
0 10 е
M21 = • n п ,
— sin а 0 cos а 0
0 0 0 1
где а — угол перекрещивания осей ведущего круга и заготовки; е — кратчайшее расстояние между осями заготовки и ведущего круга; h — вертикальное смещение заготовки относительно круга.
В проекциях уравнения, описывающие семейство поверхностей ведущего круга:
X = — rsin S cos а + zsin а + h;
![]() Y2 = r cos S + e;
Y2 = r cos S + e;
X = r sin S sin а + z cos а.
Для определения искомой поверхности валка по уравнениям (1.2) необходимо найти контактную линию или характеристику из основной теоремы пространственных зацеплений [24]. В точке касания взаимно огибаемых поверхностей вектор скорости относительного движения должен лежать в плоскости, касательной к данным поверхностям. Аналитический эквивалент приведенной теоремы — условие ортогональности векторов нормали и скорости относительного движения, выраженное равенством нулю их скалярного произведения:
n — V = 0, (1.3)
где n — нормаль к поверхностям в контактной точке; V — скорость относительного движения.
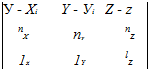 |
||
При наличии в передачах так называемых осей зацепления возможно упрощение кинематического метода. Тогда характеристическое уравнение (1.3) принимает вид:
где Х, Y, Z — координаты поверхности заготовки; x, y, zt — координаты начала направляющего вектора 1 оси валка; nx, nY, nZ — компоненты единичного вектора нормали к поверхности заготовки; 1Х, 1Y, 1Z — компоненты направляющего вектора 1 оси валка.
Все координаты, входящие в определитель (1.4), задают в единой системе координат. Компоненты нормали к поверхности заготовки находят как векторные произведения частных производных выражения (1.1) по криволинейным координатам z и 0.
Определитель вида (1.4), составленный в системе координат S1:
|
h — rsin 0 |
rcos 0 + e |
z |
||
|
— sin 0 |
cos 0 |
0 |
= 0. |
(1.5) |
|
— sin a |
0 |
cos a |
Из выражения (1.5) установим связь между криволинейными координатами 0 и z:
,ф = . (1.6)
— e
Уравнение (1.6) относительно угла 0 имеет два решения 01 и 02 в интервале [0; 2л]. Геометрический смысл двух корней заключается в том, что на поверхности цилиндра в заданном сечении есть две контактные точки, нормали в которых пересекают ось ведущего круга, при этом 02 = = 01 + 180°. Поэтому при выборе корня следует учитывать октант, в котором располагается угол 01 в соответствии с принятым началом отсчета [27].
Окончательно уравнения поверхности ведущего круга:
X2 =-rsin $ cos a + zsin a + h; Y2 = rcos $ + e;
![]() Z2 = r sin $ sin a + zcos a; <
Z2 = r sin $ sin a + zcos a; <
lg$ = zc<ga+h.
— e
Профиль ведущего круга как тела вращения целесообразно задавать в цилиндрической системе координат (Z2, R2), где R =JX[+Y*. Координата Z2 є [-L/2; L/2] выступает в качестве фиксированного параметра. Тогда для определения криволинейной координаты $ необходимо решить следующее трансцендентное уравнение:
rsin a sin $ + (h — elg$)cos aclga-Z2 = 0. (1.8)
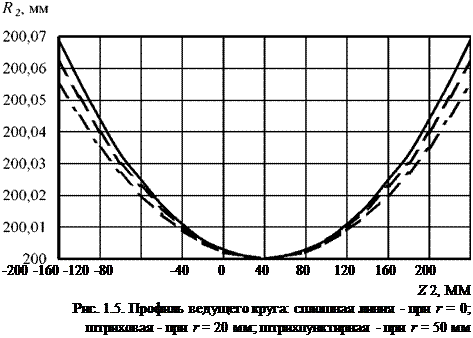 |
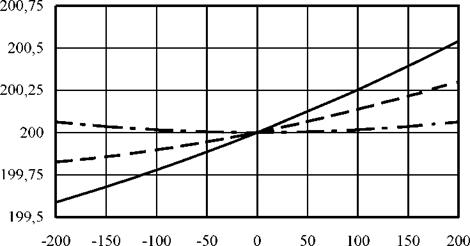
Рассчитанная по формулам (1.7) поверхность ведущего круга близка по форме к поверхности однополостного гиперболоида. Так, при радиусе заготовки, равном нулю, цилиндр превращается в прямую и образует од — нополостный гиперболоид. Поэтому полученную поверхность ведущего круга можно назвать квазигиперболоидной. На рис. 1.5 показан профиль ведущего круга, рассчитанный для трех значений радиуса заготовки r = 0; 20; 50 мм при параметрах наладки станка: a = 1,5°; h = 0; L = 400 мм; RШК = = 200 мм, где RШК — радиус ведущего круга в точке перекрещивания. Кратчайшее межосевое расстояние e рассчитано, исходя из приведенных данных.
Анализ рис. 1.5 показал, что кривизна профиля круга уменьшается с увеличением радиуса r заготовки. Существенное значение данный факт приобретает для бесцентровых шлифовальных станков с широкими кругами (L > 300 мм).
Исследуем влияние параметра h на профиль ведущего круга. Для этого рассчитаем профиль при различных значениях h. На рис. 1.6 представлен профиль ведущего круга, рассчитанный для следующих исходных данных: r = 20 мм; а = 1,5°; ЯШК = 200 мм; L = 400 мм; h = 0; 10; 20 мм.
|
R 2, мм
Z 2, мм Рис. 1.6. Влияние параметра h на профиль ведущего круга: сплошная линия — h = 20; штриховая — h = 10 мм; штрихпунктирная — h = 0 |
Из рис. 1.6 видно, что при h = 0 профиль ведущего круга симметричен относительно плоскости Z2 = 0. С ростом параметра h поверхность ведущего круга представляет собой часть поверхности квазигиперболоида, расположенную на соответствующем расстоянии от точки перекрещивания
О2. При этом увеличивается разность максимального и минимального радиусов профиля круга. К идентичным результатам приводит уменьшение кратчайшего межосевого расстояния е при прочих равных условиях.
Рассмотрим в качестве примера обработку заготовок диаметром 10 мм на станке модели МЕ397 при следующих параметрах: диаметр ведущего круга — 400 мм, диаметр шлифовального круга — 600 мм, ширина обоих кругов — 500 мм.
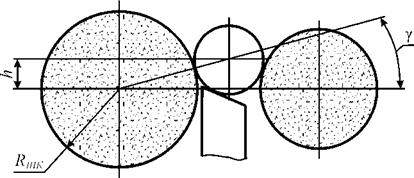
Для назначения высоты h имеются различные рекомендации. Например, в работе [21] величину h рассчитывают с учетом пяти параметров (диаметры заготовки, ведущего и шлифовального кругов, углы установки кругов относительно оси заготовки). Воспользуемся рекомендациями из работы [17], согласно которой h рассчитывают по формуле
h = (кшк + r)sin4, (1-9)
где у — угол между линией центров заготовки и шлифовального круга и линией центров кругов (рис. 1.7).
|
Рис. 1.7. Схема установки заготовки относительно шлифовального и ведущего кругов |
Угол у назначают в зависимости от вида обработки: 1° при черновой обработке, 3.. .3,5° — при получистовой, 4,5… 5° — при чистовой. Приняв у = 1° для черновой и у = 5° для чистовой обработки, получаем, согласно формуле (1.9), соответственно h = 5 мм и h = 26 мм.
Результаты расчета профиля ведущего круга для указанных исходных данных приведены в табл. 1.1 и 1.2. Угол перекрещивания осей ведущего круга и заготовки принят 1 ° для черновой обработки и 4° для чистовой обработки.
Таблица 1.1
|
Профиль ведущего круга для обработки цилиндрических поверхностей при черновой обработке: r = 5 мм, h = 5 мм, e = 200 мм, а = 1°
|
|
Таблица 1.2 Профиль ведущего круга для обработки цилиндрических поверхностей при чистовой обработке: r = 5 мм, h = 26 мм, e = 200 мм, а = 4°
|
Анализ табл. 1.1, 1.2 показал, что при рекомендуемых наладочных параметрах бесцентрового шлифовального станка профиль ведущего круга представляет собой плавную, монотонно возрастающую кривую. Угол контакта 0 круга с заготовкой уменьшается от входа к выходу из зоны обработки (согласно обозначению на рис. 1.4).