Система сил, развивающихся при микрорезании

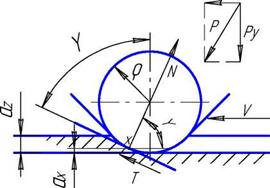
Рассмотрим случай микрорезания при поступательном перемещении ца­рапающего элемента, имеющего округлённую вершину радиусом р, на кото­рую действует сила P (рисунок 6.2).

Разложим эту силу на две составляющие Pz, Py(сила Pz срезает стружку, а сила Py прижимает зерно к обрабатываемой поверхности). В результате дей­ствия этих сил на передней поверхности зерна будут действовать реактивные силы, результирующие которых нормальная N и касательная T (сила трения), приложенная в точке X.

Pz Рисунок 6.2 — Система сил при микрорезании

Из условия равновесия сил имеем:

Pz = N • sin(90° — у) — T • sin у = N • (cos у — р • sin у)

Py = N • cos(90° — у) + T • cos у = N • (sin у + р — cos у) (*)

р — коэффициент трения.

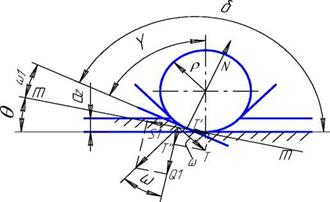
Определим силу N из условия прочности обрабатываемого материала на срез, для чего силу N и T разложим на составляющие, направленные по плоско­сти скалывания m-m и нормально к ней (рисунок 6.3) силы S и T’, и силы Qj и T " соответственно.

Рисунок 6.3 — Схема для расчёта сил S и Q

Результирующая S сил S1 и T’ является силой срезающей, преодолеваю­щей сопротивление металла скалыванию. Q — сжимающая металл сила в направлении, нормальном к плоскости скалывания. При этом:

S = Sj — T’ или S = N • sina + T • cos а

Q = Qj + T” или Q = N • cos а + T • sin а, т. к. а = 90° • (у + 0) и T = и N, то S = N • [cos(у + 0) — и • sin(у + 0)]

Q = N • [sin(у + 0) + и • cos(у + 0)] (**)

Допустив, что при деформировании поликристаллических тел в плоско­сти скалывания возникают силы трения, пропорциональные нормальному дав­лению, можно записать условие срезания слоя металла:

f’-тСр = S — и•Q,

где: f’- площадь срезаемого слоя; тСр — напряжения при срезе;

ju’ — коэффициент внутреннего трения деформируемого слоя металла в направлении плоскости скалывания.

f

Тогда, учитывая, что f’ =——- , где f — поперечная площадь царапания,

f •*

sin0

Подставив в это уравнение значения S и Q, по уравнениям (**) получим после преобразований:

f • Tcp

in 0[(1 — u • U) • cos(у + 0) — (u + U ) • sin(у + 0)]

f •*cp ■ (cos у — U — sin у) — u • U’) • cos(у + 0) — (и + U ) • sin f • Tcp ■ (sin у + и • cos у) — и • U) • cos( у + 0) — (и + U )• sin Py sin у + и • cos у Pz cos у — и • sin у

С учётом этого выражения, уравнения для сил Py и Pz запишутся:

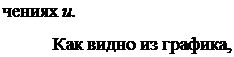На рисунке 6.4 приведён график зависимости — P — от упри различных зна­

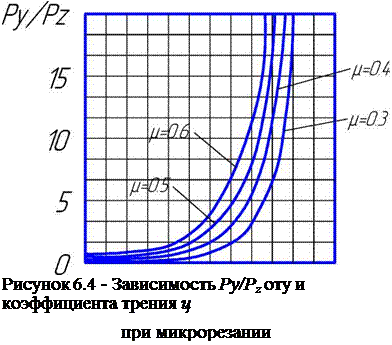него угла (-у), а при (-у) ~ 60° отношение р ^ ю.

20 40 60 —

Определим условия, при которых начинается срезание стружки.

Скалывание элементов металла произойдёт в направлении, где величина силы N будет минимальной. В уравнении (А) числитель отличен от нуля, сле­довательно, минимум силы N будет получен при максимальном значении зна­менателя, т. е. необходимо исследовать на максимум знаменатель.

После взятия первой производной и необходимых преобразований полу­чим:

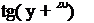sin( у + 20)

cos(у + 20) ц + ц

1 — tg*y= ctg( g+g) tgg ■ tgg

Запишем коэффициенты трения через углы трения

у + 20 = 90° — (g + g ).

Откуда 0 = 45° — у + ф + ф.

2

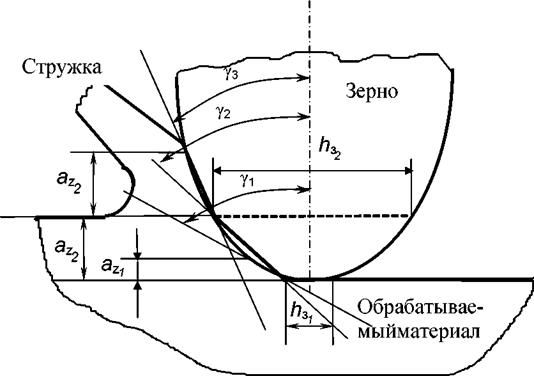
Анализ полученных уравнений позволяет сделать следующие выводы. Влияние толщины срезаемого слоя az на силы резания выражается через

фактический передний угол у (см. схему на рисунке 6.5).

При прочих равных условиях увеличение az приводит к уменьшению / у/, а следовательно, к снижению:

а) степени деформации металла;

б) условного напряжения резания и силы резания, необходимой для отде­ления стружки.

В зоне же особо тонких слоёв, для которых фактический угол резания (в том числе — у) является максимальным, происходит смятие слоёв движущимся зерном.

Рисунок 6.5 — Схема влияния глубины среза az, величины площадки износа h3 на зерне на передний угол у

Величина слоя ax, для которого происходит процесс отделения стружки,

определяется отношением —. Например, при царапании деталей из закалённой

Р

стали ШХ15 алмазным конусом с р = 6 мкм этот переход наблюдался при az = 6 мкм (рисунок 6.6).

О 1 2 3 6 5 6 2, мкм Рисунок 6.6 — Зависимость условного напряжения от толщины срезаемого слоя

С увеличением пластичности материала этот переход сдвигается в сторо­ну больших az. Таким образом, процесс микрорезания может происходить по

следующим возможным сценариям:

1) при малом давлении на материал (Py ^ 0) возможно только скольже­

ние зёрен по поверхности, тогда Pz = Py • ju-

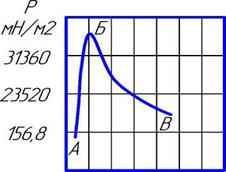
2) при возрастании Py до некоторой величины происходит упругое и пластическое деформирование материала зерном (участок АБ), тогда

Pz = —

где fi — сечение деформируемого слоя.

3)

при дальнейшем увеличении Py процесс сопровождается микрорезани-

зания:

U = Ul + U2 + U3 + U4 + U5 + U6,

где Ui — на деформирование обрабатываемого материала;

U2 — на диспергирование абразивного зерна;

U 3 — на трение;

U4 — на упругое деформирование;

U5 — на пластическое деформирование;

U6 — на остальное.

Влияние скорости V на силы резания неоднозначно. Повышение скоро­сти, с одной стороны, приводит к упрочнению металла за счёт увеличения ско­рости пластической деформации и снижению его пластичности.

С другой стороны, повышение скорости, а значит, и скорости деформа­ции влечёт за собой увеличение работы трения и, как следствие, температуры. В результате металл разупрочняется и снижается его сопротивление срезу. Ре­зультирующий эффект показан на графике (рисунок 6.7).

I — зона упрочнения, II — разупрочнения обрабатываемого материала Рисунок 6.7 — Зависимость силы резания Р от скорости