ОПТИМИЗАЦИЯ РЕЖИМОВ ШЛИФОВАНИЯ

Зависимости (5.4) — (5.6) показателей точности об­работки при наружном врезном шлифовании от режи­мов резания могут быть использованы для оптимиза­ции процесса.

В первом случае задача состоит ь том, чтобы най­ти такую совокупность значений режимов шлифования (независимых переменных Хг), при которой показатели точности обработки (зависимые параметры г/,) .прини­мают экстремальные значения. На себестоимость и производительность шлифования не накладывается ни­каких ограничений. При этом рассматривается следую­щая система исходных зависимостей:

Уъ— Ф2 (М> ■ і ^n)> Уч— с2>

Уз= ФзС^Ь -^21 • — • ; Яп), Уз~СЗі

………………………………………….. (5.7)

Ут—1 ~Фго—1 (Хь Мт — — • . Мі)? У т-1—Cm—I 1 Уі = фі(*Ь *2. — Хп)-э-1ШП

При т^п, где т — количество показателей качества деталей, ап — количество рассматриваемых техноло-

гических факторов, система (5.7) ае имеет решения. В случае, когда m<n> задача оптимизации сводится ) к нахождению экстремума функции (п—т) перемен­

ных:

Ух= • • • > (5.8)

полученной из исходной системы (5.7).

Задача оптимизации режима шлифования по кри­терию производительности состоит в отыскании сово­купности величин факторов хи при которой выбранный критерий стремится к экстремуму, а на показатели і точности обработки деталей, определяемые полученны­

ми зависимостями, заданы допустимые области их из — ; менения. В общем виде математическая модель опти-

[ мизации режима шлифования для этого случая пред­

ставляет собой систему уравнений и неравенств:

Уі= Ф; (х,, х2, хп), о,< Уі< bh / = (1. 2, 3 т),

(5.9)

i=(, 2, 3, п)

F ~ F (хі, ха, х„)-»-min (max).

Для решения этой модели в зависимости от формы аналитических выражений, входящих в нее, применя­ются методы линейного или нелинейного программиро­вания. Методы линейного программирования (сим­плекс-метод и его различные модификации) использу­ются в тех случаях, когда модель (5.9) состоит из линейных уравнений и неравенств, представляющих условия задач и целевую функцию. Когда целевая функция или ограничивающие условия выражаются в виде уравнений нелинейной формы, оптимальное ре­шение отыскивается с помощью методов нелинейного программирования.

При оптимизации по критерию производительности в качестве целевой функции может рассматриваться составляющая штучного времени обработки, обуслов­ленная режимами резания, которая для случая наруж­ного врезного шлифования может быть представлена в виде

Гд = —+*„■ (5-Ю)

s

После замены переменных £„= х и s = у в выражениях ‘ (5.4) — (5.6) и преобразований получается следующее обоб­щенное уравнение связи:

ОцХ2+2аXtxy 4- а22(/2+ с:,х -}- сс2у — f а0=0, (5.11)

где ац, а12, а22, а2, аь а0 — коэффициенты, полученные в результате преобразования исходных зависимостей.

Математическая модель (5.9) с учетом целевой функции (5.10) и обобщенного уравнения связи (5.1.1) для случая наружного врезного шлифования имеет вид

^МГН

як с2,

R г (з і

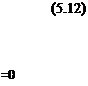t = С4,

■Г1< ^ — Г2, ^5і

Уі^У^Уіг Уъ<^с8,

ссц. у2+2к12хг/ + а22г/2 + аіхиагу2 + а0

7,= (/y + — t->min

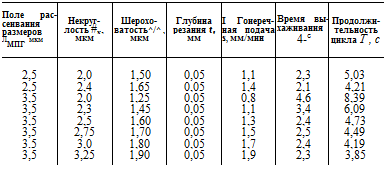
По модели (5.12) рассчитаны значения режимов реза­ния (поперечная подача, продолжительность выхажи­вания), позволяющие обеспечивать при заданной вели­чине припуска на обработку необходимые параметры

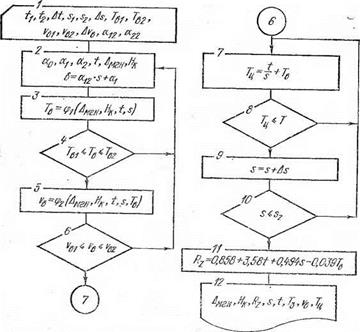
качества обрабатываемых деталей с максимальной про­изводительностью. Пример расчетных значений опти­мальных режимов бесцентрового врезного шлифования по критерию производительности обработки приведен в табл. 5.11. Алгоритм расчета представлен на рис. 5.24. В данном алгоритме при шаговой вариации величины

Рис. 5.24. Алгоритм расчета оптимальных режимов шлифования

поперечной подачи s в рассматриваемом диапазоне ее изменения и фиксированной t предусмотрено опреде­ление значений продолжительности выхаживания tB и длительности рабочего цикла обработки Тц. При этом выбираются значения режима, которые соответствуют минимальной величине Тц и удовлетворяют требовани­ям по качеству обрабатываемых деталей.

[1] / ІД**—

S = І/ ———————- , ‘ (1.5)