АНАЛИЗ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ

Колебательные процессы в металлорежущих станках часто рассматриваются как детерминированные. Это оправдывается, если исследовать колебания в течение короткого промежутка времени и не учитывать рабочих процессов (резание, трение, процессы в электродвига­теле и т. д.). Тогда при исследовании мы получим коле­бательный процесс с постоянной амплитудой и фазой, при этом применяется классический анализ Фурье.

В реальных же условиях при исследовании металло­режущих станков, записывая колебания, мы получаем одну из множества реализаций случайного процесса с различной амплитудой и фазой. Поэтому при исследо­вании колебаний металлорежущих станков целесооб­разно пользоваться методами теории случайных функ­ций. Различные характеристики случайного процесса колебаний несут информацию о протекании процесса. При решении практических задач обычно используются такие характеристики случайных процессов, как диспер­сия Dx(t), корреляционная функция Кх(х), спектраль­ная плотность Sx(u>), взаимная корреляционная функ­ция Кху(х), взаимная спектральная плотность Sxy((i>), функция когерентности v^ ■

Дисперсией случайного процесса называется такая функция аргумента t, значение которой при каждом t = U равно дисперсии Dx(ti) случайной величины x(U),

отвечающей значению аргумента при і=1%. Дисперсия характеризует разброс значений случайной величины около математического ожидания. Для непрерывной случайной величины она определяется выражением

Dx (t) = j [х (t) — Mx (*)]2 Ф (x) dx, (4.1)

где Mx (t) — математическое ожидание процесса х (/); Ф (х) — плотность распределения величины X.

При статистической обработке экспериментальных данных может быть определено среднее значение дис­персии по формуле

где x(ti) — среднее значение величины х при t = ti. Зна­чение Dx, определенное по формуле (4.2), не зависит от времени t в случае стационарного случайного процесса, описывающего колебания станочной системы в устано­вившемся режиме работы. Корреляционная функция показывает степень статистической зависимости между последовательными значениями случайного процесса. Аналитически для процесса x(t) она в общем виде опре­деляется выражением

Кх (т) = М[х (f) x(t-f т)], (4.3)

где т — временной сдвиг; М — символ математического ожидания.

Для дискретного случайного процесса

(4.4)

Так как колебания в станках в большинстве случаев являются следствием колебаний упругих элементов, то реализация случайного процесса будет включать в себя ансамбль синусоидальных кривых. Корреляционная функция синусоидального процесса определяется по вы­ражению
f!

2

(4.5)

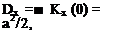(4.6)

где a — амплитуда; со — круговая частота.

Спектральная плотность Sx(со) показывает, как дис­персия процесса распределена по частотам:

1 00

5хИ=—— (X (т) dr. (4.7)

Здесь / = = V — 1. Для синусоидального процесса вида

х (I) • a cos (о„/ + b sin о>0/ (4.8)

спектральная плотность определяется выражением

Sx (w) = (со — со0) + 6 (со + соо)], (4.9)

где ©о — фиксированное значение частоты, т. е. спект­ральная плотность для полигармонического процесса представляет собой сумму 8-функций с коэффициентами, равными половине дисперсии.

Дисперсия процесса выражается через интеграл от спектральном плотности

оо

Dx= J Sx (о)) dco0. (4.10)

—oo

Часто необходимо сравнивать временные ряды, зна­чения которых измерены в разных масштабах, имеют различный физический смысл и различную спектраль­ную плотность. Разделив спектральную плотность на дисперсию процесса, получим нормированную спект­ральную плотность, которая отражает вклад дисперсии на определенных частотах в общую дисперсию.

Анализируя корреляционную функцию и спектраль­ную плотность, можно сделать определенные выводы о случайном процессе колебаний формообразующих узлов станка. Например, если корреляционная функция плав­но затухает при увеличении запаздывания, то спект­

ральная плотность принимает большие значения на низ­ких частотах и малые на высоких, что показывает доми­нирование низкочастотных колебаний в общем спектре. Увеличению частоты изменения значений корреляцион­ной функции соответствует рост значений спектральной плотности на высоких частотах.

Рассмотренные характеристики применяются для описания свойств и анализа процессов по их отдельным реализациям. Часто возникает необходимость исследо­вать общие свойства, присущие двум разным процессам, например установить амплитудную и частотную связи между колебаниями шлифовального круга станка и профилем обработанной поверхности детали. Для тако­го анализа могут быть использованы совместные харак­теристики двух случайных процессов, такие, как взаим­ные корреляционная функция и спектральная плотность, функция когерентности.

Взаимная корреляционная функция Кху(х) двух случайных процессов характеризует общую зависимость значений одного процесса от значений другого. Оценку величины взаимной корреляционной функции, связы­вающей значение процесса x(t) в момент времени t и значение процесса y(t) в момент t+т, можно найти, вычислив произведение

Кзд(т) = M[x(t)y{t + %) (4.11)

Используя КМ, можно, в частности, исследовать вре­мя и путь прохождения возмущающего воздействия. Для линейной системы, зная взаимную корреляционную функцию, связывающую сигналы на входе и выходе сис­темы, определяют время прохождения сигнала. Взаим­ная корреляционная функция будет иметь пик при сдвиге т, равном времени прохождения сигнала. Анало­гично можно определить и путь прохождения сигнала с учетом сдвига т, требуемого на его прохождение.

Для дискретных случайных процессов функция Кху(х) вычисляется по формуле

1 " — —

Кху (т) = lim—— У [х (*,) — х (f,) 1 [у (f,+т) — у (*,+т).

«-*oo гг

(4.12)

Взаимная спектральная плотность Sxy (со) позволяет про­вести анализ связи двух различных процессов х (I) и y(t) на различных частотах:

Для этих целей удобно использовать также функцию ко­герентности vz (со), которая определяется выражением

При равенстве 1 функция когерентности указывает на детерминированную связь между процессами на данной частоте, при равенстве 0 •— на независимость процессов друг от друга. Диализируя станочную систему с по­мощью функцин когерентности и взаимной спектраль­ном плотности, можно исследовать передаточные свой — пнн системі, і на фиксированных частотах и определить время прохождения сигнала как функцию частоты.