При шлифовании кругом, имеющим правильную форму, колебания линии контакта шлифовального круга и обрабатываемой детали можно представить в виде суммы гармонических функций:
|
П
|
Тогда профиль поверхности детали будет описываться огибающей семейства окружностей радиусом R-, центр которых движется по траектории, описываемой уравнениями (2.91), (2.92).
Уравнения огибающей имеют вид [25]:
где щ, bi — амплитуды соответственно вертикальных и горизонтальных колебаний; т — круговая частота; t — время; фі — угол сдвига фаз; v — скорость перемещения стола; R — радиус шлифовального круга.
Процесс формирования профиля поверхности детали как геометрическое копирование относительных колебаний шлифовального круга и обрабатываемой детали описан в работе [25]. При рассмотрении станка как замкнутой динамической системы возникает вопрос о силовом воздействии процесса шлифования на качество обрабатываемой детали.
Изменение условий обработки вследствие относительных колебаний должно влиять на силы резания через изменение параметров фактического сечения срезаемого слоя [16]. Для их вычисления рассматривается формирование профиля шлифованной поверхности исходя из кинематики процесса формообразования при плоском шлифовании периферией круга.
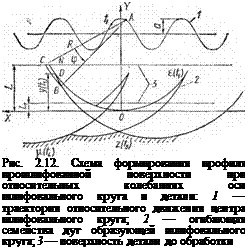
На рис. 2.12 представлена схема формирования поверхности при колебаниях центра шлифовального круга вдоль оси У и его движении относительно обрабатываемой детали вдоль оси X с постоянной скоростью V. При вычислении параметров сечения срезаемого слоя
будем предполагать, что колебания линии контакта содержат только одну гармоническую составляющую, т. е. уравнения движения центра круга имеют вид
(х = vt,
 |
= R — a —acosai.
Знак «минус» выбран потому, что профиль обрабатываемой детали образует нижняя огибающая. При определенных условиях, когда кривизна траектории относительно движения центра шлифовального круга больше кривизны шлифовального круга 1 /R, огибающая имеет петлю.
 |
Для определения профиля обработанной поверхности и параметров мгновенного сечения снимаемого слоя материала необходимо исследовать характерные точки огибающей и образующей шлифовального круга. Условие возникновения петли огибающей
 |
|
|
|
 |
 |
Если подставить у из (2.94) в (2.96) и преобразовать полученное выражение, то получим
Совместное решение (2.94) и (2.97) дает точку «возврата» e(fi), т. е. точку огибающей, в которой в момент времени ti изменяется направление движения точек огибающей. Координаты точки «самопересечения» z(t3) —наивысшей точки профиля обработанной поверхности, в которой в момент времени i3 пересекаются траектории движения точек огибающей, вычисляют исходя из следующих условий:
х(*а) = х(г), У(Ы = У(т),
где т — предшествующий момент времени. Точка «минимума огибающей» — точка ц (/4), ордината которой в момент времени ti минимальна. При 0<t<t точка движется по огибающей вправо вверх, при ti<t<t3 — из точки возврата влево вниз, при этом касательная поворачивается по часовой стрелке и этот участок огибающей лежит ниже первого участка. Фактическая дуга контакта шлифовального круга в момент времени і заключена между точками пересечения образующей круга с обрабатываемой поверхностью и с огибающей семейства дуг, образованной в предшествующий момент времени т.
Из рис. 2.12 видно, что возможны два случая.
1. Точка возврата є расположена ниже обрабатываемой поверхности, т. е.
y{tx)<L,
где у (ti) — ордината точки возврата огибающей шлифовального крута; L — ордината обрабатываемой поверхности.
В момент времени t, ti<l<h, когда огибающая образует петлю, координаты точки А определяются уравнениями (2.94), координаты точки В — уравнениями (2.95). Момент времени т, в который образована точка огибающей В, определяется из условий
 |
 |
 |
(хв = х(т), (Ув = у (т),
Одновременно точка В принадлежит образующей шлифовального круга в момент времени т, поэтому ее координаты должны удовлетворять уравнению образующей:
[х (т) — xAf — — Ь [у (т) — ул]‘г = Rz. (2.99)
При совместном решении уравнений (2.98) и (2.99) определяются численные значения т и координаты точки В. Координаты точки С находят исходя из того, что она является точкой образующей шлифовального круга и обрабатываемой поверхности, т. е. должна удовлетворять уравнениям
(Ус — хаТ + (l~ У л)2 = Я2- 1 Ус = У
где хс = УR2 — (L — yAf + хА; ус = L.
Длина фактической дуги контакта шлифовального круга и обрабатываемой детали:
wCB = /?cp, (2.101)
<p = arccos-^-, (2.102)
р = (АС, АВ) = (ха — хА)(хв — хА) + (ус — уА)(ув — уА).
(2.103)
Подставив в выражение (2.101) соответствующие значения и сделав преобразования, получим фактическую длину дуги контакта шлифовального круга и обрабатываемой детали:
у-/СВ = R arc cos (([У К2— (L — R + a cos соtf X
 |
 |
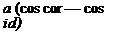
+ j [L — (jR — a + a cos coi)]
Аналогично определяется длина фактической дуги контакта шлифовального круга и обрабатываемой детали и на других участках огибающей траектории шлифовального круга.
2. Точка возврата є (Л) лежит выше обрабатываемой поверхности: y{t)>Lx. В этом случае существует момент времени, когда образующая шлифовального круга пересекает огибающую семейства дуг образующей шлифовального круга, не имея контакта с обрабатываемой деталью, т. е. круг «режет» воздух.
Очевидно, что длина фактической дуги контакта круга с деталью на участке, где точка пересечения его в Момент t с огибающей дуг, образованной в предшествующий момент времени т, не выходящей за пределы обрабатываемой поверхности, соответствует первому случаю (y(tx)<Lx) и рассчитывается по приведенным выше формулам. Различие возможно в том случае, когда траектория шлифовального круга пересекает огибающую выше поверхности обрабатываемой детали, т. е. y(tx)> >Ly.
 |
 |
Ордината точек пересечения огибающей траектории шлифовального круга с обрабатываемой поверхностью должна удовлетворять условию
Исходя из (2.105) и (2.94), можно найти моменты Ті и т2 и абсциссы точек пересечения огибающей траектории шлифовального круга с обрабатываемой поверхностью.
В интервале х(т2) <хс(/)<х(т1) при у (т2) ^ b, y(ta)^s ^ Lx образующая шлифовального круга не имеет дуги контакта с обрабатываемой деталью. В интервале к (та) > xc(t) при у (t) ^ Lx длина дуги контакта траектории шлифовал ь-
Г>. Зак. 1257
ного круга с обрабатываемой деталью рассчитывается по формуле (2.104).
 |
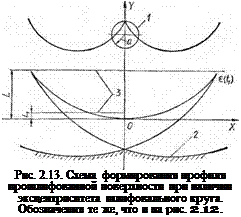Формирование профиля обрабатываемой поверхности при шлифовании кругом, имеющим эксцентриситет относительно оси вращения (рис. 2.13), рассмотрено в работе [25], где даны формулы для определения его координат. Нетрудно заметить, что эти формулы соответствуют уравнению (2.92), если за эксцентриситет принять
амплитуду относительных колебаний оси круга и детали. Тогда уравнения движения центра шлифовального круга имеют вид
хА = vt ± a sin oil,
УА — R — a f a cos оі,
где со — угловая частота, совпадающая с частотой вращения шлифовального круга; а — эксцентриситет шлифовального круга относительно оси его вращения.
Знак <<±» показывает направление вращения шлифовального круга. Уравнения огибающей траектории шлифовального крута, соответствующие уравнениям движения центра (2.106), имеют вид
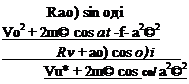х0 = vt ± a sin со?——
Уо — R — а -(- a cos ©f
Несмотря на другой закон движения центра круга, качественная картина образования профиля поверхности обрабатываемой детали сохраняется. Поэтому формулы для расчета характерных точек огибающей траектории шлифовального круга и фактической дуги контакта выводятся из тех же отношений.
Условие возникновения петли огибающей траектории шлифовального круга
где Д^кр — время, за которое шлифовальный круг делает один оборот, a F(t) определяется по формулам (2.112)— (2.120).
Выражения для вычисления фактических характеристик процесса шлифования носят трансцендентный характер и решаются численными методами на ЭВМ.