СОСТАВЛЕНИЕ РАСЧЕТНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

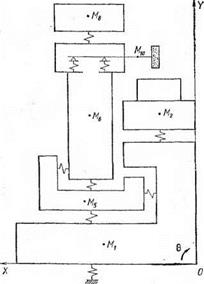
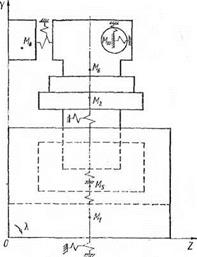
Основой для составления расчетной математической модели, описывающей динамическую систему станка, явились результаты стендовых испытаний виброактивно­сти его отдельных узлов. Анализ экспериментальных дан­ных и технической документации позволил представить динамическую систему станка в виде шестимассовой модели, показанной на рис. 2.6, 2.7.

Передаточная функция упругой системы станка рассматривается как взаимосвязь действующих сил и перемещений в зоне резания. Колебания измеряются в

направлении, перпендикулярном к обрабатываемой по­верхности детали.

Механическая модель представлена в виде отдельных сосредоточенных масс, соединенных жесткостями и об­ладающих определенным демпфированием колебаний. Исходя из пространственной модели, каждое тело обла­дает шестью степенями свободы, т. е. возможностью сме­щения относительно соседних тел по координатам X, Y, Z и углам поворота Я, ц, 0 соответственно вокруг этих осей.

Для сокращения возможного числа степеней свобо­ды, сокращения порядка системы уравнений и упроще­ния схемы многие связи между соседними телами счи­таются жесткими в тех случаях, если ожидаемое пере­мещение по ним либо незначительное, либо мало влияет на относительное вертикальное смещение шпинделя со шлифовальным кругом и стола.

Исходя из этого, были выбраны 18 степеней свободы, представленных в табл. 2.1.

Для каждой из масс в соответствии с расчетной ди­намической моделью (рис. 2.6, 2.7) составлены расчетные схемы и получены аналитические выражения, отражаю­щие ее взаимодействие с соседними массами в общей мо­дели станка.

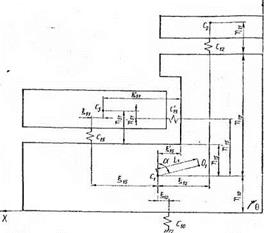
На рис. 2.8, 2.9 в качестве примера представлены рас­четные схемы станины в плоскостях XOY и YOZ.

Приведем метод описания колебаний дифференциаль­ными уравнениями. Кинетическая энергия станины

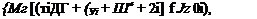т = (All fCnA)2 + ІУх + Ш2 + 2іЗ +

Dy —- Mi (t/i — j- Ii6j),

Dz = MiZi,

Db = Мг [4 i6j — f- ІУі + 2|0[)] 4- Jz Oi. —

Потенциальные энергии стыков

я15= — і — [с^6 (.%+ІівЄі — y5f+czls г+сР1ъ 02 + cjf 02], (2.24)

/С

І7и=4- И; (?Л +ЬА ~ У2)г + б12 (Zl-z2)2-K°2 02]. (2.25)

2

На станину действует обобщенная сила Fx = (0, /у, 0).

Рис. 2.7. Расчетная динамическая схема универсально-заточного станка мод. ЗМ642Е в плоскости YOZ

Использовав уравнения Лагранжа и полученные вы­ше соотношения, запишем уравнения движения для

1-й массы:

ті (У і + SA) + сн) (Уі + SuA) + 6’Yg (.Уі ~Ь Sis®i — Уь) +

"і — сТг (Уі + Si2®i — У2) ~Ь ha (Уі + ЬобО “Ь Мб (Уі — Si501 —

— У б) + {Уі + Si2®r—" Угі ~ 0> (2.26)

miZi + cf02! + cbzx + cf2 (zx — za) — f ftf0Zx — ftf5Zi +

+ hi2 {Zi — 2a) = Fc, (2.27)

[Чі^і + Si (*/i 4- SA)]— J z 0i + SiocS0 (Уі Ію®і) +

Узел	*	Y	*	Я	u	e
Станина и основание стола (1)		Ух	*1			elf
Стол (2)	—	Уі	га	— —	—	■—
Каретка (5)	—	Уа	—	—	—	•—
Колонна со шлифовальной
бабкой (6)	—	Уе		Kg	—.	ee
Электродвигатель привода				e8
шпинделя (8)	—	Уа	*8	Ks	—.
Шпиндель со шлифовальным						010
кругом (10)		Ухо	210		Р10

+ {Уі + Еівбі — Уь) + Ііг^Уг (Уі + ^12®1 Уа) +

(2.28)

+ Ьв^Гв {Уі+ЬА) + іі5—/іТб (уі+ьА й)+

+ £12^12 (Уі + |і20і — Уя) + (сіо + с% + Сіь + С12) 0г — j-

+ (^10 + ^5 + /ііб + ^2) 0 = 0.

Здесь т), І с индексами — координаты расположения со­ответствующих стыков относительно центров жесткости (г| — по оси OY, | — по оси ОХ); первый индекс при них

обозначает центр жесткости, второй — номер сопрягае­мой массы; т] и | с одним индексом — координаты центра жесткости относительно центра массы; Jz — момент инерции относительно оси OZ; Fc — усилие подачи; ту — масса.

где М, С, Я, Л, Лт — матрицы соответственно инерцион­ная, жесткости и демпфирования системы, координатная и транспонированная.

Аналогично получены уравнения движения остальных масс динамической системы станка. В общем виде урав­нения, описывающие относительные колебания шпинде­ля со шлифовальным кругом и стола, будут иметь вид

В рассмотренной схеме внешнее воздействие на си­стему упрощено и в результате правки шлифовальный круг приобретает эксцентриситет. Когда внешние воз­действия на динамическую систему различны и описы­ваются более сложными законами, колебания оси круга и линии контакта его образующей с деталью описыва­ются также более сложными законами, но механизм появления данных колебаний остается таким же, как и в рассмотренном случае. В режиме правки колебания условной линии контакта образующей круга с деталью отсутствуют, а в режиме шлифования они равны разно­сти колебаний оси шлифовального круга относительно обрабатываемой детали в режимах правки и шлифова­ния.