РАСЧЕТНЫЕ СООТНОШЕНИЯ ПРИ ОПИСАНИИ ДИНАМИЧЕСКИХ СИСТЕМ СТАНКОВ

При описании процессов функционирования динами­ческих систем станков обычно с целью упрощения разра­батываются плоские модели. Вместе с тем при описании несимметричных конструкций для обеспечения требуе­мой точности расчета необходима разработка простран­ственной модели, более полно отражающей взаимодей­ствия отдельных систем станка.

Колебания элементов станка опишем уравнениями Лагранжа:

В качестве обобщенных координат gi выберем Хі, у і, Zi> — перемещения при поступательном движении цент­ров жесткости элементов станка, или, что то же самое, центров тяжести элементов относительно положения рав­новесия, и p, j, 0і — углы поворотов элементов станка в положительном направлении относительно осей СХ, CY, CZ правой системы координат, расположенной в
центре жесткости. Кинетическая энергия системы Т рав­на сумме кинетических энергий элементов:

т = 2 Т, = |](7м + т.,)= 2 ).

(2.2)

Здесь Тоі ‘— кинетическая энергия поступательного движе­ния элемента; Т(ЛІ — кинетическая энергия вращательного движения элемента вокруг его центра масс; щ—масса эле­мента; vQi >— абсолютная поступательная скорость центра масс О элемента; JQl ■— момент инерции элемента относи­тельно оси вращения его, проходящей через центр масс; o)j — угловая скорость вращения элемента относительно этой оси.

Потенциальная энергия П упругой системы подсчи­тывается как сумма энергий соответствующих пружин. При этом пружиной заменяется или сама масса, или со­ответствующий стык. Если Л{ — смещение t-й пружины, с{, — соответствующая ей жесткость, то

Я = 4-2МЛг)[3]. (2.3)

Диссипативная функция задается выражением

ф= 4-2МЛ*)2> (2.4)

І

где ht’— коэффициент демпфирования соответствующего стыка.

Обозначим координаты центра жесткости элемента че­рез С{хс, ус, zc), центра тяжести—через О(х0, у0, z0) (ин­декс і опускаем) и положим

б : — (б^., 6у, 6^) = (х§ хс, у0г ус, z0 — zc). (2.5)

Если система координат расположена в центре жестко­сти элемента, то б — радиус-вектор центра тяжести.

Приведем формулы для вычисления координат цент­ра тяжести элемента:

Здесь т — масса элемента; mh — массы составляющих частей элемента; xh, yh, zh — их координаты.

Моменты инерции элемента относительно осей ОХ, OY, OZ задаются формулами

Jx = 2 т* + 4)’ Jy = 2 (xl +

k ft

Jz^rnh{xi + yl), (2-7)

ft

а моменты инерции относительно координатных плоскостей соответственно равны

^XY tftkXhUhi ^YZ ftlhtlhZh, ^XZ

h ft ft

(2.8)

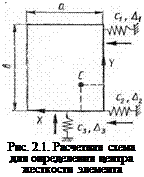
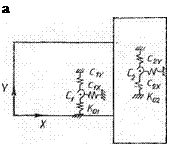
Рассмотрим пример определения координат центра жесткости элемента, имеющего стыки, изображенные на — рис. 2.1.

Пусть Ai, Д2, Дз — перемещения стыков; а и b — гео­метрические размеры элемента. Составим уравнение мо­ментов сил относительно центра жесткости С:

cAi ф — Ус) — с2Д2</е — с3Д3 (а/2 — хс) = 0.

Полагая Ді = Д2 = 0, получаем хс = а!2, а при Лі = Д2,

А3 = 0(/с = сф/фі + с2).

Приведем более детализированные формулы для

вычисления кинетической и потенциальной энергий элементов.

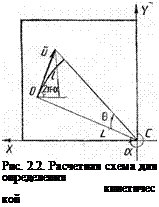
Случай плоского движения. На схеме для определения кинетической энергии (рис. 2.2) 0—угол поворота элемен­та, а—угол между осью CY и вектором б = СО, отсчи­тываемый по часовой стрелке, т. е. в положительном на­правлении согласно правой системе координат CXYZ. Пусть о = (х, у) —скорость центра масс при плоскопараллельном, движении, и — (их, Uy) — скорость при вращении относи­тельно центра жесткости С. Тогда длина дуги I — L0, и— = І = L0, их — — и cos а = — L0 cos а = —6у0, иу =

= —и sin а = —L0 sin а =6×0 и скорость центра масс

У -f — и = (х — 6у0, у + бх0).

Кинетическая энергия

т= -^-т|у + и|2 + -~-/0®2 =

= — L {гп [(.к — бу0)2 + (у + 6Х0)21 + /о02}. (2.9)

На рис. 2.3. приведены схемы для определения потен­циальной энергии элементов, соответствующие двум раз­личным случаям.

Для упругой массы и жесткого стыка (рис. 2.3, а) вво­дится крутильная жесткость Лог, соответствующая углу поворота вокруг центра жесткости Ct. Если смещение меж­ду центрами жесткостей Сь С2 равно I, то деформация

ІС

первой массы будет А і у —— — —- , а второй Д2Х —

С1Х + С2Х

tclx

= —•—:—— . Так как / = х2 — хъ то

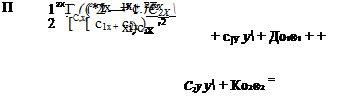С1Х + С2Х

(х2 — Xj)2 + clYy + (2.10)

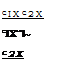
+ с„1% + КаЩ + КюЩ.

На рис. 2.3, б, изображающем жесткую массу и упру­гий стык, через gij, т)ц обозначены координаты /-го стыка I и II пружин:

Ах = t/i — J — £п01, Д2 — Х — Х2— %2®1— ТІ22021

а потенциальная энергия стыков

п = [сп (//іЧ-|п6,і)аЧ-С2х(х. г-х2 — Г]і20і—1>2202)2]. (2.11)

Случай пространственного движения. В общем случае кинетическая энергия вращения вокруг масс задается формулой

Та= ~~ (Jxa> х + JY*l + JZ*-2/xyc°xcoy —

2^угС0у0^х 2J g (2.12)

где сох, соу, a>z— угловые скорости при вращении вокруг осей OX, OY, OZ, а моменты инерции подсчитываются относительно системы координат, помещенной в центр тя­жести и при вращении элемента вокруг центра жесткости на

Рис. 2.3. Расчетная схема для определения потенциальной энергии: а — упругая масса, жесткий стык; б — жесткая масса, упругий стык
перемещения, соответствующие вращениям вокруг коорди­натных осей и — щ — J — щ, щ, из рис. 2.4 получаем

«і = ГіХ, «2 = г2р, «8 = га0;

«їх = 0, «іу = — 8zK uiz — 6yh;

U2X = бх Р, «2Г == о, W22 = — бхр;

«ЗХ = — бу 0, Ызу = бх 6, «32 — О-

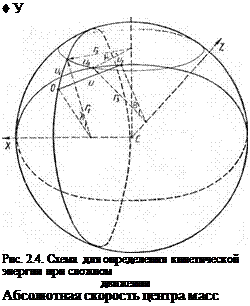Здесь Шх, Шу, Шг—проекции перемещения щ на соответ­ствующие координатные оси, а бх, 6у, бх— координаты радиус-вектора центра тяжести.

V — J — и — (х — j — бх Р — 6у 0, у — бх X — f — 6×0, 2 — f- бу % — бхр).

(2.13)

Из (2.2), (2.12) и (2.13) находим кинетическую энергию Т = —{ш [(х — J — бх р — бу б)2 + (у — бх ^ + бх©)2 +

+ (z + 6y X — 8x P)21 + — W + + Jz№ —

— 2Jxy%li — 2/yzp0 — 2/ zx6X} • (2-14)

В частном случае если р = 0, то

Т = ——- {ш [(х — 8у 0)а + (у — 8z Я + 8х0)2 + (z + Sy X)2]-}-
+ /xX2 + /z02 — 2УмвХ>,

‘ Г = — {т [(х —110)2 + (у — фХ + £0)2 + (г + їіХ)2] +

2

f — JхХ2 + Jz 02 — 2J2x0 X},

где (|, г], я};)- — относительные координаты центра тяже­сти. В частности, если центр жесткости совпадает с цент­ром тяжести, то для плоскопараллельного движения

(2.16)

Потенциальную энергию для элемента со стыками в пространстве можно вычислить, рассматривая схему, изображенную на рис. 2.5. Найдем смещения в стыках, расположенных вдоль координатных осей. Если |, rj, я];— относительные координаты стыка в системе координат, связанной с центром жесткости элемента, то

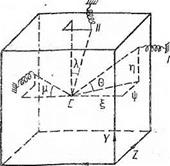‘Ах = X + фр — Г|0,

Ду = у — фХ + к, Az = z + т)Х — £р.

(2.17)

Введя векторы-столбцы

Рис. 2.5. Схема ‘ для определе­ния потенциальной энергии для элемента в пространстве

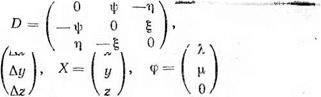и матрицу координат

уравнения (2.17) можно записать в матричном виде

В дальнейшем при разработке динамической модели универсально-заточных станков будут использованы сле­дующие обозначения. Стыки между і-й и /-й массами обоз­начим через Кц. Это обозначение симметрично, т. е. Кц= = Кц. Пусть йц = (іід rj^-, ф^)—векторы относительных координат стыка, очевидно, йцфйн. Через cxlp cf., cf. обозначим линейные, а через с., cf., с?. —угловые жест­кости стыков, tij, h’i/, hij, h%, h%, h% — соответственно демпфирования в стыке Кц. Через Tt обозначим кинетиче­скую энергию і-й массы, Пи и Фц — — соответственно потен­циальная энергия и диссипативная функция стыка Кц.

Связь между с и h приближенно может быть установлена выражением

h = — Ї-Vmc, (2.21)

2зт

где — относительное рассеяние энергии в стыке.